Nic nie może przecież wiecznie trwać»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Nic nie może przecież wiecznie trwać
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 1 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Mamy dany wielokąt wklęsły. Ruch polega na wyborze przekątnej 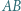 leżącej na zewnątrz tego wielokąta, przy czym cały wielokąt poza punktami
leżącej na zewnątrz tego wielokąta, przy czym cały wielokąt poza punktami 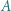 i
i 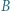 musi leżeć po jednej stronie prostej
musi leżeć po jednej stronie prostej 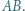 Następnie jedną z łamanych, na które punkty
Następnie jedną z łamanych, na które punkty 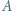 i
i 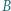 dzielą brzeg wielokąta, odbijamy środkowosymetrycznie względem środka odcinka
dzielą brzeg wielokąta, odbijamy środkowosymetrycznie względem środka odcinka 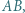 otrzymując nowy wielokąt. Dowieść, że po pewnej, skończonej liczbie takich operacji, otrzymamy wielokąt wypukły.
otrzymując nowy wielokąt. Dowieść, że po pewnej, skończonej liczbie takich operacji, otrzymamy wielokąt wypukły.
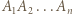 rozważmy wektory
rozważmy wektory 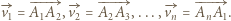 Wykonanie ruchu zmienia jedynie kolejność wektorów
Wykonanie ruchu zmienia jedynie kolejność wektorów 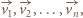 a ta jednoznacznie określa pole wielokąta.
a ta jednoznacznie określa pole wielokąta. i zastępujemy je liczbami
i zastępujemy je liczbami  i
i 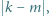 a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.
a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.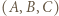 zapiszemy w postaci
zapiszemy w postaci 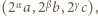 w której
w której 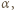
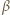 i
i 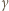 są całkowite nieujemne, zaś
są całkowite nieujemne, zaś 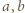 i
i  są nieparzyste lub równe
są nieparzyste lub równe 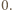 Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki
Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki 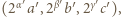 w której
w której 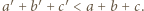 W tym celu przydatne są równości
W tym celu przydatne są równości 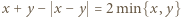 i
i 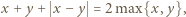 dzięki którym z trójki
dzięki którym z trójki 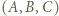 otrzymamy trójkę
otrzymamy trójkę 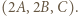
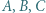 i
i 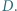 Punkty
Punkty 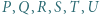 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 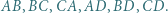 Dowieść, że odcinki
Dowieść, że odcinki 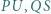 i
i 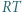 mają wspólny punkt.
mają wspólny punkt.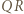 i
i 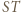 są równoległe do
są równoległe do 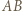 i mają długość
i mają długość 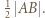 Wynika z tego, że albo punkty
Wynika z tego, że albo punkty 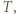
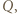
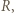
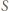 leżą na jednej prostej, albo wyznaczają równoległobok. Analogicznie jest dla odcinków
leżą na jednej prostej, albo wyznaczają równoległobok. Analogicznie jest dla odcinków 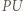 i
i 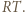
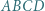 jest wypukły. Punkty
jest wypukły. Punkty 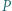 i
i 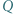 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 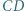 i
i 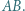 Wykazać, że jeśli
Wykazać, że jeśli 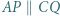 i
i 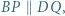 to czworokąt
to czworokąt 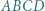 jest równoległobokiem.
jest równoległobokiem.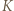 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 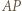 i
i 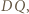 natomiast
natomiast 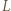 - odcinków
- odcinków 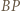 i
i 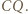 Trójkąty
Trójkąty 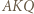 i
i 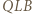 są podobne do trójkąta
są podobne do trójkąta 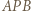 w skali
w skali 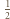 (kbk), a trójkąt
(kbk), a trójkąt 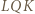 jest do nich przystający (bkb). W takim razie
jest do nich przystający (bkb). W takim razie 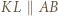 i
i 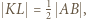 analogicznie
analogicznie 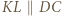 i
i 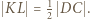
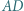 i
i 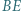 są wysokościami trójkąta
są wysokościami trójkąta 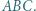 Punkt
Punkt 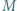 jest środkiem odcinka
jest środkiem odcinka 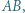 a punkty
a punkty 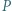 i
i 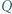 są symetryczne do
są symetryczne do 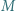 względem prostych odpowiednio
względem prostych odpowiednio 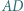 i
i 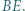 Wykazać, że środek odcinka
Wykazać, że środek odcinka 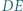 leży na prostej
leży na prostej 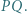
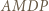 i
i 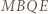 są rombami, bo ich przekątne dzielą się na połowy i są prostopadłe. Odcinki
są rombami, bo ich przekątne dzielą się na połowy i są prostopadłe. Odcinki 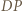 i
i 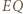 mają zatem długość
mają zatem długość 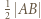 i są równoległe do
i są równoległe do 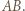
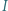 wpisany w trójkąt
wpisany w trójkąt 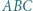 jest styczny do odcinków
jest styczny do odcinków 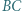 i
i 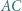 w punktach odpowiednio
w punktach odpowiednio 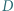 i
i 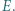 Punkt
Punkt 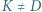 leży na prostej
leży na prostej 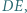 przy czym
przy czym 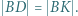 Dowieść, że prosta
Dowieść, że prosta 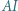 przechodzi przez środek odcinka
przechodzi przez środek odcinka 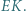
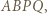 którego przekątna
którego przekątna 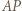 leży na prostej
leży na prostej 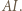 Punkt
Punkt 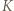 leży na odcinku
leży na odcinku 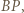 a ponadto
a ponadto 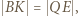 więc czworokąt
więc czworokąt 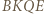 jest równoległobokiem. Z tego wynika, że środek odcinka
jest równoległobokiem. Z tego wynika, że środek odcinka 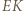 pokrywa się ze środkiem rombu
pokrywa się ze środkiem rombu 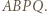
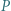 leży wewnątrz trójkąta
leży wewnątrz trójkąta 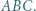 Punkty
Punkty 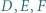 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 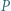 na proste odpowiednio
na proste odpowiednio 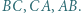 Punkty
Punkty 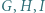 są ortocentrami trójkątów odpowiednio
są ortocentrami trójkątów odpowiednio 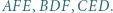 Dowieść, że trójkąty
Dowieść, że trójkąty 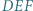 i
i 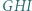 są przystające.
są przystające.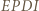 i
i 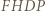 są równoległobokami, gdyż mają po dwie pary boków równoległych, więc czworokąt
są równoległobokami, gdyż mają po dwie pary boków równoległych, więc czworokąt 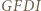 też jest równoległobokiem. Z tego wynika, że
też jest równoległobokiem. Z tego wynika, że 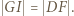 Analogicznie
Analogicznie 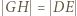 i
i 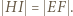
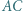 trójkąta
trójkąta 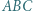 wybrano punkt
wybrano punkt 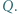 Punkt
Punkt 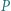 jest środkiem odcinka
jest środkiem odcinka 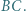 Odcinki
Odcinki 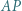 i
i 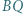 przecinają się w punkcie
przecinają się w punkcie 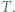 Punkt
Punkt 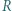 jest środkiem odcinka
jest środkiem odcinka 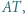 natomiast punkt
natomiast punkt 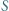 leży na odcinku
leży na odcinku 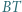 i spełnia równość
i spełnia równość 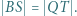 Dowieść, że prosta
Dowieść, że prosta 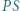 jest równoległa do prostej
jest równoległa do prostej 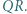
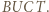 Czworokąt
Czworokąt 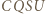 też jest równoległobokiem, czyli
też jest równoległobokiem, czyli 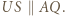 Na koniec
Na koniec 
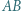 będzie krótszym łukiem okręgu
będzie krótszym łukiem okręgu 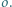 Na łuku
Na łuku 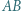 wybieramy punkt
wybieramy punkt 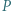 różny od
różny od 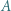 i
i 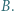 Punkt
Punkt 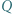 leży na prostej
leży na prostej 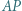 i spełnia równość
i spełnia równość 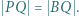 Punkt
Punkt 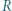 leży na prostej
leży na prostej 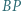 i spełnia warunek
i spełnia warunek 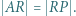 Wreszcie punkt
Wreszcie punkt 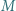 jest środkiem odcinka
jest środkiem odcinka 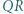 i przez
i przez 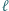 oznaczamy prostą
oznaczamy prostą 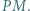 Dowieść, że wszystkie otrzymane w ten sposób proste
Dowieść, że wszystkie otrzymane w ten sposób proste 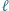 (dla różnych punktów
(dla różnych punktów 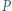 ) mają punkt wspólny.
) mają punkt wspólny. Jest oczywiste, że prosta
Jest oczywiste, że prosta 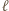 przechodzi przez punkt
przechodzi przez punkt 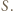 Okrąg opisany na trójkącie
Okrąg opisany na trójkącie 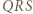 przechodzi przez punkty
przechodzi przez punkty 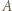 i
i 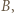 ponadto
ponadto 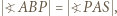 więc prosta
więc prosta 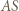 jest styczna do okręgu
jest styczna do okręgu 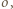 analogicznie prosta
analogicznie prosta 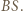 Położenie punktu
Położenie punktu 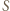 nie zależy zatem od wyboru punktu
nie zależy zatem od wyboru punktu 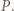
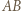 będzie jednym z boków wielokąta środkowosymetrycznego
będzie jednym z boków wielokąta środkowosymetrycznego 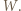 Przez
Przez 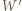 oznaczmy wielokąt
oznaczmy wielokąt 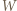 przesunięty o wektor
przesunięty o wektor 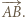 Wówczas wielokąt
Wówczas wielokąt 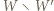 łatwo rozciąć na równoległoboki, a wielokąt
łatwo rozciąć na równoległoboki, a wielokąt 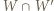 ma środek symetrii i o dwa boki mniej niż wielokąt
ma środek symetrii i o dwa boki mniej niż wielokąt 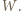
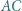 trójkąta prostokątnego
trójkąta prostokątnego 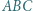 został dowolnie wybrany punkt
został dowolnie wybrany punkt 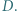 Symetralna odcinka
Symetralna odcinka 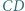 przecina przeciwprostokątną
przecina przeciwprostokątną 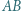 w punkcie
w punkcie 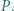 Punkt
Punkt 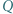 jest symetryczny do
jest symetryczny do 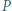 względem środka
względem środka 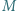 odcinka
odcinka 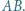 Punkt
Punkt 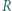 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu 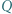 na prostą
na prostą 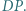 Udowodnić, że
Udowodnić, że 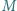 leży na dwusiecznej kąta
leży na dwusiecznej kąta 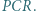
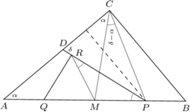
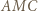 i
i 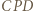 są równoramienne. Przyjmijmy oznaczenia:
są równoramienne. Przyjmijmy oznaczenia: 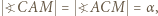
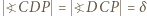 ; zatem
; zatem 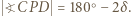 Środek odcinka
Środek odcinka 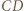 leży bliżej punktu
leży bliżej punktu 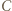 niż punktu
niż punktu 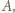 wobec czego punkt
wobec czego punkt 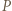 leży między
leży między 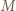 i
i 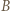 ; w takim razie
; w takim razie 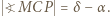 Rachunek kątów w trójkącie
Rachunek kątów w trójkącie 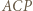 pokazuje, że
pokazuje, że 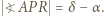
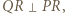 trójkąt
trójkąt 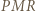 jest równoramienny, więc
jest równoramienny, więc 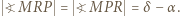 Uzyskujemy równość
Uzyskujemy równość 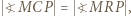 z której wynika, że czworokąt
z której wynika, że czworokąt 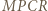 ma okrąg opisany. Skoro
ma okrąg opisany. Skoro 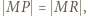 punkt
punkt 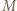 jest środkiem łuku
jest środkiem łuku 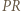 tego okręgu; a to znaczy, że półprosta
tego okręgu; a to znaczy, że półprosta 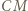 połowi kąt
połowi kąt 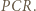 To teza zadania.
To teza zadania.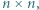 gdzie
gdzie 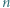 jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem
jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem 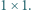 Znaleźć najmniejszą możliwą liczbę kwadratów
Znaleźć najmniejszą możliwą liczbę kwadratów 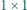 uzyskanych w takim podziale.
uzyskanych w takim podziale.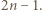
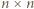 na
na 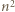 kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest
kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest 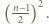
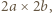 a więc o polu
a więc o polu 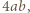 zawiera dokładnie
zawiera dokładnie 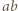 wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej
wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej 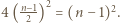 Łączne pole kwadratów jednostkowych jest zatem równe co najmniej
Łączne pole kwadratów jednostkowych jest zatem równe co najmniej 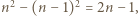 skąd wniosek, że jest co najmniej tyle takich kwadratów.
skąd wniosek, że jest co najmniej tyle takich kwadratów.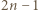 kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku
kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku 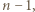 a pozostałą część podzielić na kwadraty jednostkowe.
a pozostałą część podzielić na kwadraty jednostkowe.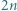 -kąta foremnego oznaczono przez
-kąta foremnego oznaczono przez 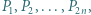 niekoniecznie w tej kolejności. Udowodnić, że łamana zamknięta
niekoniecznie w tej kolejności. Udowodnić, że łamana zamknięta 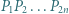 zawiera parę odcinków równoległych.
zawiera parę odcinków równoległych.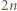 oraz oznaczmy przez
oraz oznaczmy przez 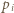 resztę przyporządkowaną wierzchołkowi
resztę przyporządkowaną wierzchołkowi 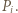
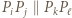 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 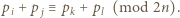 Przypuśćmy nie wprost, że liczby
Przypuśćmy nie wprost, że liczby 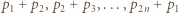 dają parami różne reszty przy dzieleniu przez
dają parami różne reszty przy dzieleniu przez 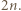 Wówczas ich suma daje resztę
Wówczas ich suma daje resztę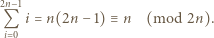
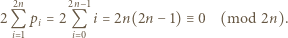
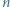 przekątnych
przekątnych 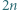 -kąta foremnego przecina się w jednym punkcie, który nie jest wierzchołkiem tego wielokąta. Wykazać, że jest jego środkiem.
-kąta foremnego przecina się w jednym punkcie, który nie jest wierzchołkiem tego wielokąta. Wykazać, że jest jego środkiem.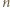 przekątnych. Ponieważ pozostałych
przekątnych. Ponieważ pozostałych 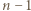 przekątnych ją przecina, więc po obu stronach rozważanej przekątnej znajduje się po
przekątnych ją przecina, więc po obu stronach rozważanej przekątnej znajduje się po 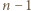 wierzchołków wielokąta. Stąd wniosek, że ta przekątna łączy przeciwległe wierzchołki
wierzchołków wielokąta. Stąd wniosek, że ta przekątna łączy przeciwległe wierzchołki 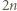 -kąta foremnego, więc przechodzi przez jego środek.
-kąta foremnego, więc przechodzi przez jego środek.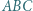 wpisany w okrąg
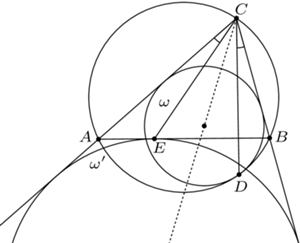
wpisany w okrąg  Okrąg
Okrąg 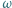 jest styczny do odcinków
jest styczny do odcinków 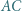 i
i 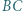 oraz do okręgu
oraz do okręgu  w punkcie
w punkcie 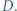 Okrąg
Okrąg 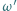 zaś jest dopisany do trójkąta
zaś jest dopisany do trójkąta 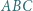 i styczny do boku
i styczny do boku 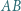 w punkcie
w punkcie 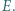 Wykazać, że
Wykazać, że 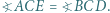
 i promieniu
i promieniu 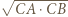 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 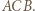 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 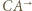 i
i 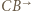 oraz prostą
oraz prostą 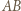 z okręgiem
z okręgiem 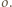 W takim razie okrąg
W takim razie okrąg 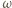 przejdzie na okrąg styczny do prostej
przejdzie na okrąg styczny do prostej 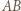 i półprostych
i półprostych 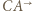 i
i 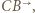 czyli na okrąg
czyli na okrąg 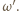 Stąd wniosek, że obrazem punktu
Stąd wniosek, że obrazem punktu 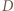 jest punkt
jest punkt 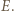 Półprosta
Półprosta 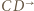 przejdzie więc na półprostą
przejdzie więc na półprostą 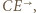 a skoro inwersja zachowuje kąty, to
a skoro inwersja zachowuje kąty, to 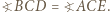
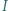 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 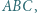 zaś
zaś  jest okręgiem opisanym na tym trójkącie. Okrąg
jest okręgiem opisanym na tym trójkącie. Okrąg 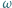 styczny do odcinków
styczny do odcinków 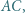
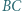 jest styczny do okręgu
jest styczny do okręgu  w punkcie
w punkcie 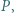 a
a 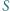 jest środkiem tego łuku
jest środkiem tego łuku 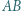 okręgu
okręgu 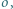 na którym leży punkt
na którym leży punkt 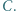 Wykazać, że punkty
Wykazać, że punkty 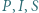 są współliniowe.
są współliniowe.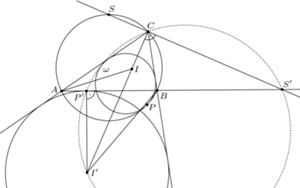
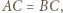 to punkty
to punkty 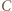 i
i 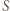 pokrywają się i punkty
pokrywają się i punkty 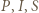 leżą na dwusiecznej
leżą na dwusiecznej 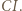 Dalej zakładamy, że
Dalej zakładamy, że 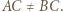 Wówczas punkty
Wówczas punkty 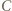 i
i 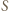 są różne, zaś proste
są różne, zaś proste 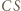 i
i 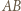 nie są równoległe. Rozważmy złożenie inwersji o środku
nie są równoległe. Rozważmy złożenie inwersji o środku 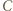 i promieniu
i promieniu 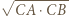 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 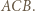 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 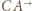 i
i 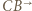 oraz prostą
oraz prostą 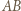 z okręgiem
z okręgiem 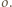 Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu
Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu 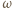 jest okrąg dopisany do trójkąta
jest okrąg dopisany do trójkąta 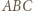 styczny do boku
styczny do boku 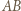 w punkcie
w punkcie 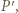 który jest obrazem punktu
który jest obrazem punktu 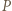 w tym przekształceniu. Ponieważ
w tym przekształceniu. Ponieważ 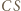 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 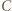 trójkąta
trójkąta 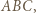 to proste
to proste 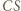 i
i 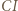 są prostopadłe. W takim razie obrazem punktu
są prostopadłe. W takim razie obrazem punktu 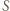 jest punkt
jest punkt 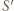 przecięcia prostej
przecięcia prostej 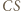 (która jest swoim własnym obrazem) z prostą
(która jest swoim własnym obrazem) z prostą 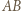 (która jest obrazem okręgu
(która jest obrazem okręgu  ). Niech
). Niech 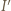 będzie obrazem punktu
będzie obrazem punktu 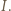 Wtedy z definicji inwersji mamy
Wtedy z definicji inwersji mamy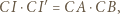
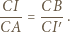
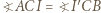 (bo inwersja zachowuje kąty) otrzymujemy, że trójkąty
(bo inwersja zachowuje kąty) otrzymujemy, że trójkąty 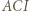 i
i 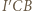 są podobne. W takim razie
są podobne. W takim razie 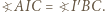 Ponieważ
Ponieważ 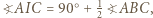 to mamy
to mamy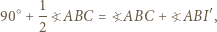
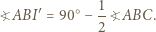
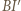 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 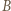 trójkąta
trójkąta 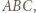 więc
więc 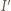 jest środkiem okręgu dopisanego do trójkąta
jest środkiem okręgu dopisanego do trójkąta 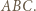 W takim razie
W takim razie 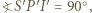 co wraz z równością
co wraz z równością 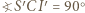 (bo
(bo 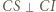 ) oznacza, że punkty
) oznacza, że punkty 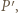
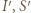 i
i 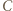 leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty
leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty 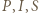 są współliniowe.
są współliniowe.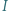 jest wpisany w trójkąt
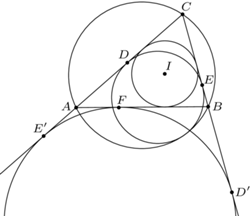
jest wpisany w trójkąt 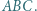 Okrąg
Okrąg 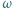 styczny do okręgu opisanego na trójkącie
styczny do okręgu opisanego na trójkącie 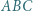 jest styczny do odcinków
jest styczny do odcinków 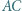 i
i 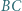 odpowiednio w punktach
odpowiednio w punktach 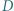 i
i 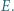 Wykazać, że punkt
Wykazać, że punkt 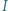 leży na odcinku
leży na odcinku 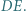
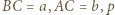 to połowa obwodu trójkąta
to połowa obwodu trójkąta 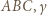 to miara kąta
to miara kąta 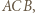 zaś
zaś  to promień okręgu wpisanego w trójkąt
to promień okręgu wpisanego w trójkąt 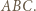 Inwersja o środku
Inwersja o środku 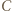 i promieniu
i promieniu 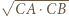 złożona z symetrią względem dwusiecznej kąta
złożona z symetrią względem dwusiecznej kąta 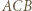 przeprowadza okrąg
przeprowadza okrąg 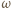 na okrąg dopisany do trójkąta
na okrąg dopisany do trójkąta 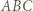 styczny do boku
styczny do boku 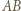 w punkcie
w punkcie 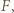 a punkty
a punkty 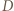 i
i 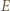 odpowiednio na punkty
odpowiednio na punkty 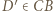 i
i 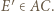 Ponieważ
Ponieważ 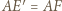 i
i 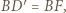 to
to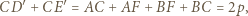
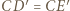 prowadzi do wniosku, że
prowadzi do wniosku, że 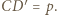 Z drugiej strony z definicji inwersji mamy
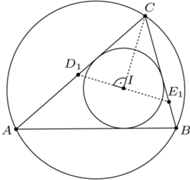
Z drugiej strony z definicji inwersji mamy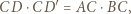
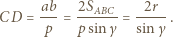
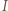 i prostopadła do prostej
i prostopadła do prostej 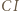 przecina boki
przecina boki 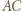 i
i 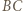 odpowiednio w punktach
odpowiednio w punktach 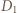 i
i 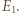 Skoro
Skoro 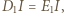 to odległość punktu
to odległość punktu 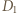 od prostej
od prostej 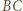 jest równa
jest równa 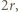 skąd wniosek, że
skąd wniosek, że 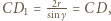 czyli
czyli 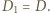 Analogicznie uzasadnimy, że
Analogicznie uzasadnimy, że 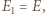 więc punkt
więc punkt 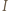 leży na odcinku
leży na odcinku 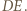
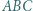 jest wpisany w okrąg
jest wpisany w okrąg 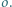 Punkty
Punkty 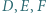 są środkami łuków
są środkami łuków 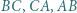 niezawierających pozostałych wierzchołków trójkąta. Punkty
niezawierających pozostałych wierzchołków trójkąta. Punkty 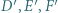 są symetryczne do punktów
są symetryczne do punktów 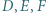 odpowiednio względem boków
odpowiednio względem boków 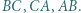 Wykazać, że punkty
Wykazać, że punkty 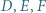 oraz ortocentrum trójkąta
oraz ortocentrum trójkąta 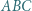 leżą na jednym okręgu.
leżą na jednym okręgu.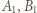 i
i 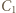 będą spodkami wysokości trójkąta
będą spodkami wysokości trójkąta 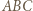 poprowadzonymi odpowiednio z wierzchołków
poprowadzonymi odpowiednio z wierzchołków 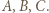 Ponieważ na czworokątach
Ponieważ na czworokątach 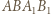 i
i 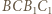 można opisać okręgi, to
można opisać okręgi, to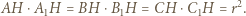
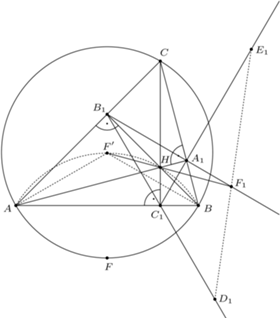
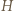 i promieniu
i promieniu  złożoną z symetrią środkową względem punktu
złożoną z symetrią środkową względem punktu 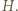 Obrazami punktów
Obrazami punktów 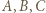 są zatem punkty
są zatem punkty 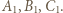 Ponieważ
Ponieważ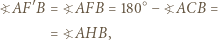
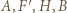 leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą
leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą 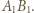 Obrazem punktu
Obrazem punktu 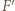 jest punkt
jest punkt 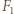 przecięcia prostych
przecięcia prostych 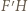 i
i 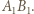 Analogicznie stwierdzamy, że w tym przekształceniu punkt
Analogicznie stwierdzamy, że w tym przekształceniu punkt 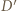 przechodzi na punkt
przechodzi na punkt 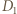 przecięcia prostych
przecięcia prostych 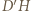 i
i 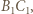 a punkt
a punkt 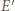 przechodzi na punkt
przechodzi na punkt 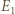 przecięcia prostych
przecięcia prostych 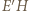 i
i 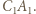
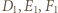 leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta
leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta 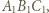 widzimy, że wystarczy wykazać, że
widzimy, że wystarczy wykazać, że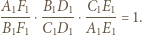
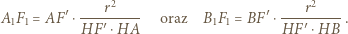
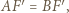 widzimy, że
widzimy, że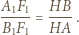

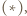 co kończy rozwiązanie.
co kończy rozwiązanie.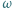 wpisany w trójkąt
wpisany w trójkąt 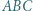 jest styczny do boku
jest styczny do boku 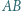 w punkcie
w punkcie 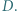 Okrąg
Okrąg 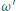 jest styczny do półprostych
jest styczny do półprostych 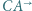 i
i 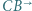 oraz jest styczny zewnętrznie w punkcie
oraz jest styczny zewnętrznie w punkcie 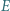 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 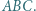 Wykazać, że
Wykazać, że 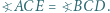
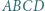 o podstawach
o podstawach 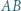 i
i 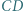 jest wpisany w okrąg
jest wpisany w okrąg 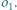 Okrąg
Okrąg 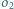 jest styczny do odcinków
jest styczny do odcinków 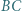 i
i 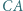 oraz jest styczny wewnętrznie do okręgu
oraz jest styczny wewnętrznie do okręgu 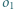 w punkcie
w punkcie 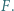 Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt 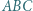 jest styczny do odcinka
jest styczny do odcinka 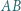 w punkcie
w punkcie 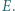 Dowieść, że punkty
Dowieść, że punkty 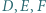 leżą na jednej prostej.
leżą na jednej prostej.