Załóżmy, że trzy elipsy, o których mowa, mają punkt wspólny 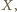 leżący w odległościach
leżący w odległościach 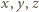 odpowiednio od wierzchołków
odpowiednio od wierzchołków 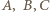 zadanego trójkąta, o bokach długości
zadanego trójkąta, o bokach długości 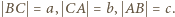 Elipsa o ogniskach
Elipsa o ogniskach 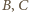 przechodzi przez punkty
przechodzi przez punkty 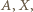 więc
więc 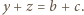 Analogicznie
Analogicznie 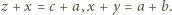 Ten układ równań z niewiadomymi
Ten układ równań z niewiadomymi 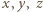 ma jedyne rozwiązanie
ma jedyne rozwiązanie 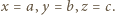 Odległości punktu
Odległości punktu 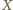 od
od 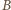 oraz
oraz 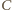 wynoszą więc, odpowiednio,
wynoszą więc, odpowiednio, 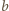 oraz
oraz  - czyli przeciwnie niż odległości punktu
- czyli przeciwnie niż odległości punktu 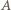 od
od 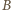 oraz
oraz 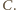 To wyznacza dwa możliwe położenia punktu
To wyznacza dwa możliwe położenia punktu 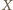 - może to być punkt symetryczny do
- może to być punkt symetryczny do 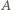 względem symetralnej odcinka
względem symetralnej odcinka 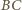 lub punkt symetryczny do
lub punkt symetryczny do 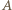 względem środka odcinka
względem środka odcinka 
W pierwszym przypadku punkty 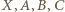 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 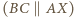 ; w drugim - tworzą równoległobok
; w drugim - tworzą równoległobok 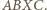 Dodatkowa informacja, że
Dodatkowa informacja, że 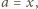 czyli
czyli 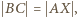 daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt
daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt 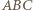 jest prostokątny.
jest prostokątny.
Na odwrót, gdy trójkąt jest prostokątny, wówczas wystarczy go uzupełnić do prostokąta czwartym wierzchołkiem; widać, że ów wierzchołek będzie wspólnym punktem trzech omawianych elips.

 ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
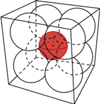
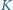 dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 (
dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 ( -wymiarowej kuli
-wymiarowej kuli 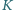 dla
dla  -wymiarowego hipersześcianu o krawędzi 2 i
-wymiarowego hipersześcianu o krawędzi 2 i 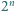 kul
kul 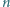 -wymiarowych o średnicy 1.
-wymiarowych o średnicy 1.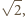 stąd
stąd 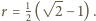
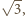 stąd
stąd 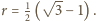
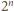 kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość
kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość 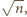 stąd
stąd 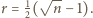
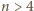 uzyskujemy
uzyskujemy 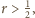 więc "mała" kulka
więc "mała" kulka 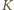 jest większa od każdej z "dużych" kul, a dla
jest większa od każdej z "dużych" kul, a dla 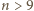 mamy
mamy 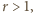 czyli kula
czyli kula  wystaje poza hipersześcian!
wystaje poza hipersześcian!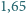 m. Czy istnieje możliwość przesłania fletu?
m. Czy istnieje możliwość przesłania fletu?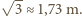


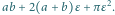

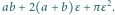
 -otoczkę pudełka o wymiarach
-otoczkę pudełka o wymiarach 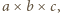 czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż
czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż 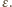 Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest
Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest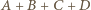
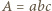 (objętość wyjściowego prostopadłościanu),
(objętość wyjściowego prostopadłościanu),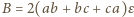 (objętości prostopadłościanów zbudowanych na ścianach),
(objętości prostopadłościanów zbudowanych na ścianach),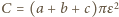 (fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy
(fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy  ),
),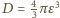 (fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu
(fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu  ).
).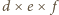 da się włożyć do pudełka o wymiarach
da się włożyć do pudełka o wymiarach 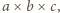 to również
to również  -otoczka pierwszego mieści się w
-otoczka pierwszego mieści się w  -otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna:
-otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna: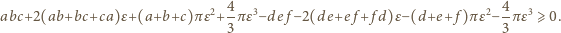
 Skoro ma on wartość nieujemną dla każdego
Skoro ma on wartość nieujemną dla każdego  to musi mieć dodatni współczynnik przy najwyższej potędze
to musi mieć dodatni współczynnik przy najwyższej potędze 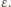 Stąd
Stąd 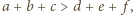 co kończy dowód.
co kończy dowód.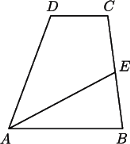
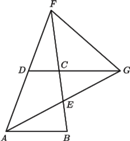
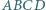 boki
boki 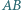 i
i 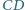 są równoległe oraz
są równoległe oraz 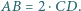 Punkt
Punkt 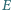 jest środkiem boku
jest środkiem boku 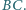 Udowodnić, że jeśli w czworokąt
Udowodnić, że jeśli w czworokąt  można wpisać okrąg, to
można wpisać okrąg, to 
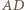 i
i 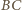 przecinają się w punkcie
przecinają się w punkcie 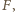 a proste
a proste 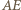 i
i 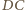 w punkcie
w punkcie 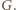
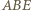 i
i 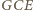 są przystające, a w szczególności
są przystające, a w szczególności 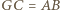 oraz
oraz 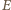 jest środkiem
jest środkiem 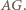 Ponadto
Ponadto 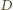 jest środkiem
jest środkiem 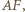 ponieważ odcinek
ponieważ odcinek 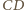 jest równoległy do
jest równoległy do 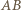 i dwa razy krótszy. Zatem
i dwa razy krótszy. Zatem 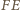 i
i 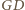 są środkowymi w trójkącie
są środkowymi w trójkącie 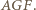
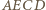 można wpisać okrąg, to zachodzi równość
można wpisać okrąg, to zachodzi równość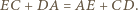
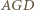 i
i 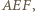 które mają równe pola (równe połowie pola trójkąta
które mają równe pola (równe połowie pola trójkąta 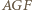 ). W takim razie mają również równe obwody, czyli
). W takim razie mają również równe obwody, czyli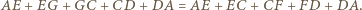
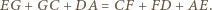
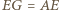 i
i 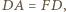 to mamy też
to mamy też 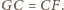 Stąd dostajemy
Stąd dostajemy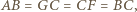

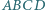 boki
boki 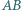 i
i 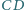 są równoległe oraz
są równoległe oraz 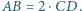 Punkt
Punkt 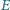 jest środkiem boku
jest środkiem boku 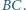 Udowodnić, że jeśli
Udowodnić, że jeśli 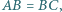 to w czworokąt
to w czworokąt 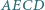 można wpisać okrąg.
można wpisać okrąg.
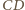 punkt
punkt 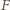 w taki sposób, aby czworokąt
w taki sposób, aby czworokąt 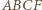 był równoległobokiem.
był równoległobokiem.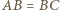 możemy wywnioskować, że
możemy wywnioskować, że 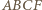 jest rombem. Ponadto, skoro
jest rombem. Ponadto, skoro 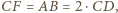 to punkt
to punkt 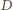 jest środkiem boku
jest środkiem boku 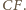 Ponieważ punkt
Ponieważ punkt 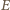 jest środkiem boku
jest środkiem boku 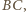 więc punkty
więc punkty 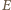 i
i 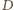 są symetryczne względem prostej
są symetryczne względem prostej 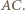 Oznacza to, że czworokąt
Oznacza to, że czworokąt 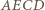 jest deltoidem, zatem w szczególności można w niego wpisać okrąg.
jest deltoidem, zatem w szczególności można w niego wpisać okrąg.
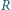 i
i  są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
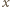 oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach
oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach 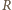 i
i  oraz przyprostokątną o długości
oraz przyprostokątną o długości 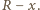 Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa
Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa 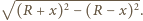
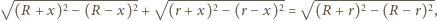
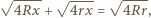
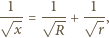
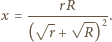
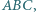 mając dany jego wierzchołek
mając dany jego wierzchołek 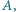 punkt
punkt 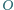 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 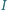 - środek okręgu wpisanego.
- środek okręgu wpisanego.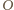 i promieniu
i promieniu 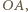
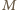 - jego punkt przecięcia z prostą
- jego punkt przecięcia z prostą 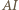 oraz okrąg o środku
oraz okrąg o środku 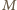 i promieniu
i promieniu 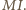 Na mocy twierdzenia
Na mocy twierdzenia 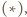 punkty przecięcia powyższych dwóch okręgów to wierzchołki
punkty przecięcia powyższych dwóch okręgów to wierzchołki 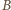 i
i 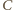 trójkąta.
trójkąta.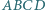 jest wpisany w okrąg
jest wpisany w okrąg 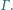 Punkt
Punkt 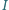 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 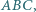 prosta
prosta 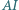 przecina okrąg
przecina okrąg 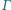 w punkcie
w punkcie 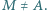 Punkt
Punkt 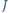 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 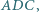 prosta
prosta 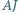 przecina okrąg
przecina okrąg 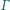 w punkcie
w punkcie 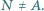 Wykaż, że jeżeli
Wykaż, że jeżeli 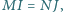 to
to 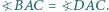
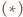 i założenia, zachodzi równość
i założenia, zachodzi równość 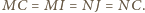 Stąd
Stąd 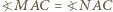 jako kąty wpisane w okrąg
jako kąty wpisane w okrąg 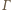 oparte na równych łukach. Wobec tego
oparte na równych łukach. Wobec tego 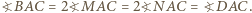
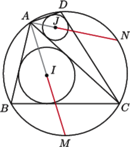
 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt  Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie  wyznacza na prostych
wyznacza na prostych 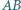 i
i 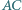 równe cięciwy.
równe cięciwy.
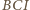 jest punkt
jest punkt 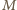 z twierdzenia
z twierdzenia 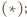 leży on na dwusiecznej kąta
leży on na dwusiecznej kąta 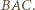 Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.
Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.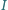 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 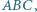 punkt
punkt 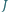 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka  należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 
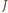 leży w kącie
leży w kącie 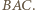 Dwusieczne kątów przyległych są prostopadłe, więc
Dwusieczne kątów przyległych są prostopadłe, więc 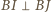 oraz
oraz 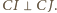 Wobec tego na czworokącie
Wobec tego na czworokącie 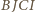 można opisać okrąg, którego środkiem jest środek
można opisać okrąg, którego środkiem jest środek 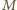 odcinka
odcinka 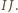 Okrąg ten jest opisany na trójkącie
Okrąg ten jest opisany na trójkącie 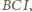 czyli
czyli 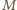 to punkt z twierdzenia
to punkt z twierdzenia 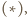 leży więc na okręgu opisanym na trójkącie
leży więc na okręgu opisanym na trójkącie 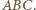
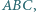 mając dane jego wierzchołki
mając dane jego wierzchołki 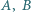 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego. jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 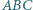 w punkcie
w punkcie 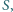 a do boków
a do boków 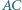 i
i 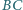 odpowiednio w punktach
odpowiednio w punktach 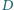 i
i 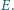 Wykaż, że jeśli
Wykaż, że jeśli 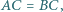 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 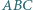 jest środkiem odcinka
jest środkiem odcinka 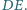
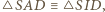 gdzie
gdzie 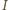 to środek odcinka
to środek odcinka 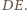

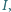 wpisany w trójkąt
wpisany w trójkąt 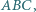 jest styczny do boku
jest styczny do boku 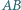 w punkcie
w punkcie 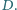 Punkt
Punkt 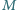 jest środkiem boku
jest środkiem boku 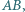 punkt
punkt 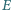 jest symetryczny do punktu
jest symetryczny do punktu 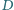 względem
względem 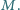 Udowodnić, że proste
Udowodnić, że proste 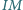 oraz
oraz 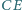 są równoległe.
są równoległe.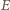 jest punktem styczności z bokiem
jest punktem styczności z bokiem 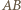 okręgu dopisanego do trójkąta
okręgu dopisanego do trójkąta 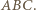 Jeżeli więc przez
Jeżeli więc przez 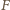 oznaczymy punkt środkowosymetryczny do
oznaczymy punkt środkowosymetryczny do 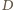 względem
względem 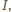 to jednokładność o środku w punkcie
to jednokładność o środku w punkcie 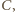 która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt
która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt 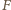 na punkt
na punkt 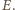 A zatem punkty
A zatem punkty 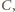
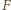 i
i 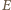 są współliniowe. Prosta
są współliniowe. Prosta 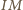 jest zatem prostą łączącą środki boków w trójkącie
jest zatem prostą łączącą środki boków w trójkącie 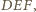 a stąd wynika żądana równoległość.
a stąd wynika żądana równoległość.
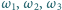 mają wspólny punkt
mają wspólny punkt 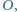 a ponadto
a ponadto 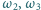 przecinają się jeszcze w punkcie
przecinają się jeszcze w punkcie 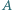 i podobnie
i podobnie 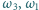 i
i 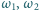 - w punkcie
- w punkcie 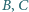 odpowiednio. Prosta
odpowiednio. Prosta 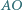 przecina
przecina 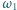 ponadto w punkcie
ponadto w punkcie 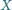 i podobnie
i podobnie 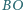 przecina
przecina 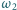 w
w 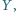 a
a 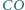 przecina
przecina 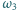 w
w 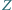 (rysunek). Udowodnić, że
(rysunek). Udowodnić, że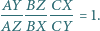
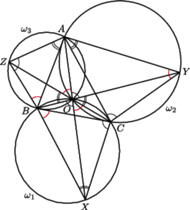
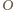 jak następuje:
jak następuje: 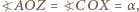
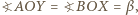
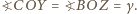
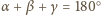 oraz na mocy tw. o kątach wpisanych,
oraz na mocy tw. o kątach wpisanych, 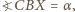
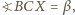 więc kąty w trójkącie
więc kąty w trójkącie 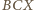 wynoszą
wynoszą 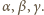 Analogicznie jest dla trójkątów
Analogicznie jest dla trójkątów 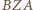 i
i 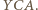 Zatem są to trójkąty podobne do trójkąta
Zatem są to trójkąty podobne do trójkąta 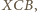 w szczególności
w szczególności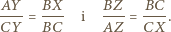
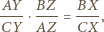

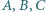 są trzema kolejnymi wierzchołkami pięciokąta foremnego wpisanego w okrąg o promieniu
są trzema kolejnymi wierzchołkami pięciokąta foremnego wpisanego w okrąg o promieniu  Obliczyć
Obliczyć 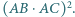

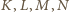 to środki odcinków).
to środki odcinków).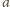 oznacza długość boku pięciokąta oraz
oznacza długość boku pięciokąta oraz 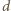 - długość przekątnej. Z podobieństwa trójkątów
- długość przekątnej. Z podobieństwa trójkątów 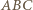 i
i 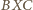 mamy
mamy 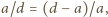 skąd
skąd 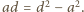 Z podobieństwa trójkątów
Z podobieństwa trójkątów 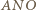 i
i 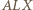 otrzymujemy
otrzymujemy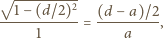
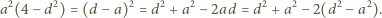
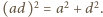 Wreszcie z podobieństwa trójkątów
Wreszcie z podobieństwa trójkątów 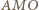 i
i 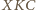 i
i 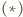 mamy
mamy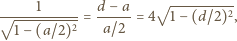
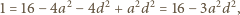
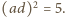
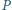 zaznaczono
zaznaczono 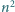 różnych punktów. Dla każdej liczby całkowitej
różnych punktów. Dla każdej liczby całkowitej 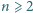 znaleźć największą możliwą liczbę prostokątów, w których każdy wierzchołek jest jednym z zaznaczonych punktów, a boki są równoległe do boków prostokąta
znaleźć największą możliwą liczbę prostokątów, w których każdy wierzchołek jest jednym z zaznaczonych punktów, a boki są równoległe do boków prostokąta 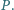
 i
i 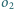 o środkach odpowiednio
o środkach odpowiednio 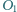 i
i 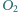 przecinają się w dwóch różnych punktach
przecinają się w dwóch różnych punktach 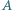 i
i 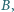 przy czym kąt
przy czym kąt 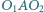 jest rozwarty. Prosta
jest rozwarty. Prosta 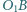 przecina okrąg
przecina okrąg 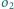 w punkcie
w punkcie 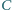 różnym od
różnym od 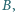 a prosta
a prosta 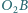 przecina okrąg
przecina okrąg 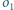 w punkcie
w punkcie 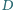 różnym od
różnym od 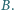 Wykazać, że punkt
Wykazać, że punkt 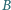 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 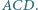
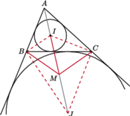
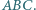 Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt
Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt 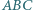 jest prostokątny.
jest prostokątny.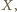 leżący w odległościach
leżący w odległościach 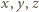 odpowiednio od wierzchołków
odpowiednio od wierzchołków 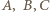 zadanego trójkąta, o bokach długości
zadanego trójkąta, o bokach długości 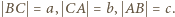 Elipsa o ogniskach
Elipsa o ogniskach 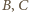 przechodzi przez punkty
przechodzi przez punkty 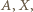 więc
więc 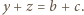 Analogicznie
Analogicznie 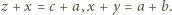 Ten układ równań z niewiadomymi
Ten układ równań z niewiadomymi 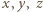 ma jedyne rozwiązanie
ma jedyne rozwiązanie 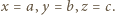 Odległości punktu
Odległości punktu 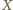 od
od 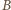 oraz
oraz 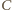 wynoszą więc, odpowiednio,
wynoszą więc, odpowiednio, 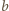 oraz
oraz  - czyli przeciwnie niż odległości punktu
- czyli przeciwnie niż odległości punktu 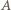 od
od 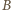 oraz
oraz 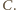 To wyznacza dwa możliwe położenia punktu
To wyznacza dwa możliwe położenia punktu 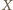 - może to być punkt symetryczny do
- może to być punkt symetryczny do 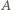 względem symetralnej odcinka
względem symetralnej odcinka 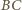 lub punkt symetryczny do
lub punkt symetryczny do 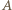 względem środka odcinka
względem środka odcinka 
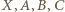 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 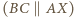 ; w drugim - tworzą równoległobok
; w drugim - tworzą równoległobok 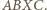 Dodatkowa informacja, że
Dodatkowa informacja, że 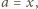 czyli
czyli 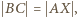 daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt
daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt 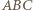 jest prostokątny.
jest prostokątny. licząc od wierzchołka.
licząc od wierzchołka.