Każdy trójkąt jest równoboczny»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Każdy trójkąt jest równoboczny
- Publikacja w Delcie: grudzień 2014
- Publikacja elektroniczna: 01-12-2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Wykaż, że w każdym trapezie o nierównoległych ramionach punkt przecięcia ich przedłużeń, punkt przecięcia przekątnych i środki podstaw leżą na jednej prostej.
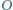 jest środkiem elipsy wpisanej w czworokąt
jest środkiem elipsy wpisanej w czworokąt 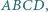 to
to
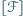 oznacza pole figury
oznacza pole figury 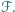
 obrazem punktu
obrazem punktu  jest środek okręgu
jest środek okręgu  Czworokąt
Czworokąt 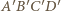 jest opisany na okręgu, zachodzi więc równość
jest opisany na okręgu, zachodzi więc równość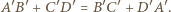
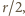 uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.
uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.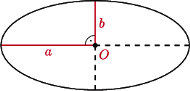
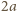 i
i 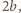 równoległych do jej półosi. Powinowactwo prostokątne o skali
równoległych do jej półosi. Powinowactwo prostokątne o skali 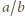 i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola
i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola 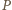 elipsy do pola
elipsy do pola 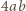 prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli
prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli 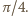 Wobec tego
Wobec tego 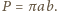
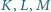 leżą odpowiednio na bokach
leżą odpowiednio na bokach 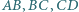 równoległoboku
równoległoboku 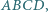 przy czym
przy czym
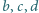 przechodzą odpowiednio przez punkty
przechodzą odpowiednio przez punkty 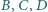 oraz są równoległe odpowiednio do prostych
oraz są równoległe odpowiednio do prostych 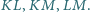 Udowodnij, że proste
Udowodnij, że proste 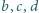 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.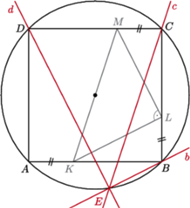
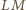 powstaje z odcinka
powstaje z odcinka 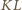 przez obrót o
przez obrót o 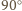 wokół środka kwadratu, zatem
wokół środka kwadratu, zatem 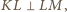 więc także
więc także 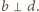 Stąd punkt
Stąd punkt 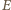 przecięcia prostych
przecięcia prostych 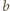 i
i 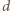 leży na okręgu opisanym na kwadracie. Ponadto skoro
leży na okręgu opisanym na kwadracie. Ponadto skoro 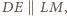 to punkt
to punkt 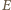 musi należeć do tego łuku
musi należeć do tego łuku 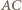 okręgu, który zawiera
okręgu, który zawiera 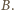 Wobec tego
Wobec tego 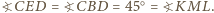 Na mocy
Na mocy 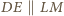 wynika stąd, iż
wynika stąd, iż 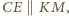 czyli
czyli 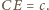 Zatem proste
Zatem proste 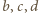 przecinają się w jednym punkcie
przecinają się w jednym punkcie 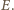
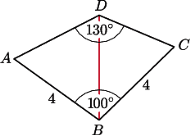
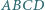 jest czworokątem wypukłym, w którym
jest czworokątem wypukłym, w którym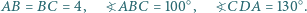
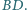
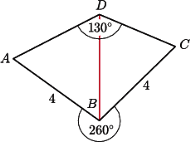
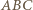 ma miarę
ma miarę 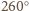 - dwa razy większą od kąta
- dwa razy większą od kąta 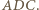 Zatem punkt
Zatem punkt 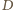 leży na okręgu o środku
leży na okręgu o środku 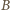 i promieniu
i promieniu 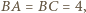 skąd
skąd 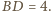
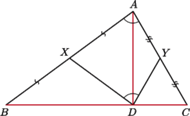
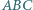 zachodzi
zachodzi 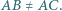 Punkty
Punkty 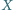 i
i 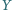 są odpowiednio środkami boków
są odpowiednio środkami boków 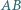 i
i 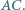 Na boku
Na boku 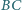 dany jest taki punkt
dany jest taki punkt 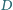 różny od środka boku, że
różny od środka boku, że 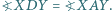 Wykazać, że
Wykazać, że 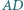 i
i 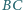 są prostopadłe.
są prostopadłe.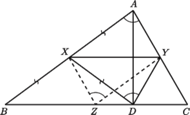
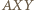 i
i 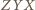 są przystające, to
są przystające, to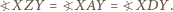
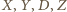 leżą na jednym okręgu. Stąd trapez
leżą na jednym okręgu. Stąd trapez 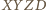 jest równoramienny, w szczególności
jest równoramienny, w szczególności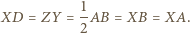
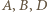 leżą więc na okręgu o środku
leżą więc na okręgu o środku 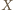 i promieniu
i promieniu 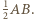 Innymi słowy, punkt
Innymi słowy, punkt 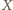 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 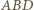 i jednocześnie jest środkiem boku
i jednocześnie jest środkiem boku 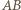 tego trójkąta. Ten trójkąt musi zatem mieć kąt prosty przy wierzchołku
tego trójkąta. Ten trójkąt musi zatem mieć kąt prosty przy wierzchołku 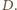
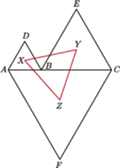
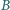 należy do odcinka
należy do odcinka 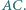 Punkty
Punkty 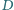 i
i 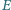 leżą po jednej stronie prostej
leżą po jednej stronie prostej 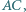 a punkt
a punkt 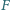 po drugiej, przy czym trójkąty
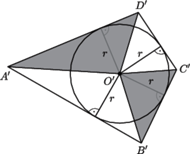
po drugiej, przy czym trójkąty 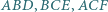 są równoboczne o ortocentrach odpowiednio
są równoboczne o ortocentrach odpowiednio 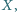
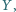
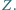 Udowodnić, że trójkąt
Udowodnić, że trójkąt 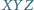 jest równoboczny.
jest równoboczny.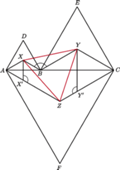
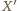 będzie takim punktem na odcinku
będzie takim punktem na odcinku 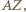 że
że 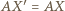 oraz niech
oraz niech 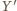 będzie takim punktem na odcinku
będzie takim punktem na odcinku 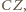 że
że 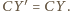
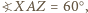 więc trójkąt
więc trójkąt 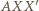 jest równoboczny. Podobnie trójkąt
jest równoboczny. Podobnie trójkąt 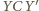 jest równoboczny. Zauważmy, że
jest równoboczny. Zauważmy, że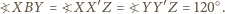
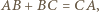 to
to 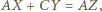 więc
więc 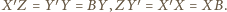 Zatem trójkąty
Zatem trójkąty 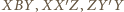 są przystające (cecha bkb). W szczególności
są przystające (cecha bkb). W szczególności 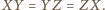
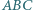 jest styczny do boków
jest styczny do boków 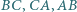 odpowiednio w punktach
odpowiednio w punktach 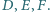 Udowodnij, że punkty
Udowodnij, że punkty 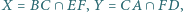
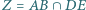 leżą na jednej prostej.
leżą na jednej prostej.
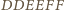 punkty
punkty 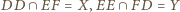 oraz
oraz 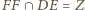 są współliniowe.
są współliniowe.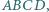 który nie jest trapezem, opisano okrąg. Wykaż, że punkty
który nie jest trapezem, opisano okrąg. Wykaż, że punkty 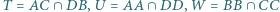 leżą na jednej prostej.
leżą na jednej prostej.
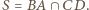 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 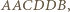 punkt
punkt 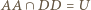 leży na prostej wyznaczonej przez punkty
leży na prostej wyznaczonej przez punkty 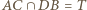 oraz
oraz 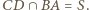 Z kolei z Twierdzenia Pascala dla
Z kolei z Twierdzenia Pascala dla 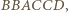 punkt
punkt 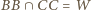 także leży na prostej wyznaczonej przez punkty
także leży na prostej wyznaczonej przez punkty 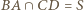 oraz
oraz 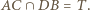
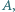
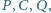
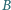 leżą w tej kolejności na łuku okręgu
leżą w tej kolejności na łuku okręgu 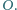 Na odcinkach
Na odcinkach 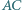 i
i 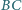 wybrano takie punkty odpowiednio
wybrano takie punkty odpowiednio 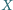 i
i 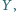 że
że 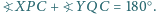 Wykaż, że wszystkie otrzymane w ten sposób proste
Wykaż, że wszystkie otrzymane w ten sposób proste 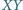 (przy ustalonych punktach
(przy ustalonych punktach 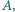
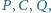
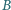 ) mają punkt wspólny.
) mają punkt wspólny.
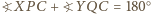 wynika, że punkt
wynika, że punkt 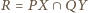 leży na okręgu
leży na okręgu 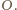 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 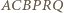 uzyskujemy współliniowość punktów
uzyskujemy współliniowość punktów 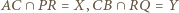 oraz niezależnego od
oraz niezależnego od 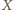 i
i 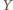 punktu
punktu 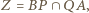 co kończy dowód.
co kończy dowód.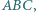 w którym
w którym 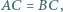 i takie punkty
i takie punkty 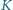 i
i 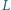 w jego wnętrzu, że
w jego wnętrzu, że 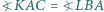 oraz
oraz 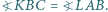 Udowodnij, że punkty
Udowodnij, że punkty 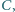
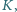
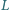 są współliniowe.
są współliniowe.
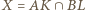 oraz
oraz 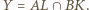 Z równoramienności trójkąta
Z równoramienności trójkąta 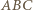 oraz danych równości kątów wynika, że
oraz danych równości kątów wynika, że 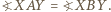 Ponieważ oba punkty
Ponieważ oba punkty 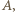
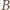 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 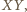 oznacza to, że punkty
oznacza to, że punkty 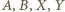 leżą na jednym okręgu.
leżą na jednym okręgu.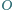 jest styczny do okręgu
jest styczny do okręgu 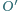 opisanego na trójkącie
opisanego na trójkącie 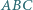 w punkcie
w punkcie 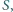 a do boków
a do boków 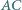 i
i 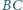 odpowiednio w punktach
odpowiednio w punktach 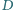 i
i 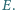 Wykaż, że środek okręgu wpisanego w trójkąt
Wykaż, że środek okręgu wpisanego w trójkąt 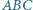 jest środkiem odcinka
jest środkiem odcinka 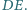
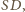
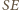 przecinają okrąg
przecinają okrąg 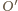 odpowiednio w drugich punktach
odpowiednio w drugich punktach 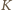 i
i 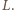 Warto rozważyć Twierdzenia Pascala dla sześciokąta
Warto rozważyć Twierdzenia Pascala dla sześciokąta 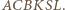
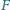 leży na boku
leży na boku 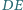 pięciokąta wypukłego
pięciokąta wypukłego 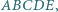 przy czym
przy czym 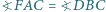 oraz
oraz 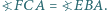 Wykaż, że
Wykaż, że 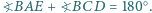
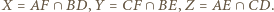
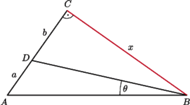
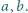 Rozważmy trójkąty prostokątne
Rozważmy trójkąty prostokątne
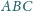 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
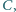 dla których
dla których
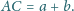 Niech
Niech
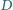 będzie punktem na
będzie punktem na
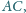 dla którego
dla którego
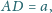
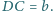 Znaleźć długość boku
Znaleźć długość boku
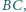 dla
której kąt
dla
której kąt
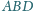 jest maksymalny.
jest maksymalny.
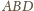 na dwa sposoby, mamy
na dwa sposoby, mamy
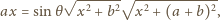
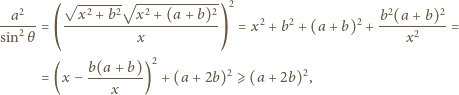
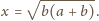 Kąt
Kąt
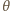 jest ostry, więc ma maksymalną wartość,
gdy
jest ostry, więc ma maksymalną wartość,
gdy
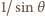 ma minimalną wartość, którą wyznaczyliśmy powyżej.
Zatem kąt
ma minimalną wartość, którą wyznaczyliśmy powyżej.
Zatem kąt
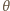 jest maksymalny dla
jest maksymalny dla
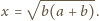
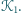 Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
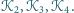 Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
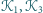 oraz
oraz
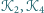 są prostopadłe.
są prostopadłe.
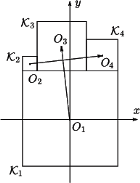
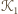 ma długość
ma długość
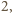 a kwadratów
a kwadratów
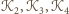 – odpowiednio
– odpowiednio
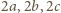 (stąd
(stąd
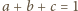 ).
Niech środek układu współrzędnych będzie ustawiony w środku
kwadratu
).
Niech środek układu współrzędnych będzie ustawiony w środku
kwadratu
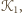 a osie niech będą równoległe do jego boków (jak na
rysunku). Oznaczmy środek kwadratu
a osie niech będą równoległe do jego boków (jak na
rysunku). Oznaczmy środek kwadratu
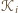 przez
przez
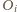 dla
dla
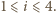
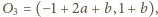 więc
więc
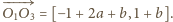 Podobnie,
skoro
Podobnie,
skoro
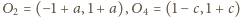 oraz
oraz
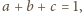 to otrzymujemy
to otrzymujemy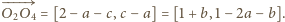 Stąd w oczywisty sposób
dostajemy
Stąd w oczywisty sposób
dostajemy
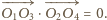
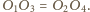
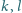 są styczne do okręgu
są styczne do okręgu
 w punktach
w punktach
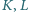 i przecinają
się w punkcie
i przecinają
się w punkcie
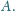 Punkt
Punkt
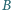 jest środkiem odcinka
jest środkiem odcinka
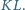 Wykazać, że punkty
Wykazać, że punkty
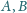 są symetryczne względem okręgu
są symetryczne względem okręgu
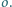
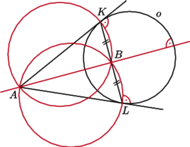
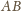 jest prostopadła do
jest prostopadła do
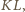 to jako bloki z definicji
można przyjąć okręgi o średnicach
to jako bloki z definicji
można przyjąć okręgi o średnicach
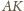 i
i
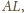 gdyż są
prostopadłe do
gdyż są
prostopadłe do
 i przechodzą przez
i przechodzą przez
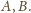 Oczywiście, sama
prosta
Oczywiście, sama
prosta
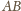 też się do tego celu nadaje.
też się do tego celu nadaje.
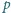 i
i
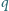 przecinają się w punktach
przecinają się w punktach
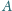 i
i
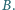 Prosta
Prosta
 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
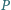 i
i
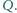 Punkt
Punkt
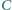 jest środkiem odcinka
jest środkiem odcinka
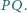 Wykazać,
że punkty
Wykazać,
że punkty
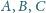 są współliniowe.
są współliniowe.

 będzie okręgiem o średnicy
będzie okręgiem o średnicy
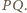 Okręgi
Okręgi
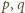 są
do niego prostopadłe, a zatem punkty
są
do niego prostopadłe, a zatem punkty
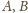 są symetryczne względem
są symetryczne względem
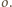 Stąd już wynika, że są współliniowe z punktem
Stąd już wynika, że są współliniowe z punktem
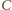 jako
środkiem tego okręgu – prosta poprowadzona z
jako
środkiem tego okręgu – prosta poprowadzona z
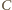 do punktu
do punktu
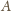 jest prostopadła do
jest prostopadła do
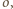 więc musi przechodzić przez punkt
więc musi przechodzić przez punkt
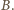
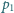 i
i
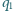 przecinają się w punktach
przecinają się w punktach
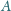 i
i
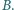 Prosta
Prosta
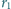 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
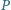 i
i
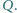 Punkt
Punkt
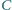 jest symetryczny do punktu
jest symetryczny do punktu
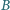 względem prostej
względem prostej
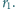 Okrąg
Okrąg
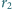 jest opisany na trójkącie
jest opisany na trójkącie
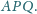 Proste
Proste
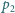 i
i
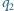 styczne do
styczne do
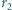 w punktach
odpowiednio
w punktach
odpowiednio
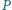 i
i
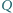 przecinają się w punkcie
przecinają się w punkcie
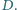 Wykazać,
że punkty
Wykazać,
że punkty
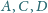 są współliniowe.
są współliniowe.
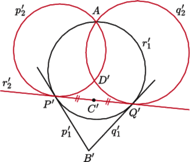
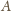 ; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
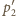 i
i
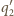 przecinają się w punktach
przecinają się w punktach
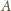 i
i
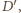 prosta
prosta
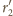 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach
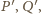 okrąg
okrąg
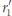 jest opisany na trójkącie
jest opisany na trójkącie
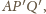 proste
proste
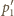 i
i
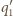 są styczne do
są styczne do
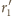 w punktach
w punktach
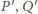 oraz
przecinają się w punkcie
oraz
przecinają się w punkcie
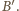
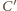 jest symetryczny do punktu
jest symetryczny do punktu
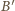 względem okręgu
względem okręgu
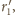 co na mocy zadania 1 oznacza, że jest
środkiem odcinka
co na mocy zadania 1 oznacza, że jest
środkiem odcinka
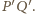 W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
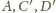 są współliniowe. Obrazem prostej
są współliniowe. Obrazem prostej
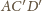 jest prosta
jest prosta
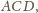 co kończy rozwiązanie.
co kończy rozwiązanie.
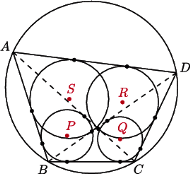
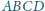 jest wpisany w okrąg. W trójkąty
jest wpisany w okrąg. W trójkąty
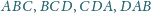 wpisano okręgi. Wykazać, że środki
wpisano okręgi. Wykazać, że środki
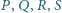 tych okręgów są wierzchołkami prostokąta.
tych okręgów są wierzchołkami prostokąta.