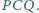Seminaria „Poznajemy OMG”»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Seminaria „Poznajemy OMG”
- Publikacja w Delcie: listopad 2012
- Publikacja elektroniczna: 01-11-2012
W czworokącie
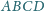 kąt
kąt
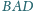 jest prosty. Wykaż, że
jest prosty. Wykaż, że

W czworokącie
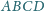 kąt
kąt
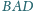 jest prosty. Wykaż, że
jest prosty. Wykaż, że

Znaleźć wszystkie trójkąty ostrokątne
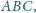 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
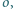 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
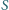 trójkąta
trójkąta
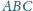 pokrywa się z ortocentrum
pokrywa się z ortocentrum
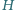 trójkąta
trójkąta
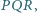 gdzie
gdzie
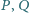 i
i
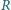 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
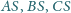 z okręgiem
z okręgiem
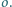
Udowodnij, że wśród dowolnych
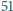 wierzchołków
wierzchołków
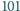 -kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
-kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.

Dany jest nierównoramienny trójkąt prostokątny
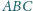 o kącie
prostym przy wierzchołku
o kącie
prostym przy wierzchołku
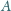 . Niech
. Niech
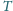 będzie środkiem
okręgu wpisanego, zaś
będzie środkiem
okręgu wpisanego, zaś
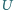 i
i
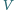 niech będą jego punktami
styczności odpowiednio z bokami
niech będą jego punktami
styczności odpowiednio z bokami
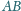 i
i
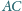 . Prosta
. Prosta
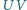 przecina w punkcie
przecina w punkcie
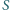 styczną do okręgu opisanego poprowadzoną
w punkcie
styczną do okręgu opisanego poprowadzoną
w punkcie
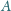 . Udowodnić, że proste
. Udowodnić, że proste
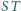 i
i
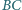 są równoległe.
są równoległe.
Udowodnij, że suma
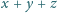 nie zależy od położenia punktu
nie zależy od położenia punktu
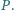
Punkt
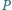 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
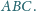 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
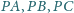 można zbudować
trójkąt.
można zbudować
trójkąt.
Wyznacz miary kątów trójkąta o bokach
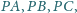 jeśli
jeśli
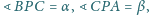
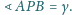
Punkt
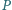 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
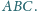 Wyznacz
pole trójkąta
Wyznacz
pole trójkąta
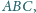 jeśli
jeśli
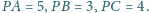
Punkt
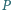 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
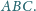 Udowodnij, że
Udowodnij, że
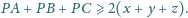
Na płaszczyźnie dane są punkty
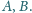 Rozważamy wszystkie
czworokąty wypukłe
Rozważamy wszystkie
czworokąty wypukłe
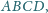 położone w ustalonej półpłaszczyźnie
o krawędzi
położone w ustalonej półpłaszczyźnie
o krawędzi
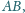 symetryczne względem prostej
symetryczne względem prostej
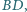 z kątem
prostym przy wierzchołku
z kątem
prostym przy wierzchołku
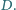 Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
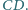
Podziel płaszczyznę na kwadraty, z których każde dwa są różnej wielkości.
Podziel kwadrat na mniejsze kwadraty, z których każde dwa są różnej wielkości.
Na ile różnych sposobów można ułożyć chodnik o długości
 i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
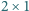 oraz
oraz
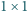 ?
?
W trójkącie
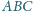 punkt
punkt
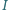 jest środkiem okręgu wpisanego.
Prosta
jest środkiem okręgu wpisanego.
Prosta
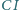 przecina bok
przecina bok
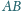 w punkcie
w punkcie
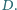 Prowadzimy
przez punkt
Prowadzimy
przez punkt
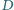 dowolną prostą, przecinającą okrąg opisany na
trójkącie
dowolną prostą, przecinającą okrąg opisany na
trójkącie
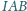 w punktach
w punktach
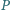 i
i
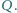 Wykazać, że prosta
Wykazać, że prosta
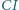 jest dwusieczną kąta
jest dwusieczną kąta