Potęga punktu względem okręgu»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Potęga punktu względem okręgu
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (417 KB)
Odcinek 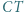 jest wysokością trójkąta
jest wysokością trójkąta 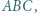 w którym
w którym 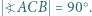 Okrąg o środku
Okrąg o środku 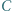 i promieniu
i promieniu 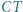 oraz okrąg opisany na trójkącie
oraz okrąg opisany na trójkącie 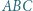 przecinają się w punktach
przecinają się w punktach 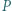 i
i 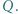 Dowieść, że prosta
Dowieść, że prosta 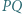 przechodzi przez środek odcinka
przechodzi przez środek odcinka 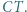
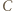 ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.
ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.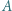 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 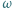 o środku
o środku 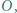 w punktach
w punktach 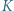 i
i 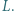 Punkt
Punkt 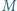 jest środkiem odcinka
jest środkiem odcinka 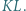 Okrąg
Okrąg 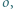 przechodzący przez punkty
przechodzący przez punkty 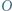 i
i 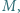 przecina okrąg
przecina okrąg 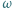 w punktach
w punktach 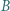 i
i 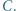 Wykazać, że punkty
Wykazać, że punkty 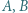 i
i 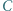 leżą na jednej prostej.
leżą na jednej prostej.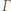 będzie okręgiem o średnicy
będzie okręgiem o średnicy 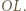 Wówczas okrąg
Wówczas okrąg 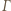 przechodzi przez punkt
przechodzi przez punkt 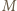 i jest styczny do prostej
i jest styczny do prostej 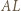 w punkcie
w punkcie 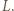 Wystarczy zauważyć, że punkt
Wystarczy zauważyć, że punkt 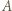 ma jednakową potęgę względem okręgów
ma jednakową potęgę względem okręgów 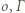 i
i 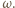
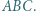 Okrąg styczny do odcinków
Okrąg styczny do odcinków 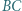 i
i 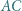 przecina odcinek
przecina odcinek 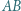 w punktach
w punktach 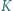 i
i 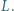 Wykazać, że
Wykazać, że 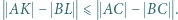
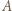 i
i 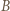 względem okręgu z zadania i odjąć stronami otrzymane równości.
względem okręgu z zadania i odjąć stronami otrzymane równości.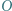 jest środkiem okręgu opisanego, a punkt
jest środkiem okręgu opisanego, a punkt 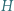 ortocentrum trójkąta ostrokątnego i różnobocznego
ortocentrum trójkąta ostrokątnego i różnobocznego 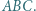 Punkty
Punkty 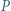 i
i 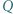 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 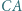 i
i 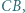 przy czym czworokąt
przy czym czworokąt 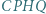 jest równoległobokiem. Wykazać, że
jest równoległobokiem. Wykazać, że 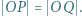
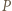 i
i 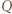 mają równą potęgę względem okręgu opisanego na trójkącie
mają równą potęgę względem okręgu opisanego na trójkącie 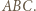 Do tego celu wystarczy podobieństwo odpowiednich trójkątów.
Do tego celu wystarczy podobieństwo odpowiednich trójkątów.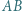 i prostopadła do niej cięciwa
i prostopadła do niej cięciwa 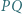 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 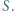 Okrąg
Okrąg 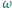 jest styczny (wewnętrznie) do okręgu
jest styczny (wewnętrznie) do okręgu  i do odcinków
i do odcinków 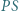 oraz
oraz 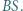 Niech
Niech 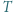 będzie punktem styczności okręgu
będzie punktem styczności okręgu 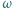 do odcinka
do odcinka 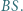 Wykazać, że
Wykazać, że 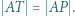
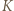 i
i 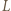 będą punktami styczności okręgu
będą punktami styczności okręgu 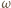 do, odpowiednio, okręgu
do, odpowiednio, okręgu  i odcinka
i odcinka 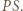 Wówczas punkty
Wówczas punkty 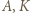 i
i 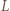 są współliniowe, gdyż punkt
są współliniowe, gdyż punkt 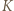 jest obrazem punktu
jest obrazem punktu 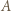 w jednokładności względem punktu
w jednokładności względem punktu 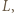 która przekształca okrąg
która przekształca okrąg  na
na 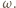 Mamy też
Mamy też 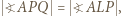 bo są to kąty wpisane, oparte na równej długości łukach okręgu
bo są to kąty wpisane, oparte na równej długości łukach okręgu  Resztę załatwia podobieństwo trójkątów i potęga punktu
Resztę załatwia podobieństwo trójkątów i potęga punktu 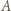 względem okręgu
względem okręgu 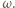
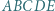 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 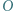 ; przy tym
; przy tym 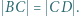 Przekątne
Przekątne 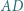 i
i 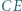 są prostopadłe, zaś przekątne
są prostopadłe, zaś przekątne 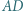 i
i 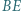 przecinają się w takim punkcie
przecinają się w takim punkcie 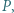 że
że 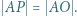 Wykazać, że trójkąt
Wykazać, że trójkąt 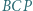 jest równoboczny.
jest równoboczny.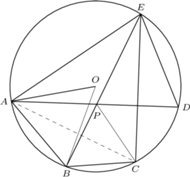
 punkt
punkt  jest środkiem łuku
jest środkiem łuku 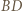 ; zatem prosta
; zatem prosta 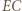 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 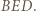 Przy tym jest prostopadła do prostej
Przy tym jest prostopadła do prostej 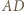 ; jest więc symetralną odcinka
; jest więc symetralną odcinka 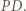 Stąd wynika, że
Stąd wynika, że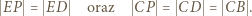
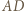 i
i 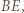 przecinające się w punkcie
przecinające się w punkcie 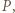 wyznaczają trójkąty podobne:
wyznaczają trójkąty podobne: 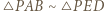 ; a ponieważ
; a ponieważ 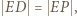 zatem
zatem 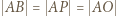 (ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 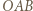 jest równoboczny, wobec czego
jest równoboczny, wobec czego 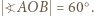 W takim razie
W takim razie 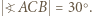
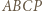 to deltoid
to deltoid 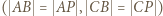 ; stąd
; stąd 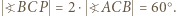 Wobec wcześniejszego spostrzeżenia, że
Wobec wcześniejszego spostrzeżenia, że 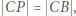 dostajemy tezę zadania: trójkąt
dostajemy tezę zadania: trójkąt 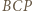 jest równoboczny.
jest równoboczny.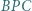 i
i 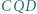 są równoboczne i leżą na zewnątrz równoległoboku
są równoboczne i leżą na zewnątrz równoległoboku 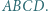 Udowodnić, że trójkąt
Udowodnić, że trójkąt 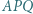 też jest równoboczny.
też jest równoboczny.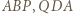 i
i 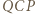 są przystające (bkb).
są przystające (bkb).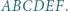 Punkty
Punkty 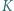 i
i 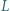 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 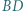 i
i 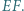 Dowieść, że trójkąt
Dowieść, że trójkąt 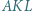 jest równoboczny.
jest równoboczny.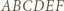 na
na 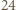 przystające trójkąty równoboczne można zauważyć, że odcinki
przystające trójkąty równoboczne można zauważyć, że odcinki 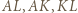 są dłuższymi przekątnymi przystających równoległoboków
są dłuższymi przekątnymi przystających równoległoboków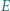 i
i 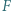 leżą odpowiednio na bokach
leżą odpowiednio na bokach 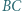 i
i 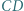 prostokąta
prostokąta 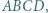 przy czym trójkąt
przy czym trójkąt 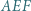 jest równoboczny. Punkt
jest równoboczny. Punkt 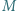 jest środkiem odcinka
jest środkiem odcinka 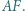 Wykazać, że trójkąt
Wykazać, że trójkąt 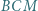 jest równoboczny.
jest równoboczny.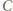 i
i 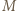 leżą na okręgu o średnicy
leżą na okręgu o średnicy 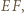 więc
więc 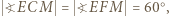 analogicznie
analogicznie 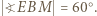
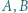 i
i 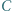 leżą kolejno na prostej
leżą kolejno na prostej 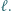 Punkty
Punkty 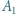 i
i 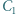 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 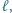 przy czym trójkąty
przy czym trójkąty 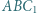 i
i 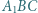 są równoboczne. Punkty
są równoboczne. Punkty 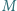 i
i 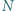 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 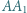 i
i 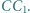 Udowodnić, że trójkąt
Udowodnić, że trójkąt 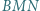 jest równoboczny.
jest równoboczny.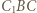 wokół punktu
wokół punktu 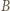 o
o 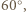 otrzymamy trójkąt
otrzymamy trójkąt 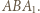 Obrazem punktu
Obrazem punktu 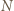 w tym obrocie jest punkt
w tym obrocie jest punkt 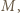 więc
więc 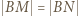 i
i 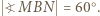
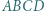 i punkt
i punkt 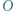 wewnątrz niego, przy czym zachodzą równości:
wewnątrz niego, przy czym zachodzą równości: 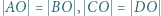 i
i 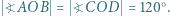 Dowieść, że środki odcinków
Dowieść, że środki odcinków 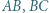 i
i 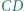 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.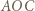 o
o 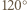 wokół punktu
wokół punktu 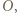 otrzymamy trójkąt
otrzymamy trójkąt 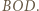 Zatem te trójkąty są przystające oraz proste
Zatem te trójkąty są przystające oraz proste 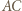 i
i 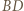 przecinają się pod kątem
przecinają się pod kątem 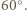
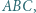 na zewnątrz niego, zbudowano trójkąty równoboczne
na zewnątrz niego, zbudowano trójkąty równoboczne 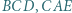 i
i 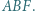 Środkami tych trójkątów są odpowiednio punkty
Środkami tych trójkątów są odpowiednio punkty 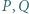 i
i 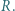 Dowieść, że trójkąt
Dowieść, że trójkąt 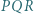 jest równoboczny (twierdzenie Napoleona).
jest równoboczny (twierdzenie Napoleona).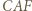 jest podobny do trójkąta
jest podobny do trójkąta 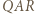 w skali
w skali 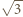 (bkb), analogicznie trójkąt
(bkb), analogicznie trójkąt 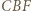 do
do 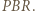 Stąd
Stąd 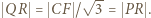 Tą samą metodą dowodzimy, że
Tą samą metodą dowodzimy, że 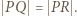
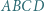 o podstawach
o podstawach 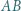 i
i 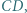 w którym
w którym 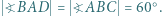 Na boku
Na boku 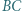 tego trapezu leży taki punkt
tego trapezu leży taki punkt 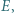 że
że 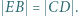 Wykazać, że
Wykazać, że 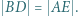
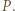 Wówczas trójkąty
Wówczas trójkąty 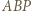 i
i 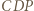 są równoboczne, dalej dowodzimy, że trójkąty
są równoboczne, dalej dowodzimy, że trójkąty 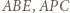 i
i 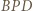 są przystające (bkb).
są przystające (bkb).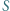 leży wewnątrz sześciokąta foremnego
leży wewnątrz sześciokąta foremnego 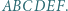 Udowodnić, że suma pól trójkątów
Udowodnić, że suma pól trójkątów 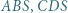 i
i 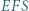 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 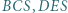 i
i 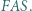
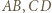 i
i 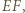 otrzymując trójkąt równoboczny. Suma pól trójkątów
otrzymując trójkąt równoboczny. Suma pól trójkątów 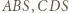 i
i 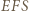 stanowi
stanowi 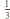 pola tego trójkąta.
pola tego trójkąta.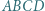 mamy
mamy 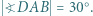 Wykazać, że
Wykazać, że 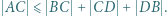
 będzie punktem symetrycznym do
będzie punktem symetrycznym do 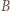 względem prostej
względem prostej 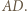 Wówczas trójkąt
Wówczas trójkąt 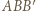 jest równoboczny oraz
jest równoboczny oraz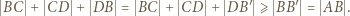
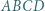 wszystkie kąty płaskie przy wierzchołku
wszystkie kąty płaskie przy wierzchołku 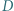 mają miarę
mają miarę 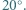 Wykazać, że
Wykazać, że 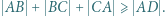
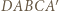 będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi
będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi 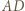 i usunięciu ściany
i usunięciu ściany 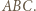 Wówczas trójkąt
Wówczas trójkąt 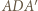 jest równoboczny.
jest równoboczny.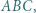 w którym
w którym 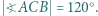 Punkt
Punkt 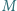 jest środkiem boku
jest środkiem boku 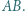 Na odcinkach
Na odcinkach 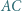 i
i 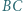 wybrano odpowiednio takie punkty
wybrano odpowiednio takie punkty 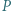 i
i 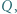 że
że 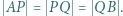 Wykazać, że
Wykazać, że 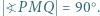
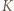 będzie symetryczny do
będzie symetryczny do 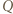 względem
względem 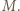 Wówczas trójkąt
Wówczas trójkąt 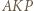 jest równoboczny.
jest równoboczny.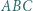 mamy
mamy 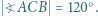 Punkty
Punkty 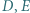 i
i 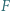 leżą na bokach odpowiednio
leżą na bokach odpowiednio 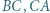 i
i 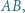 przy czym proste
przy czym proste 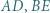 i
i 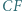 są dwusiecznymi kątów trójkąta
są dwusiecznymi kątów trójkąta 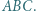 Udowodnić, że
Udowodnić, że 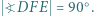
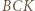 na zewnątrz trójkąta
na zewnątrz trójkąta 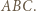 Wtedy
Wtedy 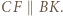 Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów
Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów 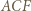 i
i 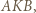 wykażemy, że
wykażemy, że 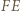 jest dwusieczną kąta
jest dwusieczną kąta 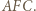 Analogicznie
Analogicznie 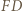 jest dwusieczną kąta
jest dwusieczną kąta 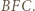
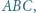 w którym
w którym 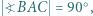 jest podstawą ostrosłupa
jest podstawą ostrosłupa 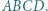 Ponadto zachodzą równości
Ponadto zachodzą równości 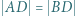 oraz
oraz 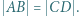 Udowodnić, że
Udowodnić, że 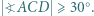
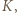 by czworokąt
by czworokąt 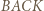 był prostokątem. Wtedy trójkąt
był prostokątem. Wtedy trójkąt 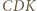 jest równoboczny. Z nierówności kąta trójściennego mamy
jest równoboczny. Z nierówności kąta trójściennego mamy 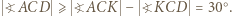
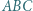 wybrano taki punkt
wybrano taki punkt 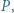 dla którego wartość wyrażenia
dla którego wartość wyrażenia 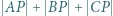 jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że
jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że 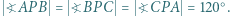
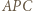 o
o 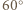 wokół punktu
wokół punktu 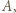 w kierunku zgodnym z orientacją trójkąta
w kierunku zgodnym z orientacją trójkąta 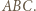 Otrzymamy trójkąt
Otrzymamy trójkąt 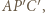 przystający do
przystający do 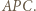 Trójkąt
Trójkąt 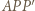 jest równoboczny, więc
jest równoboczny, więc 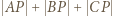 jest równe długości łamanej
jest równe długości łamanej 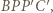 która jest najkrótsza, gdy jej wierzchołki są współliniowe.
która jest najkrótsza, gdy jej wierzchołki są współliniowe.