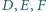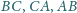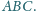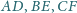Warto dobrze ustawić»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Warto dobrze ustawić
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
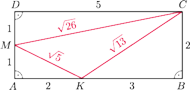
Oblicz pole trójkąta o bokach długości
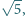
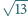 i
i
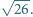
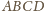 o bokach
o bokach
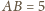 i
i
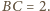 Niech
punkt
Niech
punkt
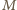 będzie środkiem boku
będzie środkiem boku
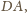 a punkt
a punkt
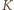 niech należy
do boku
niech należy
do boku
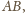 przy czym
przy czym
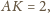
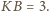 Wtedy z twierdzenia
Pitagorasa
Wtedy z twierdzenia
Pitagorasa
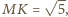
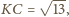
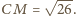 Należy
obliczyć pole trójkąta
Należy
obliczyć pole trójkąta
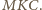 Jest ono równe
Jest ono równe
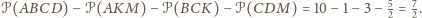
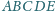 kąty przy wierzchołkach
kąty przy wierzchołkach
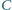 i
i
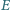 są proste. Oblicz
są proste. Oblicz
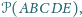 jeśli
jeśli
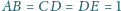 oraz
oraz
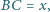
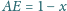 dla
dla
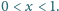
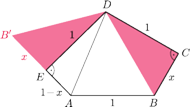
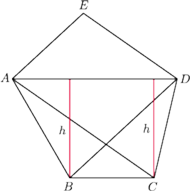
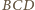 obok trójkąta
obok trójkąta
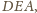 jak na rysunku
(
jak na rysunku
(
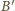 oznacza odpowiednik wierzchołka
oznacza odpowiednik wierzchołka
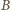 ). Wtedy w trójkącie
). Wtedy w trójkącie
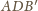 podstawa
podstawa
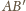 ma długość
ma długość
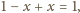 wysokość
wysokość
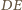 jest równa 1, więc pole jest równe
jest równa 1, więc pole jest równe
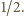 Pozostałą
częścią pięciokąta jest trójkąt
Pozostałą
częścią pięciokąta jest trójkąt
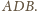 Przystaje on do trójkąta
Przystaje on do trójkąta
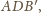 ponieważ
ponieważ
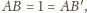
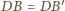 oraz bok
oraz bok
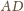 jest wspólny. Stąd
jest wspólny. Stąd
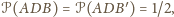 więc pole
pięciokąta równe jest 1.
więc pole
pięciokąta równe jest 1.
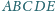 , w którym pola trójkątów
, w którym pola trójkątów
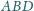 ,
,
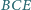 ,
,
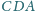 ,
,
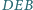 i
i
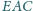 są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
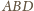 i
i
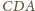 mają równe pola oraz wspólny
bok
mają równe pola oraz wspólny
bok
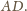 Wobec tego wysokości tych trójkątów poprowadzone do
boku
Wobec tego wysokości tych trójkątów poprowadzone do
boku
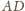 są równe. Ponadto punkty
są równe. Ponadto punkty
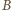 i
i
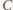 leżą po
tej samej stronie prostej
leżą po
tej samej stronie prostej
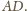 Stąd wniosek, że przekątna
Stąd wniosek, że przekątna
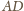 jest
równoległa do boku
jest
równoległa do boku
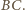 Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
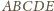 są równoległe do odpowiednich jego
boków
są równoległe do odpowiednich jego
boków
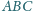 o kącie prostym
przy wierzchołku
o kącie prostym
przy wierzchołku
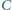 . Znaleźć zbiór takich punktów
. Znaleźć zbiór takich punktów
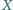 z wnętrza trójkąta
z wnętrza trójkąta
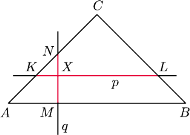
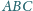 , że jeśli prosta
, że jeśli prosta
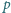 równoległa do
podstawy
równoległa do
podstawy
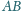 przechodząca przez punkt
przechodząca przez punkt
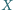 przecina ramiona
przecina ramiona
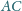 i
i
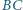 w punktach
w punktach
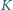 i
i
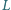 , zaś
, zaś
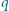 jest prostą
prostopadłą do
jest prostą
prostopadłą do
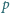 przechodzącą przez
przechodzącą przez
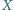 , przecinającą podstawę
, przecinającą podstawę
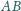 trójkąta w punkcie
trójkąta w punkcie
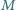 , a ramię w punkcie
, a ramię w punkcie
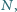 to
to
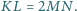
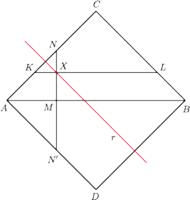
 przecina ramię
przecina ramię
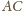 . Rozszerzmy nasz
trójkąt do kwadratu
. Rozszerzmy nasz
trójkąt do kwadratu
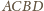 .
.
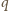 z nowo dorysowanym bokiem kwadratu
oznaczmy przez
z nowo dorysowanym bokiem kwadratu
oznaczmy przez
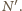 Szukamy takich punktów
Szukamy takich punktów
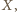 że
że
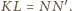 Równoważnie takich, że odcinki
Równoważnie takich, że odcinki
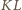 i
i
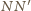 są symetryczne względem prostej
są symetryczne względem prostej
 prostopadłej do
prostopadłej do
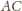 przechodzącej przez
przechodzącej przez
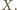 To zachodzi wtedy i tylko wtedy, gdy
trójkąty
To zachodzi wtedy i tylko wtedy, gdy
trójkąty
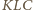 i
i
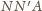 są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
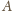 i
i
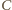 są symetryczne
względem
są symetryczne
względem
 (bo punkty
(bo punkty
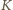 i
i
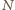 zostały skonstruowane tak,
że są symetryczne względem
zostały skonstruowane tak,
że są symetryczne względem
 ).
).
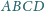 i
i
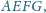 tak samo zorientowane, mają wspólny
tylko punkt
tak samo zorientowane, mają wspólny
tylko punkt
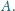 Wykaż, że
Wykaż, że
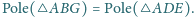
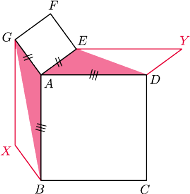
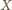 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
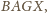 a
a
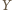 – czwartym wierzchołkiem równoległoboku
– czwartym wierzchołkiem równoległoboku
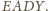 Równoległoboki te są przystające, ponieważ
Równoległoboki te są przystające, ponieważ
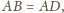
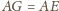 oraz
oraz
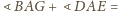
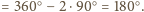 Stąd
Stąd
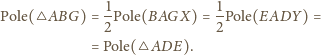
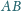 i
i
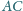 trójkąta
trójkąta
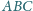 zbudowano, po jego
zewnętrznej stronie, kwadraty
zbudowano, po jego
zewnętrznej stronie, kwadraty
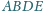 i
i
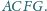 Punkty
Punkty
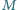 i
i
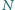 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
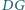 i
i
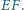 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia
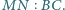
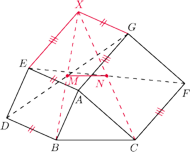
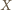 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
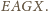 Wtedy
Wtedy
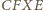 także jest równoległobokiem (bo
także jest równoległobokiem (bo
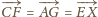 ). Wobec tego punkt
). Wobec tego punkt
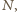 jako środek jego przekątnej
jako środek jego przekątnej
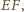 jest też środkiem drugiej przekątnej
jest też środkiem drugiej przekątnej
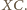 Analogicznie
Analogicznie
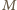 jest środkiem
jest środkiem
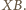 Stąd i z twierdzenia Talesa uzyskujemy
Stąd i z twierdzenia Talesa uzyskujemy
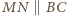 oraz
oraz
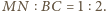
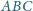 zachodzi równość
zachodzi równość
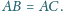 Punkt
Punkt
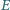 jest środkiem wysokości
jest środkiem wysokości
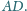 Punkt
Punkt
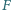 jest rzutem
prostokątnym punktu
jest rzutem
prostokątnym punktu
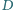 na prostą
na prostą
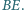 Udowodnij, że
Udowodnij, że
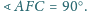
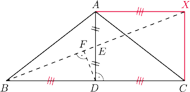
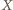 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
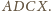 Wtedy
Wtedy
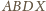 jest równoległobokiem o środku
jest równoległobokiem o środku
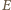 (bo
(bo
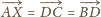 oraz
oraz
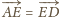 ), więc punkty
), więc punkty
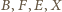 są
współliniowe. Odcinki
są
współliniowe. Odcinki
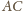 i
i
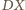 są średnicami okręgu opisanego
na prostokącie
są średnicami okręgu opisanego
na prostokącie
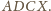 Ponadto
Ponadto
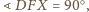 więc punkt
więc punkt
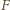 leży na tym okręgu. Stąd
leży na tym okręgu. Stąd
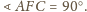
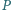 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
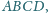 przy czym
przy czym
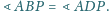 Wykaż, że
Wykaż, że
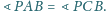
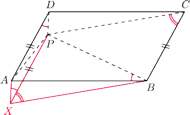
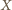 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
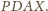 Wtedy
Wtedy
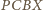 także jest równoległobokiem oraz
zachodzą równości
także jest równoległobokiem oraz
zachodzą równości
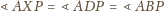
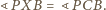
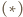 (uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
(uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
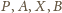 leżą na jednym okręgu. Wobec
tego
leżą na jednym okręgu. Wobec
tego
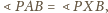 co razem z równością
co razem z równością
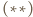 daje tezę.
daje tezę.
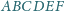 o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
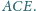
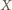 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
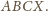 Wtedy
Wtedy
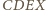 i
i
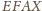 też są równoległobokami...
też są równoległobokami...
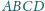 punkty
punkty
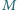 i
i
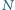 są środkami odpowiednio
ramion
są środkami odpowiednio
ramion
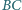 i
i
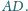 Wykaż, że
Wykaż, że
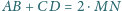 i że
i że


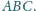 Wykaż, że z jego środkowych można
zbudować trójkąt.
Wykaż, że z jego środkowych można
zbudować trójkąt.
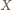 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
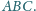 Punkty
Punkty
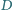 i
i
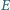 należą odpowiednio do boków
należą odpowiednio do boków
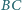 i
i
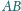 tego
trójkąta i
tego
trójkąta i
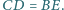 Punkt
Punkt
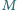 jest środkiem odcinka
jest środkiem odcinka
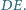 Udowodnij, że
Udowodnij, że
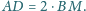
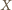 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
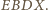
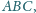 w którym
w którym
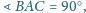 jest podstawą
ostrosłupa
jest podstawą
ostrosłupa
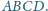 Ponadto zachodzą równości
Ponadto zachodzą równości
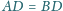 oraz
oraz
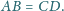 Wykaż, że
Wykaż, że
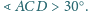
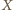 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
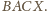
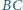 trójkąta
trójkąta
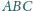 wybrano punkt
wybrano punkt
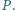 Punkty
Punkty
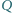 i
i
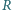 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
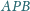 i
i
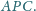 Punkt
Punkt
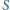 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
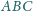 do boku
do boku
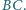 Wykazać, że punkty
Wykazać, że punkty
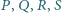 leżą na
jednym okręgu.
leżą na
jednym okręgu.
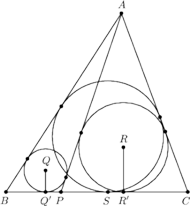
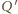 i
i
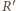 oznaczają rzuty punktów
oznaczają rzuty punktów
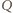 i
i
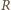 na
prostą
na
prostą
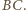 Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
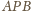 wynika równość
wynika równość
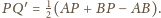 Podobnie mamy
Podobnie mamy
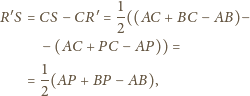
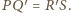 Stąd również
Stąd również
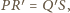 czyli
czyli
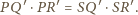
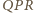 między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
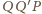 i
i
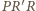 są podobne. W takim
razie
są podobne. W takim
razie
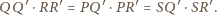
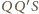 i
i
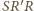 są podobne, więc kąt
są podobne, więc kąt
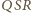 też
jest prosty. To oznacza, że punkty
też
jest prosty. To oznacza, że punkty
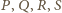 leżą na jednym
okręgu.
leżą na jednym
okręgu.
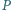 leżącego
wewnątrz trójkąta równobocznego
leżącego
wewnątrz trójkąta równobocznego
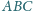 o boku
o boku
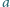 od jego
wierzchołków jest nie większa niż
od jego
wierzchołków jest nie większa niż
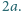
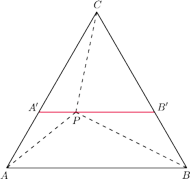
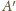 i
i
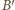 będą punktami przecięcia prostej równoległej
do
będą punktami przecięcia prostej równoległej
do
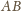 i przechodzącej przez punkt
i przechodzącej przez punkt
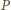 odpowiednio z bokami
odpowiednio z bokami
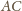 i
i
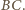 Trójkąt
Trójkąt
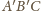 jest równoboczny i
jest równoboczny i
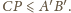 Ponadto stosując nierówność trójkąta, dostaniemy
Ponadto stosując nierówność trójkąta, dostaniemy
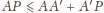 oraz
oraz
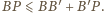 Dodając te trzy nierówności stronami,
otrzymujemy
Dodając te trzy nierówności stronami,
otrzymujemy
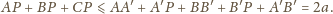
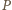 jest jednym z wierzchołków trójkąta
jest jednym z wierzchołków trójkąta
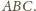
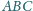 jest styczny do boków
jest styczny do boków
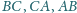 odpowiednio w punktach
odpowiednio w punktach
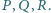 Odcinek
Odcinek
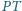 jest średnicą tego
okręgu. Proste
jest średnicą tego
okręgu. Proste
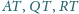 przecinają prostą
przecinają prostą
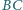 odpowiednio
w punktach
odpowiednio
w punktach
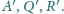 Wykazać, że
Wykazać, że
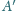 jest środkiem odcinka
jest środkiem odcinka
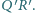
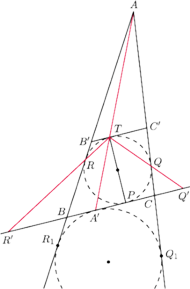
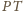 jest średnicą, to styczna do okręgu wpisanego w punkcie
jest średnicą, to styczna do okręgu wpisanego w punkcie
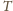 jest równoległa do
jest równoległa do
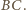 Niech
Niech
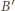 i
i
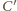 będą punktami
przecięcia tej stycznej z bokami
będą punktami
przecięcia tej stycznej z bokami
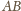 i
i
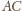 (
(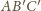 i
i
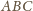 są jednokładne, skąd natychmiast wynika, że
punkt
są jednokładne, skąd natychmiast wynika, że
punkt
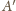 jest punktem styczności okręgu dopisanego z bokiem
jest punktem styczności okręgu dopisanego z bokiem
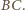 Z równoległości
Z równoległości
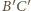 i
i
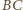 wynika też, że trójkąty
wynika też, że trójkąty
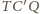 i
i
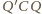 są podobne, a skoro
są podobne, a skoro
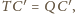 to
to
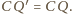 Niech
Niech
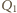 będzie punktem styczności okręgu
dopisanego, stycznego do
będzie punktem styczności okręgu
dopisanego, stycznego do
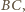 z prostą
z prostą
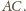 W takim razie
W takim razie
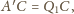 a stąd natychmiast wynika, że
a stąd natychmiast wynika, że
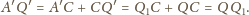
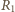 punkt styczności okręgu dopisanego
z bokiem
punkt styczności okręgu dopisanego
z bokiem
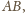 udowodnimy, że
udowodnimy, że
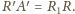 Ale
Ale
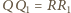 – dowód jest więc zakończony.
– dowód jest więc zakończony.
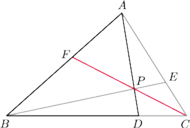
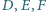 należą odpowiednio do boków
należą odpowiednio do boków
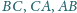 trójkąta
trójkąta
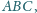 proste
proste
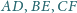 przecinają się w punkcie
przecinają się w punkcie
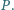 Wykaż, że
Wykaż, że

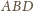 i prostej
i prostej
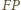 zachodzi
zachodzi
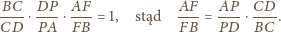
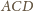 i prostej
i prostej
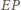 otrzymujemy
otrzymujemy

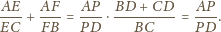
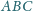 punkty
punkty
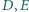 są spodkami dwusiecznych
odpowiednio
są spodkami dwusiecznych
odpowiednio
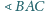 i
i
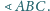 Punkt
Punkt
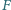 jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
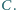 Udowodnij, że
punkty
Udowodnij, że
punkty
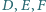 leżą na jednej prostej.
leżą na jednej prostej.
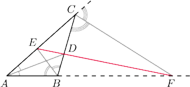
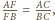
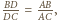
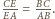 Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
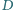 i
i
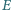 leżą odpowiednio na bokach
leżą odpowiednio na bokach
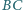 i
i
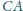 trójkąta
trójkąta
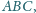 a punkt
a punkt
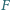 na przedłużeniu boku
na przedłużeniu boku
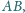 przy czym punkty
przy czym punkty
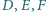 są współliniowe. Punkty
są współliniowe. Punkty
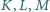 są odpowiednio środkami boków
są odpowiednio środkami boków
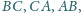 zaś punkty
zaś punkty
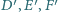 – obrazami symetrycznymi punktów
– obrazami symetrycznymi punktów
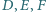 w symetriach względem
w symetriach względem
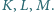 Wykaż, że punkty
Wykaż, że punkty
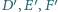 są
współliniowe.
są
współliniowe.