Ponieważ jednak z natury jesteśmy dociekliwi i nie lubimy brać czegoś na tak zwaną wiarę, przeprowadźmy małą symulację tego zjawiska. Będzie w pełni bezpieczna i można ją wykonać samodzielnie w domu. Weźmy dwie kartki papieru i suszarkę do włosów, a następnie skierujmy strumień powietrza pomiędzy kartki. (Przed przeprowadzeniem doświadczenia dobrze jest się z kimś założyć o to, co się stanie z kartkami!) Niemożliwe! Kartki zamiast polecieć w dwie różne strony przyciągnęły się! Teraz już widać, że podobnie może się stać z człowiekiem stojącym zbyt blisko nadjeżdżającego pociągu.

Skoro już wiemy, co się dzieje, spróbujmy, Drogi Czytelniku, wyjaśnić, dlaczego tak jest. Wyobraź sobie rurę, przez którą płynie woda i w pewnym momencie napotyka zwężenie (rysunek). Jak Ci się wydaje, czy woda będzie płynąć przez nie szybciej, czy wolniej? A co dzieje się z ciśnieniem w tym przewężeniu? W celu znalezienia odpowiedzi na to pytanie zastanówmy się, co w tym przypadku nie ulegnie zmianie. Na pewno pamiętasz wielkość, która w przyrodzie jest zachowana. Tak, chodzi o energię. To właśnie od zasady zachowania energii zaczniemy nasze rozważania dotyczące wody w rurze. Spójrz teraz na rysunek poniżej.

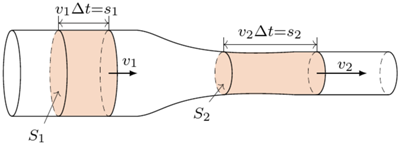
Widzimy na nim ciecz w rurze o zmiennym przekroju. Kolorem zaznaczona jest pewna ilość cieczy o tej samej masie, która jest iloczynem gęstości i objętości danego "fragmentu":

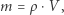gdzie 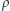jest gęstością cieczy, a 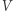jej objętością.

Woda płynąc, porusza się z jakąś prędkością, zatem ma energię kinetyczną, którą można wyrazić wzorem:

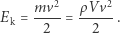Jeżeli nasza ciecz znajduje się na jakiejś wysokości, ma też energię potencjalną grawitacji:

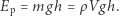Nie możemy też zapomnieć o ruchu cząsteczek wewnątrz cieczy. Im również odpowiada pewien rodzaj energii, który nazwiemy roboczo energią chaotyczną, ponieważ taki właśnie jest ruch tych cząsteczek. Poruszając się, cząsteczki wywierają ciśnienie na krawędzie naszego fragmentu cieczy. Działają więc pewną siłą 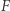na powierzchnię 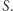Aby taki fragment okiełznać, a więc pozbawić go omawianej energii, należałoby go ścisnąć do nieskończenie małych rozmiarów, czyli przeciwdziałać sile 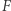na drodze 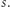Z tego wynika, że energię chaotyczną możemy zapisać wzorem:

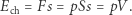Mamy już wszystkie energie i możemy je sprowadzić do jednej postaci, uwzględniając fakt, że musi ona pozostać stała:

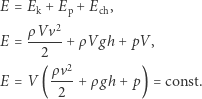Ponieważ objętość naszego fragmentu cieczy się nie zmienia, czynnik w nawiasie również musi pozostać stały. Mamy więc ostatecznie sformułowane prawo:

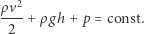Jest to prawo Bernoulliego, które jest spełnione nie tylko dla wody, ale również dla innych płynów, w tym omawianego na początku powietrza! (Tak, w języku fizyki płyn to nie tylko ciecz, ale również gaz.) Na mocy tego prawa możemy zauważyć, że przy zaniedbywalnie małej różnicy wysokości w momencie, w którym prędkość płynu rośnie, maleje jego ciśnienie. Możemy więc spokojnie wrócić do omawianego na początku przykładu z pociągiem i kartkami. Teraz jest już jasne, że w momencie, gdy pociąg wjeżdża na stację, powietrze, które znajduje się pomiędzy pociągiem a człowiekiem stojącym blisko niego, porusza się szybciej, a więc ma niższe ciśnienie. Wiesz też, że ruch powietrza odbywa się w kierunku od wysokiego do niskiego ciśnienia. Oczywiste zatem staje się, że obiekty znajdujące się w bliskiej odległości od pociągu będą pod niego wessane. Ciekawe, że prawo to na skutek błędnego wyobrażenia zostało również nazwane paradoksem hydrostatycznym. Faktycznie, jak sami się pewnie przekonaliście, rozumowanie to nie jest całkowicie intuicyjne. Jednak w życiu codziennym zjawisko to występuję częściej. Weźmy na przykład drzwi trzaskające podczas przeciągu, silne podmuchy wiatru między budynkami lub na schodach w podziemnym przejściu. Podobnie nurt w rzece - zawsze wciąga obiekty na środek, a najsilniejszy występuje między wysepkami. Zjawisko to może stwarzać niebezpieczeństwo w żegludze, gdy dwa statki płyną równolegle, woda między nimi płynie szybciej i statki mogą się zderzyć. Jak widać, zjawisk tych jest bardzo dużo i potrafimy je wyjaśnić w stosunkowo nieskomplikowany sposób. Ciebie, Drogi Czytelniku, zachęcam do obserwowania otaczającego Cię świata i znajdowania kolejnych przykładów.

A na koniec zagadka. Potrzebne jest pudełko, suszarka i zapalona świeca. Ustaw świecę za rogiem pudełka i skieruj strumień powietrza z suszarki wzdłuż niego. W którą stronę przesunie się płomień świecy? Zostanie wypchnięty czy wciągnięty przez poruszające się powietrze?