Wprowadźmy układ współrzędnych o początku w jednym z wierzchołków podstawy akwarium, na przecięciu poziomej osi 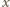 równoległej do
równoległej do 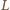 oraz osi
oraz osi 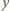 skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny
skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny 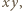 a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej
a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej 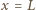 woda podnosi się na wysokość
woda podnosi się na wysokość 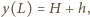 to na ściance
to na ściance 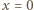 opada do
opada do 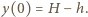 Środek ciężkości wody przesuwa się wówczas z położenia równowagi
Środek ciężkości wody przesuwa się wówczas z położenia równowagi 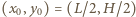 w położenie:
w położenie:
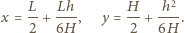
Dla małych drgań przyjmujemy, że 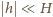 oraz
oraz 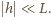 Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego
Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego 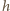 rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną
rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną 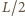 i pionową
i pionową 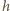 - po stronie
- po stronie 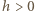 i odejmując taki sam prostopadłościan po stronie
i odejmując taki sam prostopadłościan po stronie 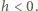 Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
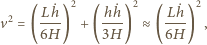
gdzie 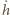 oznacza pochodną
oznacza pochodną 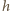 względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa
względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa 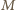 wody porusza się z tą sama prędkością
wody porusza się z tą sama prędkością 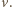 Wówczas zmiany całkowitej energii mechanicznej
Wówczas zmiany całkowitej energii mechanicznej 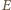 podczas ruchu możemy zapisać jako:
podczas ruchu możemy zapisać jako:
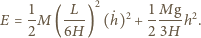
Wyrażenie to "przypomina" nam wzór na energię drgań masy  zawieszonej na sprężynie o stałej sprężystości
zawieszonej na sprężynie o stałej sprężystości 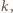 jeśli przyjmiemy:
jeśli przyjmiemy:
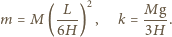
Poszukiwany okres drgań wynosi więc:
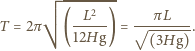
W akwarium o 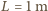 i
i 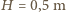
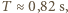 natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć
natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć 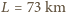 i średnią głębokość
i średnią głębokość 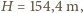 obliczone
obliczone 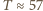 minut (obserwowano fale o
minut (obserwowano fale o 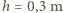 i
i 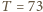 minuty).
minuty).
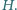 Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości
Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości 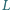 wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z
wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z 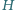 i
i 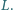 Przyspieszenie ziemskie wynosi
Przyspieszenie ziemskie wynosi 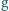 .
.
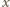 równoległej do
równoległej do 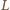 oraz osi
oraz osi 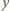 skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny
skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny 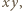 a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej
a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej 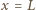 woda podnosi się na wysokość
woda podnosi się na wysokość 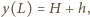 to na ściance
to na ściance 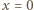 opada do
opada do 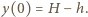 Środek ciężkości wody przesuwa się wówczas z położenia równowagi
Środek ciężkości wody przesuwa się wówczas z położenia równowagi 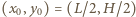 w położenie:
w położenie: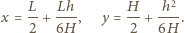
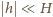 oraz
oraz 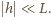 Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego
Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego 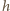 rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną
rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną 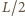 i pionową
i pionową 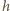 - po stronie
- po stronie 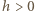 i odejmując taki sam prostopadłościan po stronie
i odejmując taki sam prostopadłościan po stronie  Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc: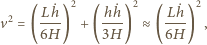
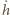 oznacza pochodną
oznacza pochodną 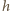 względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa
względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa 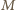 wody porusza się z tą sama prędkością
wody porusza się z tą sama prędkością 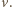 Wówczas zmiany całkowitej energii mechanicznej
Wówczas zmiany całkowitej energii mechanicznej 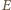 podczas ruchu możemy zapisać jako:
podczas ruchu możemy zapisać jako: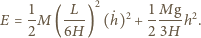
 zawieszonej na sprężynie o stałej sprężystości
zawieszonej na sprężynie o stałej sprężystości 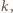 jeśli przyjmiemy:
jeśli przyjmiemy: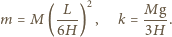
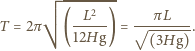
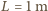 i
i 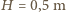
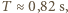 natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć
natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć 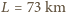 i średnią głębokość
i średnią głębokość 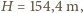 obliczone
obliczone 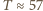 minut (obserwowano fale o
minut (obserwowano fale o 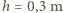 i
i 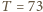 minuty).
minuty).