Klub 44F - zadania I 2016»Zadanie 610
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2016
- Publikacja w Delcie: styczeń 2016
- Publikacja elektroniczna: 1 stycznia 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Mokre koło o promieniu 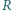 obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi
obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi 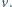 Znaleźć granicę obszaru suchego.
Znaleźć granicę obszaru suchego.



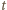 znajdowały się na okręgu o środku w punkcie
znajdowały się na okręgu o środku w punkcie 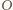 (
(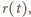 przy czym
przy czym 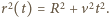 W polu ciężkości środek okręgu obniża się i w czasie
W polu ciężkości środek okręgu obniża się i w czasie 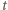 przebywa drogę
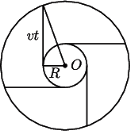
przebywa drogę 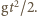 Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili
Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili 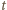 postać:
postać: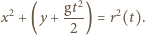
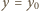 (
(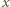 odpowiadającej jednemu z okręgów przecinających tę prostą:
odpowiadającej jednemu z okręgów przecinających tę prostą: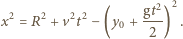
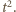 Jego wartość maksymalna
Jego wartość maksymalna 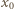 spełnia równanie:
spełnia równanie: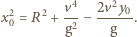
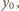 otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru:
otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru: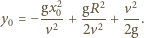
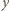 na wysokości
na wysokości 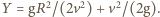 Gdy
Gdy 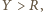 czyli spełniony jest warunek
czyli spełniony jest warunek 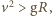 poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (
poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (