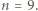Klub 44F - zadania II 2018»Zadanie 653
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania II 2018
- Publikacja w Delcie: luty 2018
- Publikacja elektroniczna: 1 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (112 KB)
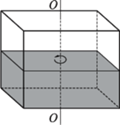
Do wąskiego, prostopadłościennego naczynia nalano pewną ilość cieczy. Następnie naczynie zaczęto obracać wokół pionowej osi symetrii. Przy pewnej prędkości kątowej odsłonięta została 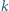 -ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.
-ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.

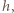 a rozmiary podstawy naczynia przez
a rozmiary podstawy naczynia przez 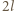 i
i 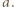 Zgodnie z treścią zadania
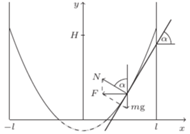
Zgodnie z treścią zadania 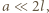 możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.
możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.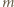 na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości
na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości 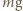 i siła reakcji
i siła reakcji 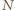 ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości
ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości 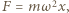 gdzie
gdzie 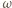 jest prędkością kątową, a
jest prędkością kątową, a 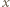 odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem
odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem  i spełnione są związki:
i spełnione są związki: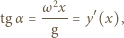
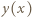 opisuje kształt powierzchni cieczy. Stąd
opisuje kształt powierzchni cieczy. Stąd 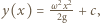 a stałą
a stałą  możemy wyznaczyć z warunków brzegowych. Gdy
możemy wyznaczyć z warunków brzegowych. Gdy 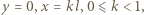 zatem
zatem 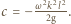 Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się:
Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się: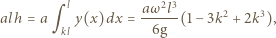
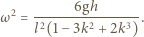
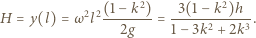
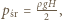 gdzie
gdzie 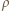 jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest
jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest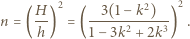
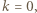 otrzymujemy
otrzymujemy