Przytoczmy eksperyment myślowy Lwa Landaua, który prowadzi do warunku, jaki należy spełnić, aby działy się rzeczy tak niezwykłe, jak brak tarć i oporów. Załóżmy, że mamy pojemnik z płynem, do którego wrzucamy malutką kulkę, masę punktową 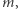poruszającą się z prędkością Zastanawiamy się, czy kulka musi być spowalniana przez ciecz. Wiemy, że obiekty poruszające się w wodzie czy w powietrzu ze względu na lepkość hamują. Lepkość powietrza jest mała, jednak to ona powoduje, że skoczek spadochronowy bezpiecznie ląduje na ziemi. Nawet przed otworzeniem spadochronu prędkość skoczka nie rośnie dowolnie, ale stabilizuje się na około 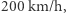w wyniku równowagi między oporami powietrza a siłą grawitacji. Lepkość wody jest znaczna, o czym przekonujemy się, pływając w niej. Na czym właściwie polega to spowalnianie przez lepkość? Zasada zachowania pędu oznacza, że skoro ciało hamuje w płynie, to coś obok powinno przyspieszać. Tym czymś muszą być cząstki płynu. Za lepkością stoi więc mechanizm, w wyniku którego ciało poruszające się w płynie przekazuje jego cząstkom część pędu. Z kolei poruszające się masy niosą ze sobą energię - energię kinetyczną wynikającą z ich ruchu, być może również energię wynikającą z oddziaływań między cząstkami. Nie wchodząc w szczegóły, nazwijmy tę energię dostarczoną do płynu 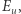gdzie 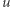niech będzie prędkością, o jaką zwolniła masa punktowa. Tym samym początkowa energia kinetyczna masy to 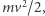a końcowa 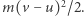Zasada zachowania energii ma postać:

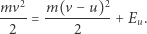Po przekształceniach dostajemy 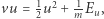co prowadzi do następującego warunku:

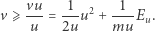(1)

Naiwnie moglibyśmy oczekiwać, że iloraz 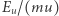może być dowolnie mały. Jeśli np. wzbudzeniem jest cząstka albo grupa cząstek, poruszających się z prędkością 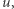wtedy ich energia kinetyczna wynosi: (masa cząstek) 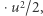a iloraz 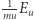pozostanie proporcjonalny do 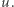Wtedy dla prędkości dążącej do 0 również cały iloraz 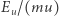znika. Co by się natomiast stało, gdyby te najmniej energetyczne wzbudzenia płynu nie zależały od prędkości jak 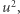ale były do tej prędkości proporcjonalne? Rozważmy hipotetyczną sytuację, w której energia płynu wraz z dostarczanym pędem 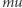rośnie proporcjonalnie do tego pędu, czyli 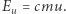Wtedy nierówność (1) prowadzi do warunku:

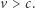(2)

Warunek oznacza, że jeśli masa wrzucona w płyn z taką niezwykłą zależnością energii od prędkości byłaby wolna, wolniejsza niż krytyczna wartość 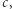to niemożliwym byłoby spełnienie zasady zachowania energii i pędu, zakładając, że płyn zyskał pęd. Innymi słowy, wolne cząstki poruszałyby się w tym płynie tak, jakby tego płynu w ogóle nie było! Tak, jakby wokół była próżnia! Natomiast szybsze cząstki, poruszające się z prędkościami przekraczającymi 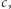mogłyby oddawać energię płynowi, a tym samym zwalniać.

Czy takie płyny z nietypową zależnością energii od prędkości istnieją? Okazuje się, że tak! Płyny takie nazywamy nadciekłymi, a badane są od dekad. Pierwsze doświadczenia, dotyczące nadciekłego helu, przeprowadzone zostały w 1937 roku przez Piotra Kapicę, który za te badania został uhonorowany Nagrodą Nobla (ponad 40 lat później). Odkrycie Kapicy wzbudziło olbrzymie zainteresowanie ówczesnych fizyków teoretycznych, którzy próbowali na różne sposoby zrozumieć to zjawisko. Okazuje się, że ścisły opis jest dość skomplikowany. Wprawdzie wczesne fenomenologiczne modele László Tiszy i Lwa Landaua dawały zgodność jakościową z doświadczeniem, ale na mikroskopijne wyjaśnienia, tzw. ab initio, należało czekać dekady. Nawet kiedy już poznano mechanizmy rządzące nadciekłością, poprawne ilościowe wyniki zaczęto obliczać dopiero w latach 90-tych, kiedy pojawiły się dostatecznie mocne komputery i pogłębiło się zrozumienie teorii układów wielu ciał. Okazuje się, że w bardzo schłodzonych gazach i cieczach, dla dość typowych oddziaływań między cząstkami, energia rośnie proporcjonalnie do prędkości. Rozumowanie z początku tego artykułu prowadzi więc do warunku (2), w którym pojawia się krytyczna prędkość 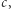będąca przy okazji prędkością rozchodzenia się dźwięku w tych układach. W doświadczeniach nadciekłość jest zjawiskiem bardzo stabilnym - doświadczenia z nadciekłym helem dotyczą litrów płynu, a efekty są tak wyraźne i zaskakujące jak sztuczki magiczne Davida Copperfielda (odsyłacze do nagrań na końcu artykułu).

W trakcie dekad badań pojęcie nadciekłości uległo pewnemu "rozmyciu". Funkcjonują liczne, nierównoważne kryteria nadciekłości. Poniżej omówiono różne ujęcia nadciekłości w kontekście nadciekłych gazów. Samo sformułowanie może wydawać się dziwne - jak gaz ma być nadciekły, skoro nawet nie jest ciekły? Z powyższych rozważań wynika, że nadciekłość dotyczy nie tylko płynów, również gazów, a ma przejawiać się brakiem lepkości lub sił oporu. Nadciekły gaz tak naprawdę był już prezentowany w Delcie - jest to gaz schłodzony do temperatur miliardy razy niższych niż temperatura pokojowa, który przechodzi w tzw. kondensat Bosego-Einsteina. W typowym gazie cząstki poruszają się chaotycznie w losowych kierunkach z losową szybkością. W gazie schłodzonym do kondensatu Bosego-Einsteina wszystkie cząstki mają taką samą, prawie zerową prędkość, do tego na bodźce reagują kolektywnie. Zachowują się tak samo jak żołnierze w trakcie marszu (cytując noblistę Wolfganga Ketterlego). W tym kontekście nie jest to może dziwne, że faza ta jest nadciekła - intuicyjnie wynika ona z regularności ruchu wszystkich atomów. Cząstkom tworzącym kondensat Bosego-Einsteina praktycznie zawsze towarzyszy reszta cząstek, tworząca "zwykłą" chmurę termiczną, złożoną z cząstek o losowych prędkościach, zachowujących się niezależnie. Układ zawiera jakby dwa gazy na raz - nadciekły kondensat oraz fazę normalną. Pierwszy eksperyment demonstrujący nadciekłość gazów wykonała w 2004 roku grupa noblisty Wolfganga Ketterlego, pracującego w Massachusetts Institute of Technology. Kondensat Bosego-Einsteina oświetlono silną wąską wiązką laserową, której położenie i prędkość były precyzyjnie sterowane. Gdy wiązka była przesuwana po kondensacie z prędkością mniejszą niż krytyczna prędkość 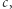która w kondensacie jest rzędu 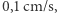wtedy nie obserwowano żadnych zmian w schłodzonym gazie. Dopiero gdy położenie wiązki zmieniano szybciej niż 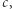w gazie pojawiły się wiry i fale dźwiękowe. Tym samym zrealizowano wprost doświadczenie myślowe przeprowadzone przez Lwa Landaua, opierając się na warunku (2). Warto zwrócić uwagę na pewną subtelność, gdyż możliwe jest zmniejszanie, a nawet wyłączenie, oddziaływań między cząstkami. Kondensat Bosego-Einsteina gazu doskonałego (złożonego z cząstek nieoddziałujących) nie jest nadciekły - przynajmniej nie w sensie kryterium Landaua.

Są inne kryteria nadciekłości, które omówimy na przykładzie płynów umieszczonych w pojemniku w kształcie pierścienia. Jeden z nich dotyczy zachowania płynu, gdy pojemnik, w którym się znajduje, zaczyna się powoli obracać. Płyn przejawia nadciekłość pierwszego rodzaju, gdy nie zaczyna się obracać, mimo że obraca się naczynie, które go utrzymuje. Tego typu nadciekłość ma miejsce nawet w przypadku gazu doskonałego i wynika wprost z ogólnych cech mechaniki kwantowej. Otóż w układzie zamkniętym energie są "skwantowane", tzn. układ może przyjąć tylko pewne wartości energii. Załóżmy, że pojemnik utrzymujący gaz obraca się powoli, z małą prędkością kątową 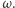Klasyczny płyn obracałby się wraz z pojemnikiem, a cząstki płynu miałyby prędkość proporcjonalną do 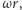gdzie to promień pierścienia. Jeśli jednak odpowiadająca temu energia kinetyczna 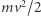jest znacznie mniejsza niż minimalny kwant energii obliczony dla danego układu, to płyn po prostu pozostaje nieruchomy.

Innym kryterium nadciekłości jest istnienie trwałych wirów. Załóżmy, że pojemnik i znajdujący się w nim płyn już się obracają, z taką samą dużą prędkością kątowa. Jak zachowa się ciecz, gdy pojemnik nagle przestanie się obracać? Zwykły, klasyczny obracający się płyn na skutek tarcia o ścianki naczynia i zderzeń między jego cząstkami po chwili zatrzyma się. Inaczej wygląda sprawa, gdy mówimy o płynie nadciekłym. Płyn nadciekły może obracać się niezwykle długo, nie zważając na zatrzymanie się pojemnika. Kondensat Bosego-Einsteina oddziałujących cząstek spełnia to drugie kryterium nadciekłości, co potwierdzono doświadczalnie w eksperymencie przeprowadzonym w grupie Gretchen K. Campbell (National Institute of Standards and Technology). W doświadczeniu kondensat Bosego-Einsteina umieszczono w pułapce o kształcie pierścienia. Z przyczyn technicznych pułapka była nieruchoma, natomiast możliwe było rozkręcenie kondensatu dodatkowym laserem odpychającym atomy. Wiązka lasera obracała się po obwodzie pierścienia, wprawiając atomy w ruch. Przy stopniowym wyłączaniu wiązki obserwowano, że skondensowany gaz porusza się długo po obwodzie pierścienia, analogicznie do nadciekłego helu.

Zainteresowanym Czytelnikom polecam obejrzenie na YouTube nagrań doświadczeń przeprowadzonych na schłodzonych cieczach, konkretnie ciekłym helu. Pierwszy film (youtu.be/2Z6UJbwxBZI) pokazuje doświadczenie, w którym widać, jak nadciekły hel wspina się po ściankach naczynia, pozornie wbrew grawitacji. W drugim filmie (youtu.be/YVMuI_shltE) widać tak zwaną fontannę helową.

W komentarzach pod filmami o nadciekłości pojawia się pytanie - czy w cieczy nadciekłej da się pływać? Z powyższych rozważań wynika, że jak najbardziej - wystarczy machać rękoma szybciej niż prędkość krytyczna nadciekłego płynu. A czy kręcący się bez końca bączek jest zawsze dowodem na to, że śnimy? Jak widać, niekoniecznie: obserwując kręcący się bączek zrobiony z nadciekłego helu, nie będziemy w stanie rozstrzygnąć, czy to jawa czy sen.