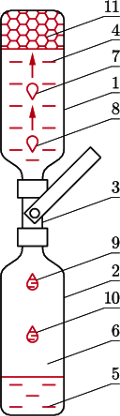
Rys. 1 Budowa przyrządu i obserwowane w nim efekty; 1, 2 – przezroczyste plastikowe butelki, 3 – zawór kulowy, 4, 5 – szampon, 6 – powietrze, 7, 8 – pęcherzyki powietrza, 9, 10 – krople szamponu, 11 – piana.

Górną butelkę należy całkowicie napełnić szamponem (Rys. 1) i bardzo powoli otwierać zawór. W szyjce górnej butelki, tuż nad zaworem, utworzy się pęcherzyk powietrza i będzie się powoli poruszał pionowo w górę (fot. 1), a jednocześnie do dolnej butelki kapnie porcja szamponu. Zmieniając otwarcie zaworu, możemy zbadać, jak wpływa to na rozmiary pęcherzyków, odstęp czasu między ich pojawianiem się oraz ich prędkość, pamiętając, że wielkości te zależeć będą także od rodzaju użytego szamponu, średnicy zastosowanego zaworu i temperatury szamponu. Warto zbadać dokładniej te zależności. Rozmiary pęcherzyka możemy z dobrym przybliżeniem określić przez odczytanie ich na skali linijki przyłożonej do ścianki górnej butelki.

Ruch pęcherzyków możemy zbadać ilościowo. W celu wyznaczenia ich prędkości na bocznej powierzchni górnej butelki odmierzamy i rysujemy wodoodpornym pisakiem odcinek o długości około 20 cm, usytuowany pionowo i zaczynający się nieco nad szyjką butelki. Odcinek ten będzie drogą pokonywaną przez pęcherzyk. Ustawiamy niewielki stopień otwarcia zaworu, żeby wytworzyć pęcherzyk powietrza o rozmiarach kilku milimetrów, i mierzymy czas ruchu pęcherzyka wzdłuż tej drogi, po czym obliczamy prędkość.

Analizując obserwowany efekt od strony teoretycznej, łatwo zauważyć, że na poruszający się pęcherzyk działają dwie główne siły skierowane pionowo. Są to: siła wyporu szamponu 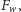 zwrócona do góry, i siła oporu lepkiego 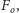 zwrócona w dół. W stanie ustalonym wypadkowa tych sił równa się zeru i pęcherzyk jest w ruchu jednostajnym i prostoliniowym. Siła wyporu jest wprost proporcjonalna do objętości pęcherzyka, a więc do trzeciej potęgi jego promienia, a siła oporu lepkiego wzrasta liniowo wraz z promieniem. Wyjaśnia to, dlaczego większe pęcherzyki osiągają większe prędkości. Dla ścisłości należy dodać, że zaraz po utworzeniu pęcherzyka jego prędkość wzrasta wykładniczo do ustalonej wartości granicznej ruchu jednostajnego, którą wyznaczaliśmy. Przeprowadzone doświadczenia pozwalają także zauważyć, że prędkość ruchu pęcherzyków wzrasta wraz ze wzrostem temperatury szamponu, gdyż współczynnik lepkości, decydujący o wartości siły oporu, maleje wykładniczo ze wzrostem temperatury.

Po kilkunastokrotnym przeprowadzeniu opisanych doświadczeń nad powierzchnią szamponu pojawi się okazała piana (fot 2). Jest ona zbudowana z zamkniętych komórek, rozdzielonych cienkimi warstewkami szamponu, ograniczonymi z dwóch stron błoną powierzchniową. W idealnym przypadku komórki te powinny mieć strukturę zapewniającą minimalizowanie energii swobodnej. Jest ona związana przede wszystkim z napięciem powierzchniowym, a zatem komórki piany powinny być wypełniającymi przestrzeń wielościanami o najmniejszym polu przy ustalonej objętości. W rzeczywistości jednak zdarzają się odstępstwa od tej regularnej struktury, spowodowane m.in. przypadkowymi zaburzeniami podczas wychodzenia pęcherzyków powietrza ponad górną powierzchnię szamponu czy łączeniem się sąsiednich komórek (fot 3).

Rys. 2 Modele komórek piany: (a) Kelvina, (b) Weairego i Phelana.

Zagadnienie znalezienia kształtu komórek piany okazało się fascynującym problemem matematycznym. Kelvin uważał, że rozwiązanie składa się z czternastościanów, takich jak na rysunku 2(a). W 1993 r. Weaire i Phelan znaleźli jednak strukturę mającą pole powierzchni o 0,3% mniejsze, przedstawioną na rysunku 2(b).