---

Rezygnując z próby uwzględnienia całej złożoności drgań liścia, zbudujemy uproszczony jednowymiarowy model tego zjawiska. Jego istotną cechą będzie nieliniowość. W naszym modelu liść jest reprezentowany przez masę  która może przesuwać się wzdłuż poziomej osi  Masa jest częściowo zanurzona w wodzie płynącej z prędkością  w dodatnim kierunku osi  Działa więc na nią siła oporu zależna od prędkości masy względem wody,  która powoduje wychylenie masy z położenia równowagi  Wychyleniu temu przeciwdziała siła sprężysta równa  Równanie ruchu masy ma postać

Dla dalszych rozważań podzielimy obie strony przez 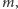 otrzymując

(*)

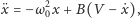gdzie 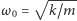 oraz 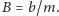 Istotne znaczenie ma fakt, że współczynnik 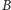 nie jest stały, ponieważ zależy od głębokości, na jaką liść się zanurza. Głębokość ta zmienia się, ponieważ wychylenia w poziomie wpływają na położenie liścia w pionie, tak że w rzeczywistości zatacza on zamkniętą krzywą o owalnym kształcie. Widać więc, że współczynnik oporu należałoby uzależniać od pionowej współrzędnej liścia, co wymagałoby rozpatrywania ruchu przynajmniej w dwóch wymiarach. Można jednak zauważyć, że zmiany głębokości zanurzenia mają podobny przebieg w czasie, jak zmiany poziomej prędkości liścia. Wykorzystamy to podobieństwo w naszym jednowymiarowym modelu i wyrazimy współczynnik oporu jako funkcję

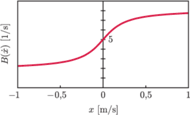
Rys. 1

Kształt funkcji 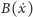 pokazany na rysunku 1 uwzględnia fakt, że zmiany współczynnika 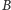 mają ograniczony zakres, nawet gdy prędkość osiąga duże wartości. W naszym modelu dla analitycznego przedstawienia funkcji 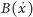 wykorzystamy – dość dowolnie – funkcję arcus tangens:

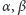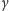gdzie  i   są stałymi. Z powodu zależności współczynnika 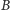 od 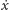 równanie 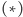 jest nieliniowe i niemożliwe do analitycznego rozwiązania. Jednak to dzięki zmienności 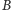 dochodzi do rozkołysania liścia. Gdy bowiem zrezygnujemy z niej, przyjmując 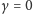 lub 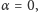 czyli 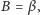 dostajemy liniowe równanie różniczkowe

(**)

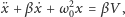które przewiduje, że po nieskończenie długim czasie ruch zamiera. Odpowiednie rozwiązanie ma postać zależną od relacji między 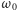 a wielkością 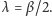 Gdy 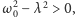 opisuje ono drgania o częstości

zanikające w położeniu równowagi

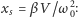
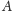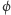gdzie  i   są stałymi zależnymi od warunków początkowych.

W przeciwnym przypadku rozwiązanie przewiduje aperiodyczny ruch także zmierzający do 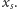 (Oczywiście proporcjonalność 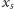 do  jest ograniczona do prędkości prądu, przy których liść nie łamie się i nie niszczy.)

Aby zbadać charakter rozwiązań nieliniowego równania 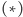 uwzględniającego 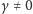 i 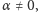  rozważmy małe wychylenia 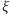 z położenia :

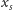Wykorzystując fakt, że prędkości 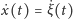 również są małe, można użyć przybliżenia

Pomijamy też pojawiający się w równaniu 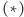 składnik z 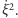  W efekcie otrzymujemy znów rozwiązywalne równanie liniowe

Jego rozwiązanie ma cechy podobne do rozwiązania równania 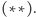 W szczególności gdy

zawiera ono czynnik wykładniczy, tym razem z wykładnikiem 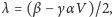 którego znak zależy od prędkości prądu:

W wodzie stojącej lub płynącej leniwie współczynnik 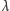 jest dodatni i kołysanie liścia ustaje. Jednak gdy prędkość nurtu przekracza wartość krytyczną 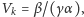 czynnik wykładniczy rośnie z czasem, co odpowiada wahaniom narastającym.

Rys. 2

(Stosownie do upraszczających założeń poczynionych przy wyprowadzeniu równania  wynik ten jest poprawny tylko dla małych drgań, więc nie należy przywiązywać wagi do sugerowanego funkcją eksponencjalną wzmagania się drgań w nieskończoność.)

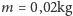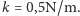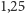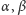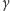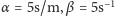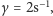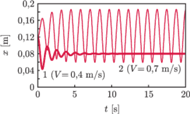
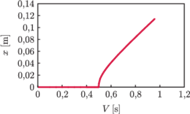
Pora teraz na – numeryczne z konieczności – rozwiązanie pełnego nieliniowego równania ruchu  Trzeba tylko ustalić w miarę realistyczne wartości parametrów układu. Rozsądne wydaje się przyjęcie  i  Swobodny liść kołysze się wtedy z okresem około  s. Parametry  i   można dobrać tak, aby ruch wyglądał jak najbardziej prawdopodobnie, np.  i   co daje prędkość krytyczną około  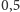m/s. Przykłady rozwiązań  przedstawione są na rysunku 2

Rys. 3

Liść zanurzony w powoli płynącym potoku nie kołysze się trwale – początkowo wychylony szybko uspokaja się (krzywa 1). W bystrzejszym nurcie równie szybko ustalają się znaczne wahania (krzywa 2). Rysunek 3 przedstawia zależność ich amplitudy od prędkości wody.

Progowy charakter wzbudzenia drgań jest wyraźnie widoczny. Energia rozkołysanego liścia pochodzi z niewyczerpalnego praktycznie źródła, jakim jest przepływ wody.

Rys. 4

Z powyższej analizy wynika, że jeśli prędkość prądu jest mała, to istnieje położenie równowagi, w którym liść spoczywa i do którego asymptotycznie zmierza po dowolnym wychyleniu. Takie dążenie można przedstawić w płaszczyźnie  – tak zwanej przestrzeni fazowej (Rys. 4).

Punkt równowagi osiągany po długim czasie jest przykładem atraktora zwanego ogniskiem. „Przyciąga” on stany układu zadane dowolnymi warunkami początkowymi (krzywa 1). Jeśli natomiast prędkość wody przewyższa krytyczną, to wspomniane położenie równowagi przestaje istnieć. W jego miejsce pojawia się atraktor w postaci zamkniętej krzywej zwany cyklem granicznym. Tory na płaszczyźnie fazowej zbliżają się do niego od wewnątrz (jak krzywa 2) lub z zewnątrz (jak krzywa 3), zależnie od warunków początkowych.

Zachowanie układu polegające na zastąpieniu punktu stałego cyklem granicznym odpowiadającym ruchowi okresowemu wskutek zmiany parametrów układu nosi nazwę bifurkacji Hopfa. Bifurkacja Hopfa jest często spotykana w zachowaniu nieliniowych układów fizycznych, chemicznych i biologicznych. Praktyczne znaczenie ma np. bifurkacja prowadząca do wzbudzania wibracji skrzydła samolotu lub wału turbiny, co może mieć katastrofalne następstwa. Kołysanie liścia lepiężnika jest niegroźnym przypadkiem, do którego obserwacji zachęcam miłośników górskiej przyrody.