Jak to działa?
Fizyka w szklance piwa
Każdy z Was, Drodzy Czytelnicy, obserwował kiedyś pęcherzyki gazu unoszące się do góry w szklance wypełnionej świeżym, chłodnym piwem (alkohol szkodzi zdrowiu!!!). Podobne zjawisko można zobaczyć w szklance z wodą sodową – dla ustalenia uwagi pozostaniemy jednak przy piwie. Postaramy się opisać tutaj wzrost i ruch bąbelków.

Jak wiadomo, piwo jest nasycone dwutlenkiem węgla. Dopóki jest ono
zamknięte w butelce (choć niektórzy wolą piwo z puszki) pod zwiększonym
ciśnieniem, nic ciekawego się nie dzieje. Jednak w momencie gdy ją otworzymy,
ciśnienie w butelce zmniejsza się na tyle, że
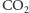 uwalnia się w postaci
pęcherzyków tworzących się na dnie i ściankach szklanki. Piwo, zaraz po
otwarciu butelki znajduje się w stanie niestabilnym. Właśnie zmiana ciśnienia
powoduje, że
uwalnia się w postaci
pęcherzyków tworzących się na dnie i ściankach szklanki. Piwo, zaraz po
otwarciu butelki znajduje się w stanie niestabilnym. Właśnie zmiana ciśnienia
powoduje, że
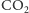 „woli” przechodzić w stan gazowy niż pozostawać
rozpuszczone w piwie. Bąbelki tworzą się na drobnych nierównościach na
powierzchni szklanki (to trochę tak, jak para wodna w chmurach kondensuje się
na pyłkach znajdujących się w powietrzu i spada w postaci deszczu). Można
sprawdzić, że po wsypaniu do szklanki, na przykład, pieprzu (!) lub cukru
(już lepiej) szybkość powstawania bąbelków znacznie wzrasta. Na początku
pęcherzyki rosną przyklejone do ścianek, dopiero gdy działająca na
nie siła wyporu stanie się większa niż siła napięcia powierzchniowego
utrzymująca je przy ściance, odrywają się i wędrują do góry. Wyobraźcie
sobie, że problem bąbelków w piwie jest traktowany na tyle poważnie,
że dwóch chemików ze Stanford University, Neil Shafer i Richard Zare,
przeprowadziło doświadczenia, w których zmierzyli szybkość powiększania
się pęcherzyków w miarę wznoszenia i zależność ich położenia od czasu.
Spróbujmy zbudować model opisujący wzrost bąbelków, a nieco później
zastanowimy się nad ich ruchem ku powierzchni. Dzięki wspomnianym
chemikom będziemy w stanie porównać przewidywania modelu z danymi
doświadczalnymi.
„woli” przechodzić w stan gazowy niż pozostawać
rozpuszczone w piwie. Bąbelki tworzą się na drobnych nierównościach na
powierzchni szklanki (to trochę tak, jak para wodna w chmurach kondensuje się
na pyłkach znajdujących się w powietrzu i spada w postaci deszczu). Można
sprawdzić, że po wsypaniu do szklanki, na przykład, pieprzu (!) lub cukru
(już lepiej) szybkość powstawania bąbelków znacznie wzrasta. Na początku
pęcherzyki rosną przyklejone do ścianek, dopiero gdy działająca na
nie siła wyporu stanie się większa niż siła napięcia powierzchniowego
utrzymująca je przy ściance, odrywają się i wędrują do góry. Wyobraźcie
sobie, że problem bąbelków w piwie jest traktowany na tyle poważnie,
że dwóch chemików ze Stanford University, Neil Shafer i Richard Zare,
przeprowadziło doświadczenia, w których zmierzyli szybkość powiększania
się pęcherzyków w miarę wznoszenia i zależność ich położenia od czasu.
Spróbujmy zbudować model opisujący wzrost bąbelków, a nieco później
zastanowimy się nad ich ruchem ku powierzchni. Dzięki wspomnianym
chemikom będziemy w stanie porównać przewidywania modelu z danymi
doświadczalnymi.
Dlaczego pęcherzyki rosną?
Naiwnie narzucająca się odpowiedź brzmi: w miarę oddalania się od dna
szklanki maleje ciśnienie hydrostatyczne (piwostatyczne), bąbelki są słabiej
ściskane i dzięki temu rośnie ich objętość. Po chwili zastanowienia
zauważymy jednak, że jest to wyjaśnienie błędne. Na powierzchni piwa
panuje ciśnienie atmosferyczne 1 atm. Jak łatwo zauważyć gołym okiem,
pęcherzyki wędrujące od dna do powierzchni zwiększają swoje rozmiary mniej
więcej 2-krotnie (objętość rośnie
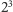 -krotnie). Z równania gazu
doskonałego wiemy, że
-krotnie). Z równania gazu
doskonałego wiemy, że
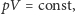 zatem 8-krotne zwiększenie
objętości nastąpiłoby pod wpływem tyleżkrotnego zmniejszenia ciśnienia.
Ponieważ na powierzchni ciśnienie jest równe 1 atm, zatem na dnie szklanki
musielibyśmy mieć aż 8 atm! Naturalnie jest to możliwe, ale taki kufel
musiałby mieć około 80 m wysokości (piękny widok!). Musimy zatem takie
rozwiązanie odrzucić.
zatem 8-krotne zwiększenie
objętości nastąpiłoby pod wpływem tyleżkrotnego zmniejszenia ciśnienia.
Ponieważ na powierzchni ciśnienie jest równe 1 atm, zatem na dnie szklanki
musielibyśmy mieć aż 8 atm! Naturalnie jest to możliwe, ale taki kufel
musiałby mieć około 80 m wysokości (piękny widok!). Musimy zatem takie
rozwiązanie odrzucić.
Jak wiemy, bąbelki to dwutlenek węgla rozpuszczony w piwie, który po
otwarciu butelki uwalnia się w postaci gazu. To właśnie kosztem nadmiaru
(w warunkach zmniejszonego ciśnienia po otwarciu butelki)
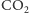 w piwie następuje przyrost objętości pęcherzyków, stanowią one „centra
parowania”: całą swoją powierzchnią pochłaniają dwutlenek węgla rozpuszczony
w piwie. W oparciu o to spostrzeżenie zbudujemy prosty model bąbelka oparty
na następujących założeniach:
w piwie następuje przyrost objętości pęcherzyków, stanowią one „centra
parowania”: całą swoją powierzchnią pochłaniają dwutlenek węgla rozpuszczony
w piwie. W oparciu o to spostrzeżenie zbudujemy prosty model bąbelka oparty
na następujących założeniach:
- 1.
- bąbelki są kuliste,
- 2.
- ciśnienie hydrostatyczne jest stałe (poprzednie rozważania pozwalają przyjąć to założenie, przynajmniej przy opisie doświadczeń wykonanych przy użyciu szklanek o normalnych rozmiarach),
- 3.
- szybkość pochłaniania
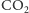 jest wprost proporcjonalna do
powierzchni pęcherzyka:
jest wprost proporcjonalna do
powierzchni pęcherzyka:
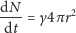
(1) gdzie
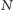 jest liczbą cząsteczek
jest liczbą cząsteczek
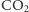 w pęcherzyku,
w pęcherzyku,
 jego
promieniem, a
jego
promieniem, a
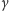 stałym współczynnikiem proporcjonalności,
stałym współczynnikiem proporcjonalności,
- 4.
- dodatkowo zakładamy, że ciśnienie
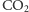 spowodowane istnieniem
napięcia powierzchniowego można pominąć,
spowodowane istnieniem
napięcia powierzchniowego można pominąć,
- 5.
- temperatura w szklance jest stała.
Zakładając w dodatku, że
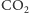 w pęcherzyku spełnia równanie gazu
doskonałego:
w pęcherzyku spełnia równanie gazu
doskonałego:
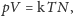 gdzie
gdzie
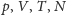 to ciśnienie, objętość,
temperatura i liczba cząsteczek
to ciśnienie, objętość,
temperatura i liczba cząsteczek
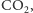 a
a
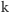 – stała Boltzmanna,
dostajemy
– stała Boltzmanna,
dostajemy
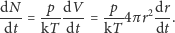 | (2) |
Korzystając z założenia 3. otrzymujemy proste równanie
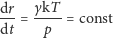 | (3) |
skąd
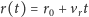 | (4) |
dla
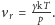 Uwzględnienie napięcia powierzchniowego prowadziłoby do
pojawienia się w ostatnim równaniu dodatkowego wyrazu proporcjonalnego do
Uwzględnienie napięcia powierzchniowego prowadziłoby do
pojawienia się w ostatnim równaniu dodatkowego wyrazu proporcjonalnego do
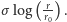
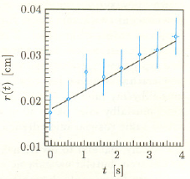
Rys. 1 Promień unoszącego się bąbelka w zależności od czasu.
Chemicy, o których wspominałem, przeprowadzili pomiary zależności promienia pęcherzyka od czasu. Okazało się, że przedstawiony powyżej model świetnie opisuje dane doświadczalne przedstawione na rysunku 1.
Ruch bąbelków
Teraz spróbujemy odpowiedzieć na pytanie, jak zmienia się w czasie
położenie pęcherzyka
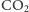 w szklance z piwem. Najpierw znajdziemy
siły działające na pęcherzyk. Pierwsza z nich to siła wyporu pomniejszona
o ciężar pęcherzyka, równa, zgodnie z prawem Archimedesa:
w szklance z piwem. Najpierw znajdziemy
siły działające na pęcherzyk. Pierwsza z nich to siła wyporu pomniejszona
o ciężar pęcherzyka, równa, zgodnie z prawem Archimedesa:
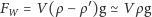 | (5) |
gdzie
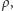
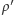 to gęstość piwa i gęstość
to gęstość piwa i gęstość
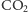 w pęcherzyku,
a
w pęcherzyku,
a
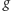 jest przyspieszeniem ziemskim. Pominięcie
jest przyspieszeniem ziemskim. Pominięcie
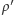 po prawej
stronie powyższego wzoru jest uzasadnione. Załóżmy teraz dodatkowo,
że prędkość ruchu pęcherzyków jest na tyle mała, że podczas ruchu
zachowują one kształt sferyczny. Przy dużych prędkościach założenie to
przestaje być słuszne, a z kul robią się poziomo spłaszczone dyski. Naturalnie,
jak to w fizyce bywa, nie będziemy rozważać tego trudnego, realistycznego
przypadku, lecz ograniczymy się do rozpatrzenia sytuacji, gdy bąbelki zachowują
kształt sferyczny.
po prawej
stronie powyższego wzoru jest uzasadnione. Załóżmy teraz dodatkowo,
że prędkość ruchu pęcherzyków jest na tyle mała, że podczas ruchu
zachowują one kształt sferyczny. Przy dużych prędkościach założenie to
przestaje być słuszne, a z kul robią się poziomo spłaszczone dyski. Naturalnie,
jak to w fizyce bywa, nie będziemy rozważać tego trudnego, realistycznego
przypadku, lecz ograniczymy się do rozpatrzenia sytuacji, gdy bąbelki zachowują
kształt sferyczny.
Podczas ruchu pęcherzyka, oprócz siły wyporu i ciężkości, działa na niego
również siła oporu, a jej prawidłowy opis to najtrudniejszy punkt naszych
rozważań. Zauważmy najpierw, że bąbelki poruszają się coraz szybciej;
widocznie siła oporu rośnie wolniej niż siła wyporu
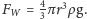 Do opisu siły oporu posłużymy się tzw. prawem Stokesa, które mówi,
że siła oporu działająca na sztywną kulę poruszającą się w nieskończonym,
lepkim ośrodku wynosi
Do opisu siły oporu posłużymy się tzw. prawem Stokesa, które mówi,
że siła oporu działająca na sztywną kulę poruszającą się w nieskończonym,
lepkim ośrodku wynosi
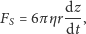 | (6) |
gdzie
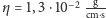 to współczynnik lepkości,
to współczynnik lepkości,
 – promień
kulki, a
– promień
kulki, a
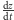 – jej prędkość.
– jej prędkość.
Zakładając, że
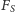 opisuje siłę oporu działającą na pęcherzyk, jesteśmy
teraz w stanie napisać równanie
opisuje siłę oporu działającą na pęcherzyk, jesteśmy
teraz w stanie napisać równanie
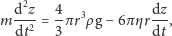 | (7) |
gdzie
 oznacza pionową współrzędną bąbelka, natomiast
oznacza pionową współrzędną bąbelka, natomiast
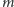 dane
jest wzorem
dane
jest wzorem
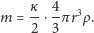 | (8) |
Zauważmy, że dla
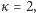
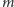 jest masą piwa (!) zawartą w kuli
o rozmiarach pęcherzyka. W zasadzie, zamiast
jest masą piwa (!) zawartą w kuli
o rozmiarach pęcherzyka. W zasadzie, zamiast
 powinniśmy wstawić
tam masę pęcherzyka
powinniśmy wstawić
tam masę pęcherzyka
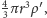 musimy jednak pamiętać, że obiekt
poruszający się w lepkim ośrodku „ciągnie” za sobą „przylepioną” do siebie
ciecz. W porównaniu z nią rzeczywistą masę
musimy jednak pamiętać, że obiekt
poruszający się w lepkim ośrodku „ciągnie” za sobą „przylepioną” do siebie
ciecz. W porównaniu z nią rzeczywistą masę
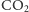 w bąbelku można
pominąć. Właśnie dlatego w równaniu ruchu (7) pominęliśmy masę
w bąbelku można
pominąć. Właśnie dlatego w równaniu ruchu (7) pominęliśmy masę
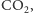 a wprowadziliśmy sparametryzowaną wzorem (8) tę dodatkową,
„przylepioną” masę piwa.
a wprowadziliśmy sparametryzowaną wzorem (8) tę dodatkową,
„przylepioną” masę piwa.
Współczynnik
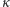 wprowadziliśmy po to, by sprawdzić, jak silnie ruch
pęcherzyka zależy od wielkości „przylepionej” masy. Znalezione przez nas
równanie daje się przepisać w wygodniejszej postaci:
wprowadziliśmy po to, by sprawdzić, jak silnie ruch
pęcherzyka zależy od wielkości „przylepionej” masy. Znalezione przez nas
równanie daje się przepisać w wygodniejszej postaci:
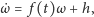 | (9) |
gdzie
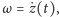
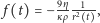
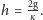 Standardowe metody
rozwiązywania równań różniczkowych (zamiana zmiennych i uzmiennianie
stałej) prowadzą do następującego wyrażenia
Standardowe metody
rozwiązywania równań różniczkowych (zamiana zmiennych i uzmiennianie
stałej) prowadzą do następującego wyrażenia
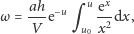 | (10) |
gdzie
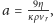 a
a
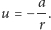
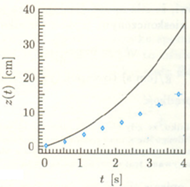
Rys. 2 Położenie bąbelków w zależności od czasu: diamenciki – dane doświadczalne,linia ciągła – przewidywanie modelu.
Kolejne całkowanie doprowadza nas do wyrażenia na położenie w zależności od czasu
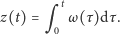 | (11) |
Wyrażenie to można łatwo scałkować na kalkulatorze czy komputerze.
Jednak zamiast pracowitego całkowania można również pomyśleć
i zauważyć, że o ile
 nie jest za duże (okazuje się, że to znaczy nie
większe niż
nie jest za duże (okazuje się, że to znaczy nie
większe niż
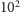 ), to w równaniu ruchu można pominąć wyraz
), to w równaniu ruchu można pominąć wyraz
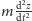 w porównaniu z pozostałymi, a wtedy równanie daje się łatwo
rozwiązać:
w porównaniu z pozostałymi, a wtedy równanie daje się łatwo
rozwiązać:
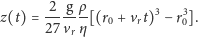 | (12) |
Numeryczne całkowanie równań może nas upewnić, że o ile
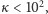 to powyższe równanie bardzo dobrze przybliża dokładne rozwiązanie
równania ruchu.
to powyższe równanie bardzo dobrze przybliża dokładne rozwiązanie
równania ruchu.
Wprawdzie udało nam się rozwiązać równanie ruchu, ale nie nasz wyjściowy problem. Jak widzimy bowiem z rysunku 2, tym razem nasza „teoria” (linia ciągła) nie opisuje prawidłowo danych doświadczalnych. W rzeczywistości pęcherzyk porusza się znacznie wolniej, niż to przewiduje nasze rozwiązanie; siła oporu musi być zatem większa od danej przez prawo Stokesa. Zanim zostawię Cię, Drogi Czytelniku, z tym fundamentalnym problemem, przypomnijmy sobie, jakie założenia są robione przy wyprowadzeniu prawa Stokesa i zastanówmy się, czy przystają one do naszej bąbelkowej rzeczywistości:
- kulka jest sztywna – tymczasem nasz pęcherzyk rośnie, więc sztywny nie jest,
- prędkość (jej styczna i prostopadła składowa) na powierzchni kulki znika (ciecz nie wnika do wnętrza kulki, a z powodu lepkości nie płynie również po jej powierzchni) – w naszym przypadku składowa styczna prędkości piwa na powierzchni pęcherzyka mogłaby być różna od zera,
- ciecz jest nieskończona – tymczasem nasze piwo zawiera się w szklance.
Teraz już, Drogi Czytelniku, po uświadomieniu sobie naszych słabości zostawiam Cię, życząc wielu udanych eksperymentów i znalezienia prawidłowego modelu opisującego ruch bąbelków w piwie.
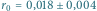 cm, prędkość
cm, prędkość
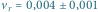 cmś). Możemy
powiedzieć, że nasz prosty model bardzo dobrze opisuje wyniki doświadczalne.
cmś). Możemy
powiedzieć, że nasz prosty model bardzo dobrze opisuje wyniki doświadczalne.
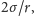 gdzie
gdzie
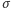 jest stałym współczynnikiem napięcia
powierzchniowego. Widać stąd, że dla
jest stałym współczynnikiem napięcia
powierzchniowego. Widać stąd, że dla
 bardzo małego (zgadnij sam,
co to znaczy, Drogi Czytelniku) ten efekt może być istotny. Jeśli ograniczymy
rozważania do bąbelków średnich rozmiarów (tak jak tutaj), to można
przyjąć, że efekty związane ze zmianą napięcia powierzchniowego są
pomijalne. W rzeczywistości jednak efektywnie uwzględniamy napięcie
powierzchniowe zakładając kulistość bąbelków.
bardzo małego (zgadnij sam,
co to znaczy, Drogi Czytelniku) ten efekt może być istotny. Jeśli ograniczymy
rozważania do bąbelków średnich rozmiarów (tak jak tutaj), to można
przyjąć, że efekty związane ze zmianą napięcia powierzchniowego są
pomijalne. W rzeczywistości jednak efektywnie uwzględniamy napięcie
powierzchniowe zakładając kulistość bąbelków.
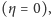 to
to
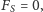 co jest na pierwszy rzut oka niezgodne z naszą intuicją. Jest to
jednak zupełnie niezła intuicja, gdyż dość rzadko (nigdy) mamy do czynienia
z nielepkim przepływem, taka nielepka woda nazywana jest czasami suchą
wodą.
co jest na pierwszy rzut oka niezgodne z naszą intuicją. Jest to
jednak zupełnie niezła intuicja, gdyż dość rzadko (nigdy) mamy do czynienia
z nielepkim przepływem, taka nielepka woda nazywana jest czasami suchą
wodą.