Analiza Stowarzyszenie na rzecz Edukacji Matematycznej
-
-
Twierdzenie Cevy
W wielu zadaniach dane są trzy proste, które albo przecinają się w jednym punkcie, albo należy to o nich udowodnić. Wygodnym narzędziem bywa wtedy twierdzenie Cevy.
-
Wzór Eulera i balony
Polski namiot na francuskim Festiwalu Nauki był tak pełen gości, że miejsce dla jego matematycznej części życzliwie zostało ofiarowane przez Jeana Brette’a i jego kolegów w namiocie Pałacu Odkryć.
-
Jak się mierzy objętość nitką?
Czy przyszło Wam kiedyś do głowy, drodzy Czytelnicy, mierzyć nitką objętość? Albo pole?
-
Analiza niestandardowa
W matematyce, z jaką spotykamy się w szkole i na uniwersytecie, linię prostą identyfikuje się ze zbiorem punktów, w którym współrzędnymi są liczby rzeczywiste. Istnieje jednakże argument przeciw takiemu konkretnemu utożsamieniu, który opiera się na tym, iż nieskończenie wiele własności linii prostej nie może być ani dowiedzionych, ani obalonych za pomocą aksjomatów używanych w teorii mnogości (tzw. aksjomatów Zermelo–Fraenkla).
-

Teoria węzłów Ogródek Gardnera
Poliboromeusze
Matematycy wiedzą, że zabawy ze sznurkiem mogą być źródłem różnych zadań i problemów matematycznych, często bardzo poważnych, o daleko idących konsekwencjach.
-
Jaka to liczba?
Na ogół matematycy nie są ulubionymi gośćmi na przyjęciach. Poprzedza nas reputacja nudziarzy, zanurzonych myślami w definicjach i twierdzeniach. A jednak możemy użyć naszej wiedzy, by oczarować zebranych magicznymi trikami, opartymi na własnościach matematycznych. Może przy okazji ktoś zainteresuje się matematyką?
-
Lehmus, Steiner, Gardner
Powszechnie znany jest fakt, że w trójkącie równoramiennym dwie dwusieczne mają równe długości, podobnie jak dwie wysokości i dwie środkowe. Naturalne jest pytanie: a odwrotnie, czy równość dwóch ze wspomnianych wielkości gwarantuje równoramienność trójkąta?
-
Największa liczba na świecie
Ludzie od niepamiętnych czasów prześcigali się w biciu rekordów w najprzeróżniejszych dziedzinach, od czysto sportowych (szybciej, wyżej, mocniej), poprzez cywilizacyjne (wyższe budowle, większe samoloty, szybsze komputery), aż po całkiem absurdalne, żeby nie powiedzieć głupie.
-
Stereometria Kącik przestrzenny
Czworościany ortocentryczne
Tym razem, zgodnie z obietnicą, kącik poświęcimy czworościanom ortocentrycznym. Jak wiadomo, nie w każdym czworościanie istnieje punkt przecięcia wszystkich wysokości. Czworościany mające taki punkt nazywane są ortocentrycznymi. Spróbujmy opisać je dokładniej.
-
_thumb_100px.jpg)
Wikipedia
Grigorij Jakowlewicz Perelman
Hipoteza Poincarégo
11 listopada 2002 roku Grigorij Jakowlewicz Perelman, geometra pracujący w Petersburskim Oddziale Instytutu Matematycznego im. Stiekłowa przy Fontance 27, udostępnił w Internecie 40-stronicową pracę pod tytułem „Formuła entropii dla potoku Ricciego i jej zastosowania geometryczne”. Czwartą stronę suchego i najeżonego fachowymi terminami wprowadzenia kończy zdanie:
Wreszcie, w rozdziale 13, podajemy krótki szkic dowodu hipotezy geometryzacyjnej. -
Można zacząć od banknotu
Na ile sposobów można przykryć banknotem prostokąt o tych samych rozmiarach? xxx Każdy od razu zgadnie, że na cztery sposoby: do góry orłem, przy czym orzeł może być do dołu lub do góry nogami, i podobnie na dwa sposoby królem do góry (choć na banknocie nie widać jego nóg).
-
Przestrzenie ilorazowe, czyli sklejanie kartki papieru
Do czego może doprowadzić sklejanie kartki papieru?
-
Liczmy oszczędniej
-
Dobra dekada dla liczb pierwszych
Oto spektakularne wyniki z lat 1997–2009, dotyczące liczb pierwszych.
-
Reguła czy przypadek?
Gdy do wielomianu
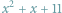 podstawiać będziemy kolejno liczby
podstawiać będziemy kolejno liczby
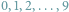 , otrzymamy
, otrzymamy
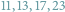 ,
,
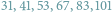 – same
liczby pierwsze. Reguła czy przypadek?
– same
liczby pierwsze. Reguła czy przypadek?
-
Dobrze się składa
Jednokładności były tematem styczniowego deltoidu. Jak każde przekształcenia, jednokładności można składać. Mimo, że wynik takiego złożenia nie musi być jednokładnością, to jednak jednokładności składają się dobrze.
-
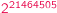 , czyli jeszcze raz o potęgach dwójki
, czyli jeszcze raz o potęgach dwójkiO potęgach dwójki i własnościach ich rozwinięć dziesiętnych można było w Delcie poczytać wielokrotnie, m.in. w artykułach Zbigniewa Marciniaka i wyżej podpisanego. Istnieją zapewne osoby, które nie czytały tych artykułów, dlatego że kilkanaście lat temu nie umiały jeszcze czytać, choć dziś Deltę czytują. Być może jest to dostatecznym usprawiedliwieniem, żeby napisać o całej sprawie jeszcze raz.
-
Liczby zespolone w geometrii
Geometryczną interpretacją ciała liczb zespolonych jest płaszczyzna. Za pomocą liczb zespolonych można opisywać własności figur i przekształceń na płaszczyźnie. Oto kilka przykładów takich zastosowań...
-
Rapsodia pajęcza