Delta mi!

Ktoś mi kiedyś powiedział o zadaniach geometrycznych: Jeśli nie wiesz, co zrobić, narysuj równoległobok! Jakkolwiek żartobliwa i niepoważna może się ta porada wydawać, jednak czasem działa. Oto kilka przykładów.

Historia twierdzenia o czterech barwach sięga roku 1852, kiedy to student Francis Guthrie, wiedziony czysto praktycznymi pobudkami, postawił swemu wykładowcy, Augustowi De Morganowi, następujące pytanie: jaka jest najmniejsza liczba kolorów, która wystarcza do pokolorowania dowolnej płaskiej mapy w taki sposób, aby każde dwa państwa, które graniczą ze sobą, otrzymały różne kolory?

Piraci mają łup w postaci 100 dukatów i muszą go podzielić. Postanowili urządzić podział następująco...

Pojęcie symetrii przydaje się w rachunku prawdopodobieństwa. Oto kilka przykładów...

Jak pokazać, że istnieje obiekt o pewnych własnościach? Najprościej jest podać bezpośrednią konstrukcję, jednak często jest to bardzo trudne (a czasem w ogóle niewykonalne). Jednym ze sposobów ominięcia tego problemu jest tak zwana metoda probabilistyczna...

Na pierwszym etapie tegorocznej Olimpiady Matematycznej pojawiło się poniższe zadanie 1 o numerowaniu krawędzi dwunastościanu. Spośród licznych zadań o podobnej tematyce prezentujemy kilka o dość różnorodnych rozwiązaniach.

W dniu 8 stycznia 2011 roku odbyły się zawody II stopnia VI Olimpiady Matematycznej Gimnazjalistów, w których uczestniczyło 669 uczniów. Spośród nich 187 zostało zakwalifikowanych do zawodów stopnia III.

Rachunek prawdopodobieństwa jest tą dziedziną matematyki, w której istnieje szczególnie dużo paradoksów. Związane jest to z naszymi błędnymi wyobrażeniami o losowości.

W artykule „Gra w 20 pytań” omówiliśmy sposób gry z graczem, który nie kłamie. A jak postępować z graczem, który kłamie? Czy jesteśmy zupełnie bezradni?

... to dobrze znana gra.

Każdy uczeń szkoły średniej wie, że gdy zna się współczynniki trójmianu kwadratowego, to można jawnymi wzorami wyrazić pierwiastki tego trójmianu. We wzorach tych wykonuje się (skończoną liczbę razy) tylko cztery działania arytmetyczne i pierwiastkowanie.

Cóż prostszego, jak stworzyć zbiór z dowolnych prawdziwych lub wymyślonych obiektów! Czyż zbiór nie jest po prostu pewną konstrukcją myślową? Wystarczy zatem pomyśleć o owych obiektach jako o elementach jednego zbioru – i już.

Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry, udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia, informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie płaszczyzny zespolonej

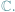
Płaszczyznę 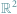można wyposażyć w działania dodawania i mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią ?

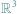Jeśli liczba naturalna 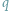jest największą liczbą pierwszą, to...

Dla każdej liczby naturalnej 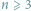można, oczywiście, narysować wielokąt, który ma 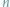 boków. A jak to będzie z wielościanami o zadanej z góry liczbie krawędzi?

Czasami, gdy zbytnio bujamy w obłokach, słyszymy od innych zejdź na ziemię! Kto by pomyślał, że ta zazwyczaj dość nieprzyjemna uwaga może być niekiedy cenną wskazówką do zadań ze stereometrii.

Jak wiadomo, pochodna opisuje zmiany danej wielkości (np. tak działa prędkościomierz w samochodzie). Z kolei całka opisuje sytuację odwrotną – odtwarza daną wielkość z jej zmienności (tak np. działa licznik energii elektrycznej).

W wielu zadaniach dane są trzy punkty, które albo są współliniowe, albo należy to o nich udowodnić. Wygodnym narzędziem bywa wtedy Twierdzenie Menelaosa.