-
-
Niewymierność
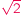 i jeszcze większe niemożliwości
i jeszcze większe niemożliwościPunktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta mianowicie, że liczba
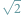 jest niewymierna...
jest niewymierna...
-

Wikipedia
Rozeta z kościoła St-Jean-de-Malte w Aix-en-Provence
Rozety
Jednym z najbardziej charakterystycznych elementów architektury średniowiecznej, zwłaszcza gotyckiej, są rozety. Są to okrągłe okna z delikatną konstrukcją kamienną, których puste przestrzenie są najczęściej wypełnione witrażami. Pierwsze rozety pojawiają się już w kościołach romańskich; zamiast witrażami są wypełnione cienkimi płytkami kamiennymi, przepuszczającymi światło.
-
Połowa równoległoboku
-
Gra Grim i twierdzenie Sprague’a–Grundy’ego
Pewnie część czytelników Delty zna grę Nim – zarówno jej zasady, jak i właściwą dla niej strategię wygrywającą. W tym artykule chcemy przedstawić inną grę grafową. Grę o prostych zasadach, ale trudniejszą niż Nim do dokładnego przeanalizowania. Tą grą jest – stworzony przez Jamie Peabody i Karen Willis – Grim. Podamy efektywny sposób orzekania, który gracz ma strategię wygrywającą. Co najciekawsze, można go zastosować do szerokiej klasy tego typu gier dwuosobowych, zawierającej Grima i Nima.
-
Rekordy długowieczności i procesy Poissona II
W pierwszej części artykułu szukaliśmy prawdopodobieństwa tego, że umierający człowiek będzie starszy od wszystkich aktualnie żyjących. Zadanie wykonaliśmy. Obliczyliśmy interesujące nas prawdopodobieństwo. Pozwólmy sobie teraz na kilka komentarzy i dygresji. Przypomnijmy najważniejszy wynik pomocniczy, który udowodniliśmy przed miesiącem.
-
Szczęście w zbiorach mierzalnych
Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.
-
Jaki jest następny wyraz tego ciągu?
3, 7, 31, 211, 2311, ... – jaki jest następny wyraz tego ciągu? Jakiś czas temu taka zagadka pojawiła się na jednej z polskich rozrywkowych stron internetowych. Niemal od razu w komentarzach pod nią rozpoczął się spór o poprawne, prawdziwe rozwiązanie. Czytelnik zapewne zechce podjąć wyzwanie samodzielnego odnalezienia następnego elementu ciągu i jego ogólnej reguły. Zatem zatrzymajmy się tu i pozwólmy sobie na chwilę namysłu; w dalszej części tekstu pojawi się rozwiązanie (autorowi niniejszego tekstu zajęło kilka dłuższych chwil znalezienie formuły).
-
Kto by się spodziewał
Kto by się spodziewał, że prawdziwe jest stwierdzenie: jeśli w sześcianie mieszczą się trzy jednakowe kulki, to zmieści się też czwarta tej samej wielkości!
-
Piłka w puszce
Piłki tenisowe na ogół pakowane są w rurkę po kilka sztuk. Wyobraźmy sobie piłki tak cenne, że pakowane są każda oddzielnie. Takie opakowanie to z matematycznego punktu widzenia walec...
-
Bardzo oszczędne drzewa (II)
Skoro dotychczas szło nam tak dobrze, spróbujmy pójść za ciosem i zaproponować bardzo oszczędną reprezentację drzew już niekoniecznie binarnych (ale wciąż ukorzenionych)...
-
Kraina dwóch monet
Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 5 i 9. Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty...
-
Kosmiczne jaja
Ruch obiegowy Ziemi wokół Słońca przy stałym kierunku osi obrotu planety i nachyleniu do płaszczyzny orbity sprawia, że w ziemskiej pogodzie pojawiają się cyklicznie pory roku. Obecnie promienie słoneczne padają na północną półkulę pod coraz większym kątem, średnia temperatura rośnie, dzień staje się dłuższy, a noc krótsza, co naturalnie skłania do rozważań o odchodzącej zimie i odradzającym się z nadchodzącą wiosną życiu. Zadziwiające, że jednym z wykorzystywanych przez praktycznie wszystkie kultury symbolem wiosny i nowego życia jest jajo...
-
Rekordy długowieczności i procesy Poissona
-
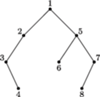
Rys. 1
Bardzo oszczędne drzewa (I)
Wiele struktur danych w komputerze można reprezentować w postaci drzewa binarnego. Aby przechować takie drzewo w pamięci komputera, należy dla każdego węzła zapamiętać numer jego lewego i prawego syna oraz, jeśli to potrzebne, numer węzła będącego jego ojcem. Wystarczą nam do tego trzy tablice.
-
Człapanie do nieskończoności
Matematyka, jak przystało na królową nauk, jest dyscypliną dość trudną i wymagającą umiejętności abstrakcyjnego myślenia. Jeżeli przyjąć za Galileuszem, że matematyka jest alfabetem, za pomocą którego Bóg opisał wszechświat, to trzeba przyznać, że jest to alfabet dość złożony i nie jest łatwo nauczyć się dobrze nim posługiwać. Jednym z jego ważniejszych elementów jest niewątpliwie nieskończoność.
-
Heron uogólniony?
Wzór Herona
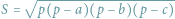 pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
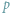 to połowa obwodu).
Czy da się go uogólnić, na przykład dla objętości czworościanu lub pola
czworokąta?
to połowa obwodu).
Czy da się go uogólnić, na przykład dla objętości czworościanu lub pola
czworokąta?
-
Postaw na krawędzi!
Postawmy czworościan na krawędzi i przez każdą jego krawędź poprowadźmy płaszczyznę równoległą do przeciwległej krawędzi. Takich sześć płaszczyzn wyznacza równoległościan opisany na czworościanie.
-
Samą linijką można nakreślić okrąg...
...jeśli ma się 5 jego punktów. No, może trochę przesadziłem... Okręgu tak dosłownie nakreślić nie można, ale można narysować jego kolejnych kilka punktów, nawet gdy te kilka to np. 100 -- oczywiście, im większa będzie to liczba, tym dłużej będzie to trwało, bo rysować będziemy te punkty kolejno, po jednym.
-
Istnienie
Gdy chcemy coś badać, rozsądnie jest upewnić się, że to coś istnieje...