Elementarnie o twierdzeniu Brouwera
Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej 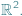 Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
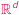


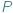 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 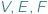 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 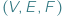 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości: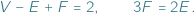


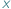 i
i 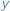 mamy
mamy 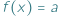 i
i 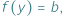 to w przedziale
to w przedziale 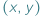 są przyjmowane wszystkie wartości między
są przyjmowane wszystkie wartości między  i
i 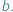 Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...