Delta mi!

Podczas odbywającego się w 1900 roku w Paryżu Drugiego Międzynarodowego Kongresu Matematyków jeden z referatów wygłosił wybitny niemiecki matematyk David Hilbert. W swoim wystąpieniu zawarł on listę dwudziestu trzech zagadnień matematycznych stanowiących, jego zdaniem, szczególne wyzwanie dla matematyków w rozpoczynającym się XX wieku. Większość z nich doczekała się rozwiązania. Inne, jak słynna hipoteza Riemanna, pozostają otwarte, inspirując kolejne pokolenia naukowców.

Czy lubicie długoterminowe prognozy pogody? Odbija się w nich głęboko zakorzeniona ludzka wiara, że odległą przyszłość można przewidzieć - na przekór efektowi motyla. No cóż, sam muszę przyznać, że cieszę się, gdy grudniowe prognozy przewidują piękną, słoneczną i mroźną aurę na zimowe ferie; ale jeśli zapowiadają ponury mokry standard, wtedy ratuję się myślą, że to przecież tylko prognoza...

Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.

Nagraliśmy ze znajomymi piosenkę. Nie było to profesjonalne przedsięwzięcie: nie wynajęliśmy studia nagraniowego, ale spotkaliśmy się u jednego z nas, wyjęliśmy instrumenty i zagraliśmy kilka razy do porządnego dyktafonu. Niestety, brak zawodowstwa dało się odczuć natychmiast - okazało się, że siedziałem na skrzypiącym krześle, które przy każdym moim ruchu robiło ziiik, ziiiiiik. Skrzypienie, choć nie permanentne, stanowczo utrudniało percepcję.

Teoria liczb to prawdopodobnie najstarsza dziedzina wiedzy matematycznej, badana intensywnie już w czasach starożytnych (a zapewne jeszcze wcześniej; możliwe, że nawet zanim powstała jakakolwiek cywilizacja operująca przekazem pisemnym).

W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.

O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.

W tym odcinku zajmiemy się hipotezą continuum.

Pokazy iluzjonistyczne nacechowane są elementami odwracającymi uwagę, nadzwyczajną zwinnością, sprawnością ruchową lub rachunkową iluzjonisty. Dla nas, matematyków, najciekawsze są oczywiście te wykorzystujące pewne aspekty matematyki. Przedstawimy kilka trików, które łączy wspólne ogniwo - systemy pozycyjne.

Tym razem o kilku ciekawych własnościach funkcji Eulera.

Niech autorowi będzie wolno cofnąć się w czasy lśniących w słońcu chromowanych obręczy kół rowerów (lub wózków dziecinnych). Obręcze te rzucały rozmaite odblaski na powierzchnię szosy. Bogactwo obserwowanych kształtów zachęcało do podjęcia próby opisania ich w języku matematyki. Zróbmy to teraz, choć poniewczasie - bo współcześnie trudniej o okazję ujrzenia tego zjawiska.

Gdy w zadaniu występuje kąt o mierze będącej wielokrotnością to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.

W pierwszej połowie XX wieku znaczący postęp prac nad matematycznymi modelami zjawisk losowych doprowadził do powstania wyodrębnionego działu matematyki wykorzystującego zaawansowane metody algebry i analizy matematycznej. Tematów badawczych dostarczały pytania stawiane przez specjalistów różnych dziedzin. Abstrahowanie od szczegółowych cech badanych zjawisk w procesie modelowania matematycznego niejednokrotnie prowadziło do zbliżonych opisów różnych zagadnień. Dzisiaj mówimy o zastosowaniach rachunku prawdopodobieństwa, które posiłkują się teorią procesów stochastycznych i statystyką. Jednolity model matematyczny stawał się także narzędziem do wykorzystania przy badaniu zagadnień, do analizy których nie wykorzystywano wcześniej metod matematycznych...

Tytuł niniejszego artykułu jest zestawieniem dwóch pozornie odległych pojęć matematycznych. Pierwszym z nich jest trójkąt Sierpińskiego - jeden z najlepiej rozpoznawalnych fraktali. Drugim jest gra w życie - automat komórkowy opisany w 1970 roku przez Johna Conwaya.

Modelowanie matematyczne jest pewnego rodzaju sztuką opisywania świata - zarówno w skali mikro, jak i makro - za pomocą równań matematycznych (równań różniczkowych, różnicowych czy stochastycznych). Opis mikroskopowy może dotyczyć zachowania pojedynczych molekuł (cząsteczek), natomiast obiektem opisu makroskopowego jest to, co widzimy "gołym okiem", m.in. przemiany zachodzące w wyniku reakcji chemicznych. Mogą to być zmiany właściwości fizycznych danych substancji (np. stan skupienia, barwa, gęstość) lub chemicznych (np. zapach, smak, toksyczność)...

W salonie fryzjerskim siedzi matematyk, obok leży połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Matematyk nerwowo wierci się w fotelu - przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł - warkocz będzie idealny!

W poprzedniej części tej opowieści o nieskończonościach rozważaliśmy twierdzenie Cantora, które stanowi, że żaden zbiór nie jest równoliczny ze zbiorem jego podzbiorów 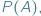co symbolicznie notujemy 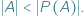Szczególnie zajmowaliśmy się przypadkiem, gdy 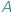jest zbiorem liczb naturalnych

Każdy widział kiedyś bańki mydlane. Nie ma co ukrywać, są one okrągłe. Tylko dlaczego?

W poprzednim odcinku naszej sagi przedstawiliśmy miłosną historię Aldony i Bogumiła. Poniżej prezentujemy jej dość dramatyczną kontynuację, widzianą oczami Aldony...