Czwarty wymiar – zobaczmy
Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.
Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.
Uczciwi złodzieje powinni umieć się dzielić. Oczywiście, dzielić się łupami z innymi uczciwymi złodziejami, którzy pomagali w dokonaniu kradzieży. Można sobie wyobrazić, że taka uczciwość powoduje czasem pewne trudności, gdyż niektóre precjoza mogą być nieskore do podziału. Dla przykładu...
Problem szyfrowania przesyłanych wiadomości sięga jeszcze czasów starożytnych, więc naszego nowego deltowego cyklu artykułów o kryptologii prezentowanego w rubryce "A jednak się da!" nie możemy nie zacząć od przypomnienia najstarszego znanego systemu szyfrowania, mianowicie szyfru Cezara. Szyfr ten nie jest specjalnie wyrafinowany...

Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
Zupełnie nieszokująca zasada dobrego uporządkowania mówi, że każdy niepusty podzbiór liczb naturalnych ma element najmniejszy. Pokażemy, jak ją wykorzystać do wykazania, że 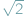 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 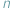 liczba
liczba 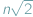 nie jest całkowita.
nie jest całkowita.
Jaka jest liczba różnych 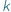 -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 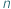 -elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez
-elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez 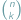 (symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
(symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
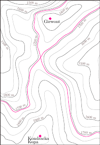
Typowe (regularne) poziomice zaznaczone są na szaro, a nietypowe (osobliwe) na kolorowo.
Mapa obok przedstawia rejon Giewontu i Kopy Kondrackiej. Typowa poziomica jest albo pusta (np. nie ma żadnych punktów na wysokości 2500 m), albo składa się z jednej lub więcej składowych, z których każda jest albo zamkniętą pętlą (jak ta wokół Giewontu, 1800 m), albo krzywą o dwóch końcach na brzegu mapy (np. te powyżej dolin Małej Łąki i Kondratowej, 1600 m). Może się jednak zdarzyć, że poziomica jest osobliwa - na wysokości 1894 m mamy izolowany punkt (szczyt Giewontu), a na 1725 m przecięcie w kształcie litery X (Kondracka Przełęcz). Są to jednak pojedyncze przypadki - jak szczyt, przełęcz albo dno kotła - a wszystkie pozostałe poziomice są regularne.

Chaim Zelig Słonimski (1810-1904)
Przy dzieleniu liczb wielocyfrowych metodą pisemną często wykonuje się następującą operację...
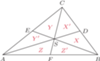
Punkty D, E, F to środki boków, X, X', Y, Y', Z, Z' oznaczają pola.
Środkowa trójkąta to odcinek łączący wierzchołek ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości i dzieli on każdą z nich w stosunku 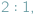 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).
Sztuczna inteligencja Nowe pomysły
W 1970 roku jeden z pionierów sztucznej inteligencji, Marvin Minsky, napisał na łamach Life Magazine, że w ciągu 8 lat pojawią się maszyny o inteligencji porównywalnej z ludzką lub ją przewyższające. Jednak takie maszyny nie pojawiły się ani do roku 1978, ani przez kolejne 40 lat. A jednak w ciągu ostatnich lat można zobaczyć znaczne przyspieszenie w dziedzinie sztucznej inteligencji: autonomiczne samochody, programy wygrywające z ludzkimi arcymistrzami w Go - ostatnią grę, w którą człowiek dotychczas był lepszy, czy roboty humanoidalne śmiało przemierzające gruzowiska. Być może prognoza Minskiego, choć znacznie opóźniona, ziści się na naszych oczach?
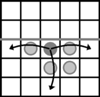
Rys. 1 Możliwe ruchy ciemnoszarego pionka
Conway's Soldiers to jednoosobowa łamigłówka, w której żołnierze (pionki) przedostają się na terytorium wroga i chcą wkroczyć jak najdalej. Na nieskończonej szachownicy, z zaznaczoną "na środku" poziomą granicą, pionki przeskakują jeden nad drugim. Dokładniej: ruch polega na przeskoczeniu pionkiem nad innym znajdującym się na sąsiadującym polu - tylko poziomo lub pionowo - i zdjęciu pionka, który został przeskoczony.
Tak zwana "kryptografia krzywych eliptycznych" to bardzo modne i popularne pojęcie, które rzeczywiście jest ważne, ale - niestety - o którym mówi się najczęściej niezwykle powierzchownie, bez wchodzenia w "detale matematyczne". Niniejszy artykuł próbuje pójść takiemu podejściu pod prąd - chcemy w elementarny sposób objaśnić, o co tak naprawdę chodzi z tymi krzywymi eliptycznymi.
Zagadnienia związane z prawdopodobieństwem i statystyką bywają zaskakujące i nieintuicyjne. Zdarza się też często, że okazują się one znacznie łatwiejsze niż się na pierwszy rzut oka wydaje.
Zacznijmy od następującego zadania: dwunastu Indian (dla ustalenia uwagi i zgrabności tytułu przyjmijmy, że pochodzą oni z plemienia Mohikanów) siedzi dookoła ogniska i pali fajkę pokoju. Procedura rozpoczyna się rzecz jasna od Wodza, który po zapaleniu rzuca zdobytą od bladych twarzy symetryczną monetą i w zależności od wyniku podaje fajkę na lewo albo na prawo. Kolejny Indianin robi to samo - pali faję, rzuca monetą i podaje dalej (fajkę, nie monetę). Nietrudno uwierzyć, że prędzej czy później fajka wpadnie w ręce ostatniego Indianina, który jej wcześniej nie palił (będzie to tytułowy ostatni Mohikanin)...
Praca nadesłana na Konkurs Prac Uczniowskich dotyczy nowej metody dowodzenia pewnych nierówności. W niniejszym skrócie umieszczam jedynie ważniejsze twierdzenia (bez dowodów) i niektóre ich zastosowania.
Nierówności między średnimi, a w szczególności nierówność między średnią arytmetyczną i geometryczną (oznaczana dalej A-G), to jedne z podstawowych narzędzi dowodowych w arsenale każdego olimpijczyka...
Pierwszy etap pitagoreizmu głosił hasło wszystko jest liczbą: pożądaną Harmonię Świata da się wyrazić jako stosunek liczb (dziś nazywanych naturalnymi), przy czym jest ona tym pełniejsza, im liczby te są mniejsze.
W roku 1970 Martin Gardner opisał w dziale matematycznym czasopisma Scientific American kostki do gry odkryte kilka lat wcześniej przez statystyka Bradleya Efrona...
Tym razem o paraboli...