Delta mi!

Tematem poprzedniego deltoidu była inwersja na płaszczyźnie. Analogicznie przekształcenie zdefiniować można w przestrzeni...

W tym kąciku chcielibyśmy powrócić do pewnych własności sfery wpisanej w czworościan, o których pisaliśmy w kąciku 2 o najmocniejszym twierdzeniu stereometrii (Delta 3/2010). Okazuje się, że można je wykorzystać do udowodnienia faktów pozornie niezwiązanych ze sferą wpisaną.

Słowa, którymi będziemy się zajmowali, będą napisami złożonymi z liter jednego lub kilku zbiorów (na początek przyjmijmy, że zbiory są dwa – jeden zawiera małe litery łacińskie, a drugi duże) o tej własności, że dwie jednakowe litery umieszczone po kolei będą znikały. Napis, w którym wszystko znikło (czasem i taki jest potrzebny), będzie oznaczany 1.

Na zawodach II stopnia VIII OMG, które odbyły się 5 stycznia 2013, jedno z zadań było następujące...

Dwunastościan rombowy jest figurą o zadziwiających własnościach. Narysowanie go nie powinno sprawiać większych trudności. Jak nazwa wskazuje, ścianami tego dwunastościanu są romby, zatem rysunek zaczynamy od narysowania właśnie rombu.

Gra Mastermind jest rozrywką głównie dla gracza odgadującego. Przypomnijmy: musi on ustalić, jaki kod (ciąg czterech kolorowych szpilek) ułożył przeciwnik, posiłkując się odpowiedziami otrzymywanymi na zadawane pytania. Pytania muszą mieć postać „Jak bardzo kod przypomina ciąg X?”, zaś odpowiedzią są dwie liczby: trafień właściwych kolorów na właściwych pozycjach oraz trafień kolorów na pozycjach niewłaściwych (odpowiednio: trafienia celne i niecelne; te pierwsze będziemy też nazywać po prostu trafieniami). Oczywiście chodzi o to, by odgadnąć kod jak najszybciej.

Tym razem o inwersji – przekształceniu określanym czasem jako symetria względem okręgu.

Tym razem opowiemy o punkcie Fermata–Torricellego w czworościanie...

W Delcie 6/2011 artykuł Marii Donten-Bury o płaszczyźnie rzutowej został poprzedzony przedstawieniem sześciu jej (płaszczyzny, nie Marysi) postaci, pod jakimi daje się nam ona zaobserwować. Wobec tego, że postacie te są bardzo różnorodne, nasunąć się może wątpliwość, czy faktycznie wszystkie są wcieleniami tego samego matematycznego obiektu. Poniżej jest przedstawiony sposób, jak tę wątpliwość można rozstrzygnąć.

30 maja 1832 roku w Paryżu zginął w pojedynku młody matematyk, Evariste Galois. Nie ma pewności, czy pojedynek ten miał podłoże polityczne, czy też Galois bronił honoru pewnej młodej damy. W pożegnalnym liście poprosił on, by jego notatki wysłać Jacobiemu albo Gaussowi. Żaden z tych wielkich matematyków nigdy nie zobaczył jednak zapisków Galois.

Ostatnio rysowaliśmy dwunastościan foremny i dwudziestościan foremny. Przedstawimy jeszcze jeden sposób rysowania dwunastościanu foremnego.

Rozważmy następujący problem, zwany problemem kapeluszy (ang. hat problem). Do pokoju wchodzi  osób i każdej z nich losowo zostaje nałożony niebieski lub czerwony kapelusz. Każdy widzi kapelusze pozostałych osób, ale nie widzi swojego. Żadna komunikacja nie jest dozwolona, z wyjątkiem ustalenia strategii przed rozpoczęciem gry...

Dla trójkąta definiujemy okrąg opisany i okrąg wpisany. Podobnie z czworościanem można związać dwie naturalne sfery: sferę przechodzącą przez wierzchołki (opisaną) oraz sferę styczną do ścian (wpisaną). Można jednak rozważać jeszcze trzecią ciekawą sferę – styczną do krawędzi.

Rozwiązywanie równań diofantycznych jest jednym z ważniejszych problemów klasycznej teorii liczb. Czytelnicy tego artykułu na pewno słyszeli o równaniu Pella 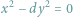 czy równaniu Fermata

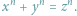
Nie od dziś wiadomo, jak zbudować najprostszy zegar słoneczny. Słońce, w swym pozornym ruchu po niebie, porusza się ze stałą prędkością kątową w płaszczyźnie prostopadłej do osi wskazującej północny biegun niebieski...

W podróży bardzo istotną rolę odgrywa mapa, na której określa się i zaznacza aktualną pozycję, rozmaite odległości (np. odległość przebytą, do mijanych obiektów, pozostałą do celu podróży) oraz kąty (np. kursy, namiary).

W dowodzeniu nierówności często pomocna bywa tak zwana metoda stycznych. Zdarza się, że wykres funkcji leży nad pewną prostą styczną do niego lub pod taką prostą (wszędzie lub tylko na jakimś przedziale). To oznacza, że możemy oszacować wartości tej funkcji przez wartości funkcji liniowej, której wykresem jest wybrana styczna. Żeby takie oszacowanie doprowadziło do celu, wybrana styczna musi przechodzić przez punkt, dla którego badana nierówność jest równością. Przyjrzymy się kilku przykładom zastosowań tej metody.

Narysujemy teraz figurę bardziej skomplikowaną: dwudziestościan...

W dzisiejszym świecie ludzie stają się coraz bardziej leniwi. Chcą osiągnąć zysk w krótkim czasie, bez zbytecznej pracy. Najłatwiejszym sposobem na „zarabianie” są gry. Ale czym właściwie jest gra?