Delta mi!

Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.

Niektóre gry mogą wydawać się trudne, dopóki gracz się nie dowie, o co tak naprawdę w nich chodzi – wtedy nagle te same gry okazują się łatwe, czasem wręcz oczywiste...

Chyba wszyscy lubimy liczby pierwsze. Szczególne wrażenie robią te naprawdę duże, wydają się skrywać w sobie jakąś nadzwyczajną tajemnicę: dlaczego akurat one stały się swego rodzaju wybrańcami spośród innych liczb i mają tak niezwykłe właściwości?

Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.

W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.

Przemieszczając się na płaszczyźnie za pomocą ruchów „do przodu”, „do tyłu”, „w lewo” i „w prawo”, możemy w szczególności narysować kwadrat. Czy analogiczna sytuacja rozważana na zakrzywionej powierzchni zawsze pozwala na wygenerowanie kwadratu przez zakreślaną trajektorię? Rozważmy sferę, którą często wykorzystuje się w globalnym modelowaniu powierzchni Ziemi.

W fizyce szkolnej nieustannie przewijającym się motywem są dwa znane miasta: miasto A oraz miasto B. W kryptografii takimi gwiazdami są Alicja i Bob, którzy ciągle się komunikują, uwierzytelniają, a zwykle przeszkadza im w tym złowroga Ewa.

Sprawdź, Czytelniku, czy potrafisz...

Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.

7 stycznia 2012 roku około 1400 uczniów wzięło udział w drugim etapie VI Olimpiady Matematycznej Gimnazjalistów. Najciekawszym i jednocześnie najtrudniejszym zadaniem okazało się zadanie z planimetrii oznaczone numerem 5. Rozwiązało je niewielu uczniów, przy czym żaden z nich nie rozważył wszystkich możliwych konfiguracji. Poniżej postaramy się zadanie to dokładnie zanalizować.

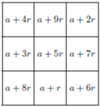
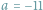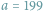Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny obok kwadrat magiczny jest dla  (lub ) i 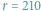  złożony z samych liczb pierwszych.

W Delcie 3/1979 zamieściliśmy największy znany wówczas kwadrat magiczny złożony z różnych liczb pierwszych – było ich 169. Co więcej, był to kwadrat „cebulkowy”. A dziś – proszę: istnieje już „cebulkowy” kwadrat magiczny aż o trzy większy, złożony zatem z dwustu pięćdziesięciu sześciu liczb pierwszych. I jak tu nie wierzyć w postęp!

Czy istnieje czworościan który nie jest foremny, a którego ściany są trójkątami przystającymi? Istnieje...

Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...

Sophie Germain (1776–1831), wbrew ówczesnym obyczajom matematyk, fizyk, metalurg i autorka ciekawych szkiców o kulturze, prawie na każdym kroku musiała udowadniać swą wiedzę i bronić swych dokonań przed rzeszami niedowiarków.

Twierdzenie o jednoznaczności rozkładu na czynniki pierwsze w zbiorze liczb naturalnych wypowiada się najprościej w następujący sposób: każdą liczbę naturalną różną od jedności możemy przedstawić w postaci iloczynu 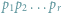 liczb pierwszych na jeden tylko sposób, o ile rozkłady, różniące się kolejnością czynników, uważać będziemy za równe...

Co to jest liczba pierwsza? Najkrótsza definicja mówi, że to taka liczba naturalna, która ma dokładnie dwa dzielniki. Każda liczba naturalna ma przynajmniej dwa dzielniki: 1 i samą siebie. Wyjątkiem jest jedynka, dla której te dwa dzielniki okazują się tym samym.

Jednym z fundamentalnych pojęć analizy matematycznej jest bez wątpienia różniczkowalność. Dla funkcji jednej zmiennej, określonej na pewnym otwartym przedziale, równoważna jest ona istnieniu pochodnej funkcji w każdym punkcie tego przedziału. Jak wiadomo, wszystkie funkcje elementarne są różniczkowalne w tym klasycznym sensie, jednak wiele innych prostych i zarazem użytecznych funkcji już nie.