-
-

Środek przeciwprostokątnej
Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.
-

Co ma wspólnego bryła Wulffa z płatkami śniegu?
Drogi Czytelniku, jeśli popatrzysz na płatki śniegu, to zobaczysz wielką ich rozmaitość. Bogactwo znanych kolekcji zdjęć śnieżynek mówi nam, że nie ma dwóch identycznych płatków śniegu. Możesz zapytać, czy możemy skatalogować pokrój kryształków lodu i wyjaśnić ich kształt?
-

W co grają kraje, eksploatując środowisko?
4 września 1958 roku islandzki statek patrolowy ICGV Ægir próbował zatrzymać brytyjski kuter rybacki poławiający w strefie 12 mil morskich od brzegów Islandii, został jednak staranowany przez brytyjski okręt wojenny HMS Russell. To był pierwszy incydent pierwszej wojny dorszowej. Co było przyczyną serii konfliktów, w których przeciwko jednej z największych marynarek wojennych Europy stanęła licząca siedem okrętów patrolowych i jeden wodolot flota Islandii? Czego broniła tak zaciekle?
-

wikipedia
Dictostelium discoideum
Równania chemotaksji i wybuchy rozwiązań
Patrząc z bardzo ogólnego punktu widzenia, całą obserwowalną przyrodę ożywioną i nieożywioną można przedstawić jako wzajemnie powiązane procesy, czyli funkcje, które chwilom przyporządkowują stany różnych obiektów wyrażone poprzez wartości liczbowe. Aby przewidywać przebieg rożnych procesów, tworzy się modele matematyczne, które określają w każdej chwili zmiany stanów procesów w zależności od samych stanów. Matematycznie zmianę funkcji opisuje jej pochodna (różniczka), która określa, jak wielkie są przyrosty ewentualnie spadki wartości funkcji w krótkich przedziałach czasu. Równania, których rozwiązaniami są owe procesy przyjmujące jakieś zadane stany początkowe, to równania różniczkowe zwyczajne...
-
O rybach i ufności
W poprzednim numerze Delty przedstawiliśmy zgrabną metodę szacowania liczby ryb pływających w stawie. Przypomnijmy doświadczenie, na którym ta metoda się opierała: najpierw łowimy rybkę, potem rysujemy jej kreskę na ogonku, następnie na kartce zapisujemy liczbę kresek, jakie widzimy na ogonku trzymanej w ręce rybki, po czym wrzucamy ją z powrotem do stawu i całą procedurę powtarzamy
 razy.
razy. -
Porządek w stochastycznym świecie
Rozważymy dwie uporządkowane struktury, które są wynikiem optymalizacji pewnych deterministycznych wielkości: minimalizacji energii w stanach podstawowych oddziałujących cząstek oraz maksymalizacji wypłat w równowagach Nasha rywalizujących graczy. Zadajemy pytanie - czy porządek obecny w powyższych strukturach przetrwa stochastyczne zaburzenia zawsze obecne w rzeczywistych układach?
-

industry.it4i.cz
Zastosowania matematyki Co to jest?
30 lat addytywnej metody Schwarza
Gotów jestem założyć się, Czytelniku, że wcześniej o niej nie słyszałeś. Tymczasem pod tą mało medialną nazwą kryje się metoda, dzięki której współczesne superkomputery pracują pełną parą, prowadząc skomplikowane symulacje. Łączy ona w sobie algorytmiczną efektywność z fizyczną intuicją, a bez wglądu w jej matematyczny sens, być może, nigdy byśmy jej nie poznali.
-
O zastosowaniach Combinatorial Nullstellensatz
Zadanie 6 z 48. Międzynarodowej Olimpiady Matematycznej (IMO) z 2007 roku było jednym z najtrudniejszych w historii Międzynarodowej Olimpiady Matematycznej.
-
Jak zwalczać losowość w grach
Losowość w grach karcianych, planszowych i komputerowych często budzi wiele kontrowersji. Sprawia ona, że gracz słabszy grający z lepszym ma szansę wygrać. Jest to pożądane w przypadku gier towarzyskich i frustrujące w przypadku gier profesjonalnych. W obu przypadkach nadmiar losowości jest zły, gdy za często zdarza się, że przewaga gracza pierwszego, wynikająca z jego inteligentnej gry, jest niwelowana przez szczęście drugiego. W moim artykule pokażę, jak z losowością można walczyć na przykładzie jednej z najbardziej losowych gier, czyli Chińczyka, którego, mam nadzieję, wszyscy znają.
-
Jedno zdanie
O trudnym problemie, który ma jednozdaniowe rozwiązanie...
-
Najpiękniejsze zadanie geometryczne
Znam takie zadanie. Jego autorem jest Igor Fiodorowicz Szarygin. Jego treść jest nieskomplikowana: jak szeroki walec można włożyć pomiędzy trzy jednakowe, parami prostopadłe walce?
-
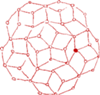
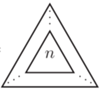
Liczenie ryb w jeziorze metodą statystyczną i śliczną, choć probabilistyczną
W jeziorze pływa
 ryb, ale liczby
ryb, ale liczby  nie znamy. Chcielibyśmy tę liczbę oszacować, nie uciekając się do osuszenia jeziora. Powiedzmy, że dysponujemy wędką, puszką farby i odrobiną wiedzy ze statystyki. Łowimy sobie jedną rybkę po drugiej i wrzucamy z powrotem do jeziora, krzywdy żadnej rybce nie czyniąc. Przed wrzuceniem do wody malujemy rybce kreseczkę na ogonku...
nie znamy. Chcielibyśmy tę liczbę oszacować, nie uciekając się do osuszenia jeziora. Powiedzmy, że dysponujemy wędką, puszką farby i odrobiną wiedzy ze statystyki. Łowimy sobie jedną rybkę po drugiej i wrzucamy z powrotem do jeziora, krzywdy żadnej rybce nie czyniąc. Przed wrzuceniem do wody malujemy rybce kreseczkę na ogonku... -
Warto (się) rozwijać
Jeśli chcemy wyznaczyć długość pewnej krzywej lub łamanej, często warto ją rozwinąć albo w inny sposób rozprostować.
-
Obsesja dużych liczb
Kiedy miałem kilka, kilkanaście lat, wraz ze starszym bratem często graliśmy w grę. Należało w swojej kolejce podać liczbę większą od wskazanej przez poprzednika. Przegrywał oczywiście ten, kto nie był w stanie podać liczby większej. Czasami ponosiła nas fantazja i mówiliśmy "nieskończoność" albo "nieskończoność plus nieskończoność". Dziś już wiem, że nieskończoność liczbą nie jest, a działania na nieskończonościach są bardziej wyrafinowane, niż podejrzewałem. Gdyby i Tobie, drogi Czytelniku, przyszło kiedyś wymienić (albo usłyszeć) jakąś dużą liczbę, możesz sięgnąć do poniższej listy. Nie są to bowiem byle jakie liczby...
-
Rachunek prawdopodobieństwa Mała Delta
Stawka większa niż...?
Historyjka na marginesie poniżej przedstawia tzw. problem podziału stawki - jedno z zadań, jakimi żywił się raczkujący rachunek prawdopodobieństwa u początków swojego istnienia. W źródłach europejskich pojawia się on po raz pierwszy w podręczniku Summa de Arithmetica, Geometrica, Proportioni, et Proportionalita włoskiego franciszkanina, Luki Paccioliego (1445-1517).
-
Liczby pierwsze jako niewiadome
W historii ludzkiego poznania mało jest tak fascynujących pojęć jak liczby pierwsze. Chociaż dzisiaj wiemy o nich znacznie więcej niż 120 lat temu, to jeszcze więcej dotyczących ich pytań pozostaje bez odpowiedzi. Celem tej notki jest pokazanie, że trudno jest ocenić na pierwszy rzut oka, czy pytanie dotyczące liczb pierwszych jest łatwe, czy też bardzo trudne - poza zasięgiem współczesnej nauki.
-
Z samą linijką na okrąg
Dany jest okrąg...
-
Zadanie Alhazena
Gdy na lustrzaną sferę pada promień światła, odbija się on tak, że kąt między nim a przedłużeniem promienia sfery przechodzącego przez punkt, w którym promień pada, jest równy kątowi między tym przedłużeniem a promieniem odbitym, przy czym wszystko odbywa się w jednej płaszczyźnie wyznaczonej przez padający promień i środek sfery. Geometrycznie sytuacja jest więc dwuwymiarowa.
-
Wielościan w zeszycie
Prawie każdy wielościan ma talię (to wśród nich jest nawet częstsze niż u ludzi!), czyli pewien jego płaski przekrój ma obwód mniejszy od sąsiednich (dokładniej: niewielka zmiana płaszczyzny tnącej daje wielokąt o większym obwodzie - a bardziej po ludzku: nałożona w takim miejscu gumka recepturka nie zsunie się). Dla sześcianu taką talią jest jego przekrój będący sześciokątem foremnym (narysuj ją!).