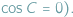Kluska w uchu wielbłąda albo arytmetyka moralna
Powiada Ewangelia: Łatwiej jest wielbłądowi przejść przez ucho igielne, niż bogatemu wejść do królestwa niebieskiego.
Powiada Ewangelia: Łatwiej jest wielbłądowi przejść przez ucho igielne, niż bogatemu wejść do królestwa niebieskiego.
Na stole leżą, ułożone w losowej kolejności koszulkami do góry, trzy karty: As, Król i Dama. Jeżeli gracz odgadnie prawidłowo położenie Asa, wygrywa dużą nagrodę. Gracz wskazał kartę, nie obejrzał jej, i wtedy prowadzący grę mówi: Chwileczkę. Odkryję jedną z dwóch pozostałych kart, a ty się zastanów, czy chcesz zmienić swoją kartę na kartę, która pozostała nieodkryta.
Chyba każdy patrzył kiedyś w kalejdoskop - prostokątne lustra odbijające różnobarwne wzory powstałe z przesypujących się koralików. Nie znam nikogo, kto mając w ręku owo urządzenie, byłby w stanie powstrzymać się przed choćby najmniejszym obróceniem nim i zerknięciem przez małe oczko na otrzymany efekt. A gdyby odwrócić sytuację i zbadać, jak zmieni się obraz, gdy zamiast koralikami poruszymy lustrami znajdującymi się w kalejdoskopie? Zacznijmy od wyprawy do szklarza i wyboru bohatera kalejdoskopowych przygód - po starannym castingu wygrywa żaba.
W swojej pracy astronomowie często korzystają z katalogów będących wynikiem wielkich przeglądów nieba. Zebrane w nich dane poddawane są różnorakim analizom. Ważne jest przy tym, aby katalogi charakteryzowały się jak największą kompletnością i jednorodnością. Niejednokrotnie podczas analizy statystycznej dobrze poznanych typów obiektów wykrywane są źródła rzadko spotykane lub wykazujące niezwykłe zachowanie. Dlatego też odpowiedni sposób klasyfikacji obserwowanych obiektów jest bardzo istotnym, o ile nie najistotniejszym krokiem, który należy wykonać przed przystąpieniem do zaawansowanego badania właściwości fizycznych obserwowanych obiektów niebieskich.
Gry, zagadki, paradoksy Mała Delta
Rzucamy monetą. Jeśli wypadnie orzeł - wygrywam ja, jeśli reszka - wygrywa mój przeciwnik. Czy jest to gra sprawiedliwa? Uważam, że tak. A oto inna gra. Rzucamy kostką do gry. Jeśli wypadnie szóstka - wygrywa mój przeciwnik, jeśli co innego - wygrywam ja. W moim odczuciu ta gra jest niesprawiedliwa, niekorzystna dla mojego przeciwnika. Czy zgadzacie się ze mną? Jeśli tak, to w porządku, rozumiemy się doskonale...
Stereometria Nowości z przeszłości
W 1752 roku znakomity matematyk szwajcarski Euler, podówczas profesor Akademii Nauk w Berlinie, odkrył zadziwiający związek między liczbami 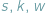 ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego
ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 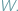 Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci

Podamy elementarny i chyba nader zabawny dowód tego wzoru.

W matematycznym świecie od zawsze znajdowało się mnóstwo tajemnic czekających na odkrycie. Tak zawiłych i zdradzieckich, że tylko szaleńcy mogli w ogóle wyobrazić sobie ich istnienie. Tymi szaleńcami byli nieustraszeni matematycy, którzy już od stuleci (jeżeli nie tysiącleci) szukają, rozwiązują i wyjaśniają zagadki, które większość ludzi już dawno uznawała za beznadziejne przypadki (lub są one tak abstrakcyjne, że w żaden sposób nieosiągalne).
Rachunek prawdopodobieństwa Drobiazgi
Najogólniej mówiąc, kombinatoryka ekstremalna zajmuje się pytaniami o to, jaki jest rozmiar największego (lub najmniejszego) możliwego zbioru obiektów danego typu, spełniającego pewien zadany warunek i jak takie ekstremalne przypadki wyglądają.
Pozwolę sobie podtrzymać Czytelnika w napięciu i tytułowe pytanie tymczasem zostawię bez odpowiedzi. Zacznę za to od refleksji, czym jest płaskość.
Większość osób świadomych powiązań między światem matematyki a rzeczywistością zgodzi się, że na każdym kroku spotykamy się z rachunkiem prawdopodobieństwa. Oprócz niektórym dobrze znanych zagadnień związanych z grami losowymi pewne prawidłowości probabilistyczne możemy spotkać również w bardziej niespodziewanych miejscach.
Rozważmy następujący problem: gromadzimy powierzchnie wszystkich krajów wyrażone w kilometrach kwadratowych i patrzymy tylko na pierwsze cyfry znaczące tych wartości. Otrzymamy listę liczb z zakresu od 1 do 9 włącznie; pytanie brzmi, jakie są częstości ich występowania w tym zbiorze?
Zastosowania matematyki Epidemie
Prawie co roku w sezonie grypowym w mediach pojawia się temat szczepień. Omawiane są różne aspekty, podawane argumenty za i przeciw szczepieniom, często obserwujemy więcej emocji niż racjonalizmu. Epidemie, a w szczególności pandemie, stanowią przedmiot badań od wielu lat ze względu na swój znaczący wpływ na rozwój populacji ludzkiej. Zarówno w starożytności, jak i w średniowieczu, a także już w czasach współczesnych różnego typu choroby, takie jak dżuma, tyfus, cholera, grypa, dziesiątkowały mieszkańców naszego globu.
Grupa warkoczy była rozważana po raz pierwszy przez Adolfa Hurwitza w roku 1885, jednak nie pod tą nazwą; w grupie rozważanej przez Hurwitza trudno było dopatrzyć się warkoczy. Nazwę wprowadził Emil Artin w roku 1925, bo w jego interpretacji elementy grupy kojarzą się z warkoczami. Przypomnę, jak się je zaplata...
Oznaczmy przez 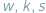 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 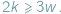 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 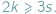 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: 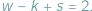
Rachunek prawdopodobieństwa Drobiazgi
W teorii prawdopodobieństwa mówimy o modelu klasycznym, gdy zbiór wszystkich zdarzeń elementarnych 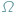 jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...
jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...
Dotarliśmy do ostatniej części cyklu, w którym prezentujemy wybrane przykłady zaskakujących relacji pomiędzy różnymi, pozornie bardzo odległymi, obszarami matematyki. Nie wypada jednak zakończyć bez poświęcenia należytej uwagi dziedzinie teorii liczb. Jak bowiem matematyka nazywana jest często królową nauk, tak o teorii liczb mówi się często jako o królowej matematyki. A królowa ma, oczywiście, wielu służących.
Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.
Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: 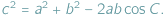 Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt
Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 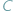 jest prosty, czyli
jest prosty, czyli