Delta mi!

Rozmaite zagadnienia można wygodnie i ładnie ilustrować geometrycznie. Jeśli wyniki doświadczenia losowego dają się zinterpretować jako punkty pewnego obszaru i każdy wynik jest jednakowo prawdopodobny, to prawdopodobieństwo określonego zdarzenia można wyznaczyć jako stosunek miary (pola, objętości etc.) odpowiadającej mu części obszaru do miary całości.

Równania algebraiczne, czyli takie, które można zapisać, przyrównując wielomian do zera, intrygowały ludzi od bardzo dawna. Rozwiązywaniem równań zajmowano się już w czasach starożytnych. W szkole uczą nas, jak rozwiązywać równania liniowe i kwadratowe, to jest takie, w których występuje funkcja liniowa (wielomian stopnia pierwszego) albo funkcja kwadratowa (wielomian stopnia drugiego). Matematycy włoscy podali w XVI wieku wzory na pierwiastki równań stopnia trzeciego i czwartego. A co z równaniami wyższych stopni?

Wbrew pozorom tytuł niniejszego tekstu nie jest efektem zestawienia dwóch przypadkowych słów; nawet zupełnie przypadkowe przypadki mogą zdradzać pewne regularności i fakt ten wcale ich przypadkowości nie przeczy. Przypadkiem ich praktycznego zastosowania są średniowieczne tablice do gry w kości; opisane w nich zasady faworyzują jedną ze stron w sposób na tyle delikatny, że oszukiwana strona wcale się taką nie czuje...

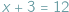Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 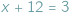wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 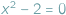nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 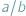zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną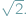

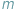Wielościan wypukły, którego ściany są jednakowymi wielokątami foremnymi, może mieć ściany trójkątne, czworokątne lub pięciokątne. Ostatnie dwa przypadki realizują się tylko w postaci sześcianu i dwunastościanu...

Ten artykuł będzie poświęcony zliczaniu różnych kolorowań obiektów, które podlegają symetrii. Wyobraźmy sobie, że Kalina chciałaby pokolorować rogi kwadratu za pomocą kolorów. Ile różnych figur może w ten sposób otrzymać?

Dwie nierównoległe płaszczyzny przecinają się wzdłuż prostej. Ta niepozorna obserwacja bywa bardzo przydatna.

Problem, który opiszę, został zaproponowany przez Amerykanów na LV Międzynarodową Olimpiadę Matematyczną, a jego treść brzmi następująco...

Gwiazdka foremna to łamana zamknięta, wpisana w okrąg i złożona z jednakowej długości cięciw, ale niebędąca wielokątem foremnym. Nie trzeba długo się zastanawiać, by stwierdzić, że odcinki takich łamanych muszą się przecinać.

Na pierwszym etapie XI Olimpiady Matematycznej Gimnazjalistów pojawiło się pytanie, na które tylko 24% uczestników odpowiedziało poprawnie...

Wiele przedmiotów zawdzięcza swe istnienie kompozycji dwóch pozornie niewspółistniejących ze sobą idei. Louis Braille połączył koncepcję zapisu graficznego, czyli odczytywanego za pomocą wzroku, ze sposobem zapisywania wiadomości zaprojektowanym dla ludzi niewidomych, którzy korzystają ze zmysłu dotyku. W rezultacie powstał alfabet dla niewidomych, który można odczytać także za pomocą wzroku. Podobnie narodził się pomysł na zbadanie obrazów inwersyjnych w różnych metrykach...

Zamiast analizować, czy gra jest sprawiedliwa, czy nie, zamiast szukać najlepszych strategii graczy, można stworzyć pewną maszynę, która część tej pracy wykona za nas. Trzeba jej objaśnić zasady, a potem z nią grać, niekoniecznie najlepiej - w końcu jeszcze nie przeanalizowaliśmy gry. Maszyna, grając, zapamiętując i wyciągając wnioski z przegranych oraz wygranych (co śmiało można zakwalifikować jako uczenie się), prędzej czy później zorientuje się, jak grać możliwie najlepiej, a więc ogrywać nas, o ile to tylko możliwe.

"Matematyka wedyjska" to umowna nazwa zbioru algorytmów, które można zastosować, aby rozwiązać pewne rachunkowe problemy. Reguły te zostały sformułowane w XX wieku przez hinduskiego duchownego Bharatiego Kriszna Tirtha, który twierdził, że są one zapisane w hinduskich świętych księgach, Wedach.

W tym krótkim artykule autorzy chcą zaprezentować zwięzły i piękny w swej prostocie dowód rozbieżności szeregu odwrotności liczb pierwszych. Fakt ten można udowadniać, razem z innymi fundamentalnymi i bardziej wyrafinowanymi twierdzeniami teorii liczb przez cały semestr przedmiotu Teoria Liczb, na Wydziale MIM UW, ale można go również wytłumaczyć w sposób elementarny.

Mówi się, że origami powstało dwa tysiące lat temu wraz z wynalezieniem papieru. W tym kontekście wydaje się zaskakujące, że początek odkrywania matematyki stojącej za składaniem papieru przypada dopiero na lata osiemdziesiąte zeszłego stulecia. Dziś gałąź nauki zwana origami obliczeniowe (ang. computational origami) rozwija się bardzo prężnie.

Czysty zeszyt, cyrkiel, linijka, kątomierz, liniuszek - standardowy szkolny ekwipunek lekcji geometrii. Ale istnieją również inne geometrie, w których do konstrukcji figur nie jest potrzebne żadne oprzyrządowanie. Jedną z nich jest geometria dziewięciu punktów, gdzie bez linijki czy cyrkla można "konstruować" całkiem dokładnie koła, trójkąty i inne figury.

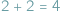Słyszy się często: "to pewne, jak ". Zdania matematyczne bywają podawane za wzór niewzruszonej i absolutnej prawdy. Pytanie, jakie zdania? Niewątpliwie pewniki, czyli aksjomaty ("przez dwa punkty przechodzi dokładnie jedna prosta") oraz twierdzenia, choćby tak łatwe, jak to zacytowane na początku.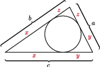

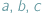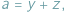
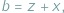
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków pewnego trójkąta, często przydaje się podstawienie Raviego: 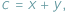gdzie 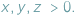Takie liczby 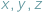zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.