
Niby nic
W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.

W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.
Sztuczna inteligencja Migawki informatyczne
Drogi Czytelniku Majsterkowiczu! W tym odcinku Migawki wreszcie będzie ciekawie. Opiszemy, jak samodzielnie skonstruować prawdziwy zegarek mechaniczny!
Chciałbym opowiedzieć o najtrudniejszym pojęciu matematyki. Najtrudniejszym, choć intuicyjnie prostym i używanym powszechnie również przez niematematyków. Chodzi o orientację...
Jedna z rzeczy, które trudno wytłumaczyć niematematykom, to dowody niekonstruktywne. W takim dowodzie autorzy dochodzą do wniosku, iż pewien obiekt matematyczny istnieje, często wiedząc o nim bardzo mało. Dzieje się tak dlatego, że stwierdzamy istnienie takiego obiektu, nie próbując go skonstruować, tylko powołując się na inne fakty. Jednym z najprostszych przykładów jest dowód przez "kradzież strategii", który pokażę na przykładzie prostej gry.
Tym razem będziemy wycinać...
W tym artykule chcemy zaprezentować pewną technikę dowodową zwaną interpretacją kombinatoryczną. Metoda ta pokazana będzie w działaniu: podajemy dwa zadania wraz z rozwiązaniami, które są ilustracją tematu.
Małe Twierdzenie Fermata ma również taki dowód...
Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.
Twierdzenie Talesa dowieść można bez trudu...
Udowodnijmy lub obalmy twierdzenie: istnieją takie liczby niewymierne 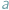 i
i 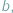 że
że 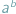 jest liczbą wymierną.
jest liczbą wymierną.
Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.
Zbiór wszystkich liczb rzeczywistych 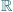 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 

Paradoks Banacha-Tarskiego (1924 r.). Kulę można rozłożyć na skończenie wiele części, z których da się zbudować dwie takie same kule.
Podwojenie sześcianu to zadanie: skonstruuj odcinek 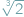 razy dłuższy od danego...
razy dłuższy od danego...
Grając w większość gier karcianych, musimy przetasować talię w taki sposób, aby ich kolejność była "jak najbardziej" losowa. Pierwszym pytaniem, na które odpowiemy sobie w tym artykule, jest pytanie o probabilistyczny sposób wyrażenia tej własności.
Tradycyjnie fraktale kojarzą nam się (często) z ładnymi rysunkami figur, które wykazują pewien zestaw cech odróżniających je od zwykłych obiektów. Nie precyzujemy tutaj uniwersalnego zestawu, gdyż sama definicja fraktala nie jest uniwersalna. W większości sytuacji chcemy, aby fraktal miał złożoną strukturę, spełniał pewne cechy samopodobieństwa oraz by nie dało się go zbyt prosto opisać geometrycznie. Mimo to często można go opisać względnie prosto pewnymi regułami rekurencyjnymi wykonywanymi na obiekcie startowym (lub zestawie takich obiektów).
Pętle na rysunku 1 przedstawiają ten sam sznurek...
Cytat z General Relativity Johna Archibalda Wheelera, który został umieszczony u góry marginesu artykułu Michała Bejgera, można przejrzyście zilustrować geometrycznie, gdy zajmiemy się przestrzenią dwuwymiarową.

Dlaczego w szkole tak dużo uczymy się o wielomianach? Są dwa podstawowe powody. Pierwszy z nich - całkiem zrozumiały - po prostu jest to niemal największa klasa funkcji, których wartości umiemy obliczać. Potrafimy jeszcze dzielić wartości wielomianów, ale z pozostałymi funkcjami, które występują w programie szkolnym, a później na studiach, w zasadzie mielibyśmy sporo problemów.
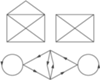
Rys. 1 (a), (b), (c). Linie oznaczone strzałkami można rysować tylko zgodnie z ich kierunkiem
Które z rysunków 1 (a), (b), (c) da się narysować bez odrywania ołówka od kartki i bez rysowania ponownie wzdłuż narysowanej już linii?