Twierdzenie o czterech kolorach

Jest w matematyce wiele twierdzeń, których znaczenie jest o wiele większe, aniżeli tylko wynik w nich zawarty. Są one swoistymi legendami i najwyrazistszymi przedstawicielami różnych dziedzin matematyki. Aby jednak twierdzenie (czy też hipoteza) miały szanse stać się taką legendą i na trwałe zapisać się w historii matematyki, muszą być spełnione dwa podstawowe warunki. Po pierwsze, teza takiego twierdzenia powinna dać się sformułować w prostym, czasem wręcz potocznym języku zrozumiałym nie tylko dla specjalistów, ale także dla przeciętnego odbiorcy zainteresowanego matematyką. Po drugie, chyba ważniejsze, dowód takiego prosto sformułowanego twierdzenia nie powinien być łatwo i szybko znaleziony. Im dłużej twierdzenie pozostaje hipotezą, im więcej słynnych matematyków bezskutecznie poszukuje dowodu, tym większa szansa, że przejdzie ono do historii jako twierdzenie–legenda.

Można by zaryzykować stwierdzenie, że każda dziedzina matematyki ma w swoim dorobku co najmniej jedno takie twierdzenie. W teorii grafów jest nim twierdzenie o czterech barwach, którego historia sięga roku 1852, kiedy to student Francis Guthrie, wiedziony czysto praktycznymi pobudkami, postawił swemu wykładowcy, Augustowi De Morganowi, następujące pytanie: jaka jest najmniejsza liczba kolorów, która wystarcza do pokolorowania dowolnej płaskiej mapy w taki sposób, aby każde dwa państwa, które graniczą ze sobą, otrzymały różne kolory?

Korzystając z twierdzenia Eulera o wielościanach, nietrudno stwierdzić, że 6 kolorów wystarcza. Nieco bardziej zaawansowaną techniką można zmniejszyć tę liczbę do 5. Z drugiej strony istnieją mapy, dla których 3 kolory to za mało. I tak sformułowano hipotezę, którą zdała się potwierdzać praktyka. Każdą mapę na płaszczyźnie można poprawnie pokolorować przy użyciu czterech kolorów. Hipoteza szybko stała się sławna, gdyż mimo prostego sformułowania nijak nie dawała się prosto udowodnić ani też obalić.

Pierwszy „dowód” podał w 1879 roku Alfred Bray Kempe i od tej chwili świat nauki uznał problem za rozwiązany, a autora dowodu uhonorowano nawet wieloma zaszczytami. Jednak w 1890 roku Percy John Heawood znalazł w dowodzie Kempego błąd na tyle poważny, że nie dało się go usunąć i tak twierdzenie o czterech barwach z powrotem stało się hipotezą. Po tym wydarzeniu zainteresowanie problemem wzrosło wielokrotnie, przez kolejne dziesiątki lat wielu matematyków zmagało się z nim bezskutecznie. Osiągano pewne częściowe wyniki (na przykład podnoszono sukcesywnie liczbę państw na mapie, które na pewno dadzą się pokolorować 4 barwami), analizowano coraz większą liczbę nowych przypadków, jednak formalny ścisły dowód nadal pozostawał poza zasięgiem ludzkich umysłów. Dopiero po upływie 124 lat, w 1976 roku Kenneth Appel i Wolfgang Haken przedstawili wielostronicowy dowód polegający na redukcji problemu do wielogodzinnej komputerowej analizy około dwóch tysięcy pojedynczych przypadków.

Zamiast spodziewanego uczucia ulgi i radości, że ponad stuletni problem został w końcu rozwiązany, rozpętała się prawdziwa burza na pograniczu matematyki i filozofii. Zaczęto stawiać fundamentalne pytania, co właściwie może być uznane za dowód twierdzenia, czy dowód niemożliwy do weryfikacji przez człowieka może być uznany za wiarygodny i dla kogo właściwie dowodzimy twierdzenia: dla ludzi czy dla komputerów. Na domiar złego okazało się, że dowód ów zawiera kilka istotnych luk. Jednak po kolejnych poprawkach i redukcji liczby przypadków do zaledwie kilkuset oraz kolejnej publikacji matematycy uznali twierdzenie o czterech kolorach za udowodnione, choć pewien niedosyt pozostał i jeszcze z pewnością wielu matematyków nie spocznie w wysiłkach w poszukiwaniu „dowodu z Księgi” lub choćby takiego, którego weryfikacja nie będzie wymagać użycia komputera.

Kolorowanie map jako gra

W przeszłości często zdarzało się tak, że skomplikowanie prostego problemu lub sformułowanie go w ogólniejszej postaci prowadziło do jego rozwiązania (było tak np. z Wielkim Twierdzeniem Fermata). W roku 1981 profesor nauk politycznych z Uniwersytetu Nowojorskiego, Steven Brams, wiedziony nadzieją, że da się w ten sposób znaleźć inny, łatwiejszy dowód twierdzenia o czterech kolorach, postanowił problem kolorowania map nieco skomplikować. Wpadł on na pomysł, żeby kolorowanie danej mapy odbywało się jako dwuosobowa gra o bardzo prostych regułach.

Niech dwaj gracze, Jacek i Placek (oryginalnie Minimizer i Maximizer), na przemian kolorują regiony (państwa) zadanej mapy, mając do dyspozycji ustalony (ten sam dla obu) zbiór kolorów. Grę rozpoczyna Jacek i jego celem jest takie wybieranie regionów i kolorów, aby cała mapa została w końcu poprawnie pokolorowana. Natomiast jego przeciwnik, Placek, chce za wszelką cenę temu zapobiec. Jednak obu graczy obowiązuje ta sama reguła, że w każdym momencie gry regiony, które graniczą ze sobą, muszą mieć nadane różne kolory. Jacek zwycięża, gdy cała mapa została poprawnie pokolorowana, Placek zaś w przeciwnym przypadku.

Idee Bramsa opublikował w 1981 roku Martin Gardner w swojej rubryce w „Scientific American”, stawiając jednocześnie pytanie, jaka jest najmniejsza liczba kolorów, która zapewni Jackowi zwycięstwo na dowolnej mapie. Pokazanie, że 4 kolory mu nie wystarczą, jest proste. Wystarczy jako mapę wziąć model sześcianu, strategia Placka zaś polegać będzie na tym, że w swoim ruchu koloruje on zawsze ścianę przeciwległą do tej, którą uprzednio pokolorował Jacek, używając do tego celu nieużytego wcześniej koloru.

W jednym z kolejnych numerów Lloyd Shapley pokazał, że również 5 kolorów nie zagwarantuje Jackowi zwycięstwa. Tym razem gra toczy się na modelu dwunastościanu foremnego. Strategia Placka ponownie polega na tym, aby kolorować przeciwległą ścianę, lecz tym razem robi on to zawsze tym samym kolorem, którego użył Jacek w poprzednim ruchu. Patrząc na dwunastościan foremny, łatwo zauważyć, że Jacek jest zmuszony w kolejnych swoich ruchach używać nowego koloru, a co za tym idzie – nie jest w stanie wygrać gry na 5 kolorach.

W następnym numerze Robert High podał przykład 20-ściennej mapy (ponownie był to model bryły), dla której nawet 6 kolorów nie zagwarantuje Jackowi zwycięstwa. Jednocześnie postawił hipotezę, że 7 kolorów wystarczy Jackowi do zwycięstwa na każdej mapie, choć z drugiej strony nie było nawet wiadomo, czy jakakolwiek skończona liczba kolorów może mu to zagwarantować. Więcej publikacji na ten temat nie było, więc hipoteza Higha pozostała otwarta.

W 1991 roku Hans Bodlaender opublikował pracę „O złożoności pewnych gier w kolorowanie”, w której opisał dwuosobową grę w kolorowanie wierzchołków dowolnego skończonego grafu. Gracze noszą tym razem imiona Alice i Bob, lecz reguły gry są grafowym odpowiednikiem reguł Bramsa. Autor wprowadził ponadto parametr 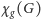zwany rozgrywaną liczbą chromatyczną (ang. game chromatic number), a zdefiniowany jako najmniejsza liczba kolorów, dla której Alice (Jacek) ma zwycięską strategię na grafie 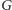 . Postawił też hipotezę, że 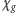jest skończona na klasie wszystkich grafów planarnych, które są odpowiednikiem map na płaszczyźnie. Nie pokusił się jednak o podanie żadnej stałej, która miałaby być ograniczeniem, mimo że High próbował ją podać już 10 lat wcześniej.

Po tej publikacji specjaliści z teorii grafów żywo zainteresowali się problemem gry w kolorowanie. W 1994 roku Hal Kierstead i William Trotter pozytywnie zweryfikowali hipotezę Bodlaendera, podając pierwsze górne oszacowanie: 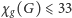dla każdego grafu planarnego 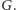Obalili przy okazji hipotezę Higha, znajdując graf planarny, dla którego 7 kolorów nie gwarantuje Alice zwycięstwa.

W 5 lat później ukazuje się praca Thomasa Dinsky’ego i Xudinga Zhu, w której podają oni zaskakująco prosty i elegancki dowód nieco lepszego oszacowania 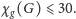Wkrótce Zhu obniża to oszacowanie do 19, używając skomplikowanej metody aktywacji. Następnie Kierstead poprawia ten wynik o 1. Aktualny rekord wynosi 17 kolorów i należy ponownie do Zhu. Biorąc pod uwagę dystans pomiędzy 8 a 17, oraz rosnącą komplikację stosowanych technik dowodowych, należy sądzić, że wyścig ten nieprędko się skończy i pewnie jeszcze długo przyjdzie nam czekać na ostateczne rozwiązanie tego intrygującego problemu.

Wątek sensacyjny

Przy tej okazji warto wspomnieć o pewnym niecodziennym fakcie. Otóż we wszystkich publikacjach traktujących o grze w kolorowanie grafów jako twórca gry podawany jest Bodlaender, mimo że 10 lat wcześniej, grę tę wymyślił Brams. Rzecz jasna, matematycy zawsze oddają należną cześć twórcom oryginalnych problemów, a że tym razem tak się nie stało, wynika po prostu z faktu, iż żaden z autorów publikacji nie miał pojęcia o Stevenie Bramsie i jego pomysłach opublikowanych w czasopiśmie popularnonaukowym.

Niedopatrzenie to zostanie już wkrótce naprawione. Pierwszym krokiem w tym kierunku jest niniejszy artykuł, „Delta” zaś jest prawdopodobnie pierwszym czasopismem na świecie, w którym cała historia związana z grą w kolorowanie zostaje przedstawiona. Autorom udało się także nawiązać bezpośredni kontakt zarówno z Bramsem, jak i Kiersteadem oraz Zhu, którzy zapowiedzieli, że już w kolejnych swoich publikacjach wspomną o pierwszym autorze pomysłu na grę w kolorowanie.

Najzabawniejszy w całej sprawie wydaje się jednak fakt, że, jak nam doniósł z niekłamanym żalem S. Brams, przez wiele lat usiłował on zainteresować wielu matematyków tym problemem, jednak bez rezultatu. Nasuwa się więc refleksja, że być może warto częściej sięgać po czasopisma popularne typu „Delta” czy „Świat Nauki”, gdyż mogą się one okazać prawdziwą skarbnicą pomysłów i źródłem inspiracji do poważnych rozpraw naukowych.