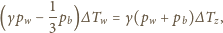Klub 44F - zadania XII 2015»Zadanie 608
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania XII 2015
- Publikacja w Delcie: grudzień 2015
- Publikacja elektroniczna: 30 listopada 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (98 KB)

Taśma transportera o długości 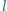 porusza się z prędkością
porusza się z prędkością 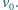 Z jaką prędkością
Z jaką prędkością  względem Ziemi należy popchnąć mały klocek z końca transportera przeciwnie do ruchu taśmy, aby ilość ciepła wydzielona w wyniku tarcia klocka o taśmę była największa? Jaka jest wartość tego ciepła, jeżeli współczynnik tarcia wynosi
względem Ziemi należy popchnąć mały klocek z końca transportera przeciwnie do ruchu taśmy, aby ilość ciepła wydzielona w wyniku tarcia klocka o taśmę była największa? Jaka jest wartość tego ciepła, jeżeli współczynnik tarcia wynosi 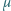 i spełniony jest warunek
i spełniony jest warunek 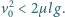
 otrzymujemy z zależności
otrzymujemy z zależności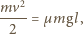
 jest masą klocka. Stąd
jest masą klocka. Stąd 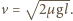 Po zatrzymaniu klocek zaczyna poruszać się z przyspieszeniem
Po zatrzymaniu klocek zaczyna poruszać się z przyspieszeniem 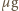 w kierunku ruchu taśmy. Prędkość taśmy osiągnie po czasie
w kierunku ruchu taśmy. Prędkość taśmy osiągnie po czasie 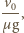 gdy przebędzie względem Ziemi drogę
gdy przebędzie względem Ziemi drogę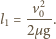
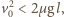 klocek osiągnie prędkość
klocek osiągnie prędkość 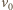 względem Ziemi, czyli zatrzyma się względem taśmy, zanim spadnie z transportera. Energia kinetyczna klocka w układzie związanym z taśmą transportera od chwili startu do chwili zatrzymania maleje o wielkość
względem Ziemi, czyli zatrzyma się względem taśmy, zanim spadnie z transportera. Energia kinetyczna klocka w układzie związanym z taśmą transportera od chwili startu do chwili zatrzymania maleje o wielkość 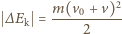 i tyle wynosi maksymalne ciepło wydzielone w układzie:
i tyle wynosi maksymalne ciepło wydzielone w układzie: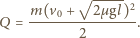
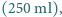 która na początku ma
która na początku ma 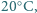 przy użyciu energii z baterii w rozmiarze AA. Dobrej jakości bateria, kosztująca około 2 zł, podając prąd
przy użyciu energii z baterii w rozmiarze AA. Dobrej jakości bateria, kosztująca około 2 zł, podając prąd 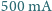 przy napięciu
przy napięciu 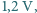 wyczerpuje się po około godzinie. Ile razy taniej jest użyć do tego celu energii z sieci (cena
wyczerpuje się po około godzinie. Ile razy taniej jest użyć do tego celu energii z sieci (cena 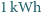 to około
to około 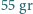 )?
)?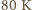 to:
to: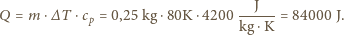
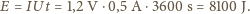
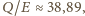 czyli potrzebujemy 39 baterii, których koszt to około
czyli potrzebujemy 39 baterii, których koszt to około 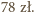 Koszt podgrzania energią z sieci:
Koszt podgrzania energią z sieci: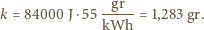
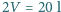 rozdzielone jest na dwie równe części nieruchomą przegrodą. Do jednej części naczynia wprowadzono argon o masie
rozdzielone jest na dwie równe części nieruchomą przegrodą. Do jednej części naczynia wprowadzono argon o masie 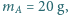 do drugiej wodór o masie
do drugiej wodór o masie 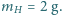 Przez przegrodę może przenikać tylko wodór. Jakie ciśnienia ustalą się w obu częściach naczynia po ustaleniu się stanu równowagi? Temperatura w części naczynia zawierającej argon wynosi
Przez przegrodę może przenikać tylko wodór. Jakie ciśnienia ustalą się w obu częściach naczynia po ustaleniu się stanu równowagi? Temperatura w części naczynia zawierającej argon wynosi 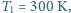 w drugiej części
w drugiej części 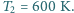 Masy molowe argonu i wodoru są odpowiednio równe
Masy molowe argonu i wodoru są odpowiednio równe 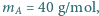
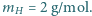
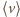 ruchu cieplnego cząsteczek. W danej temperaturze zachodzi związek
ruchu cieplnego cząsteczek. W danej temperaturze zachodzi związek 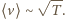 Oznaczmy przez
Oznaczmy przez 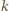 liczbę moli wodoru, które przeniknęły przez przegrodę. Warunek równowagi ma postać:
liczbę moli wodoru, które przeniknęły przez przegrodę. Warunek równowagi ma postać: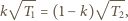
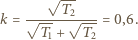
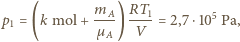
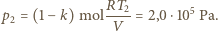
 moli jednoatomowego gazu doskonałego o temperaturze
moli jednoatomowego gazu doskonałego o temperaturze 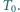 Układ jest izolowany cieplnie od otoczenia. Gaz ściśnięto za pomocą tłoka, wykonując nad gazem pracę
Układ jest izolowany cieplnie od otoczenia. Gaz ściśnięto za pomocą tłoka, wykonując nad gazem pracę 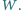 Następnie tłok puszczono i zatrzymał się on w nowym położeniu równowagi. Jaka jest temperatura końcowa gazu? Ciśnienie zewnętrzne jest stałe.
Następnie tłok puszczono i zatrzymał się on w nowym położeniu równowagi. Jaka jest temperatura końcowa gazu? Ciśnienie zewnętrzne jest stałe.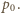 Oznaczmy objętości i temperatury gazu w kolejnych stanach równowagi przez
Oznaczmy objętości i temperatury gazu w kolejnych stanach równowagi przez 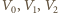 oraz
oraz 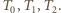 Zmiana energii wewnętrznej podczas ściskania gazu wynosi
Zmiana energii wewnętrznej podczas ściskania gazu wynosi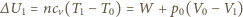
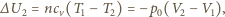
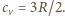 Całkowita zmiana energii wewnętrznej
Całkowita zmiana energii wewnętrznej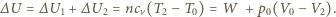
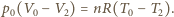
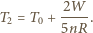
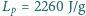 i napięcia powierzchniowego woda-powietrze (energia jednostki powierzchni swobodnej wody)
i napięcia powierzchniowego woda-powietrze (energia jednostki powierzchni swobodnej wody) 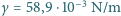 (w
(w 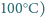 oszacuj liczbę cząsteczek wody w
oszacuj liczbę cząsteczek wody w 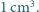 Gęstość wody
Gęstość wody 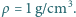
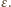
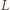 zawierającym
zawierającym 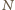 cząsteczek wynosi
cząsteczek wynosi 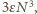 bo każda cząsteczka ma 6 najbliższych sąsiadów i z każdym dzieli jedno wiązanie. Do oddzielenia dwóch sąsiednich warstw cząsteczek potrzebna jest energia
bo każda cząsteczka ma 6 najbliższych sąsiadów i z każdym dzieli jedno wiązanie. Do oddzielenia dwóch sąsiednich warstw cząsteczek potrzebna jest energia 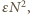 ale po rozdzieleniu powstają dwie kwadratowe powierzchnie swobodne cieczy o boku o długości
ale po rozdzieleniu powstają dwie kwadratowe powierzchnie swobodne cieczy o boku o długości 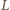 każda. Mamy więc
każda. Mamy więc 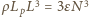 oraz
oraz 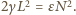 Stąd już łatwo wyznaczamy:
Stąd już łatwo wyznaczamy: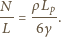
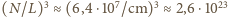 cząsteczek w
cząsteczek w 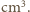 Dokładna wartość to 1/18 liczby Avogadro, czyli
Dokładna wartość to 1/18 liczby Avogadro, czyli 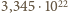 cząsteczek w
cząsteczek w 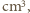 a więc otrzymaliśmy niezły wynik.
a więc otrzymaliśmy niezły wynik.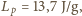
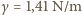 - dla powierzchni (w
- dla powierzchni (w 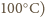 - oraz
- oraz 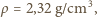 dla którego otrzymujemy wartość
dla którego otrzymujemy wartość 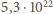 atomów w
atomów w 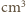 wobec dokładnej wartości
wobec dokładnej wartości 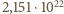 - tu rozbieżność wynika z nieco bardziej skomplikowanej postaci sieci krystalicznej niż przyjęta w naszych obliczeniach.
- tu rozbieżność wynika z nieco bardziej skomplikowanej postaci sieci krystalicznej niż przyjęta w naszych obliczeniach.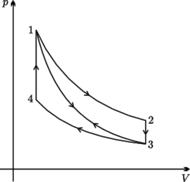
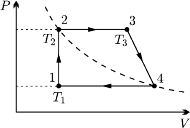
 są przemianami izotermicznymi. Proces 1-3 jest przemianą adiabatyczną. Procesy 2-3 oraz 4-1 to izochory. Sprawność cyklu 1-2-3-1 wynosi
są przemianami izotermicznymi. Proces 1-3 jest przemianą adiabatyczną. Procesy 2-3 oraz 4-1 to izochory. Sprawność cyklu 1-2-3-1 wynosi 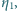 sprawność cyklu 1-3-4-1 wynosi
sprawność cyklu 1-3-4-1 wynosi 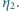 Oblicz sprawność cyklu 1-2-3-4-1.
Oblicz sprawność cyklu 1-2-3-4-1.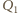 ciepło pobrane na izotermie 1-2, a przez
ciepło pobrane na izotermie 1-2, a przez 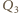 wartość bezwzględną ciepła oddanego na izotermie 3-4. Na wykresie
wartość bezwzględną ciepła oddanego na izotermie 3-4. Na wykresie 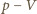 są one równe polu pod odpowiednią izotermą, bo w przemianie izotermicznej energia wewnętrzna nie zmienia się. Zatem praca uzyskana w cyklu 1-2-3-4-1 wynosi
są one równe polu pod odpowiednią izotermą, bo w przemianie izotermicznej energia wewnętrzna nie zmienia się. Zatem praca uzyskana w cyklu 1-2-3-4-1 wynosi 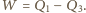 Sprawność tego cyklu
Sprawność tego cyklu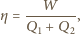
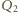 jest ciepłem pobranym na izochorze 4-1. Jest ono równe wartości bezwzględnej ciepła oddanego na izochorze 2-3, bo obie izochory łączą na wykresie
jest ciepłem pobranym na izochorze 4-1. Jest ono równe wartości bezwzględnej ciepła oddanego na izochorze 2-3, bo obie izochory łączą na wykresie  punkty o tych samych temperaturach. Sprawność cyklu 1-2-3-1 dana jest wzorem
punkty o tych samych temperaturach. Sprawność cyklu 1-2-3-1 dana jest wzorem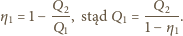
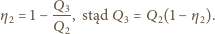
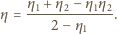
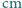 wypełniono całkowicie wodą i umieszczono w pokoju, w którym nie ma prądów powietrza. Przez dwie doby poziom wody w akwarium obniżył się o 1 centymetr. Przyjmując, że temperatura i wilgotność powietrza w pokoju są stałe, a proces parowania jest na tyle powolny, że temperatura wody nie ulega zmianie, znaleźć czas, po którym woda całkowicie wyparuje z akwarium.
wypełniono całkowicie wodą i umieszczono w pokoju, w którym nie ma prądów powietrza. Przez dwie doby poziom wody w akwarium obniżył się o 1 centymetr. Przyjmując, że temperatura i wilgotność powietrza w pokoju są stałe, a proces parowania jest na tyle powolny, że temperatura wody nie ulega zmianie, znaleźć czas, po którym woda całkowicie wyparuje z akwarium.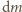 parująca w bardzo krótkim czasie
parująca w bardzo krótkim czasie 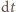 jest proporcjonalna do pola powierzchni wody
jest proporcjonalna do pola powierzchni wody 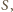 czyli
czyli 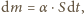 gdzie
gdzie 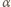 jest współczynnikiem proporcjonalności. Zmiana poziomu wody w akwarium
jest współczynnikiem proporcjonalności. Zmiana poziomu wody w akwarium 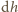 wiąże się ze zmianą jej masy zależnością
wiąże się ze zmianą jej masy zależnością 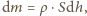 gdzie
gdzie 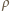 - gęstość wody. Stąd
- gęstość wody. Stąd 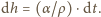 Tak więc w stałych warunkach parowania zmiana poziomu wody jest proporcjonalna do czasu. Jeżeli więc przez dwie doby poziom wody obniżył się o 1 centymetr, to cała woda, przy głębokości akwarium równej 15
Tak więc w stałych warunkach parowania zmiana poziomu wody jest proporcjonalna do czasu. Jeżeli więc przez dwie doby poziom wody obniżył się o 1 centymetr, to cała woda, przy głębokości akwarium równej 15 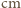 , wyparuje po 30 dobach.
, wyparuje po 30 dobach.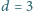 mm. Jakie powinno być ciśnienie zawartego w niej gazu, żeby jej
zapłon (zaświecenie) następował po przyłożeniu napięcia 100 V. Energia
jonizacji neonu wynosi
mm. Jakie powinno być ciśnienie zawartego w niej gazu, żeby jej
zapłon (zaświecenie) następował po przyłożeniu napięcia 100 V. Energia
jonizacji neonu wynosi
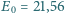 eV. Przyjmij, że temperatura gazu
w lampie wynosi
eV. Przyjmij, że temperatura gazu
w lampie wynosi
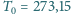 K. W warunkach normalnych droga
swobodna elektronu w neonie wynosi
K. W warunkach normalnych droga
swobodna elektronu w neonie wynosi
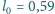
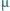 m.
m.
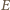 :
:
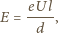
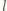 oznacza drogę swobodną elektronu (patrz zadanie 855),
oznacza drogę swobodną elektronu (patrz zadanie 855),
 ładunek elektronu, a
ładunek elektronu, a
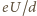 jest równe natężeniu pola
elektrycznego pomiędzy elektrodami. Oznacza to, że droga swobodna elektronu
powinna wynosić:
jest równe natężeniu pola
elektrycznego pomiędzy elektrodami. Oznacza to, że droga swobodna elektronu
powinna wynosić:
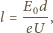
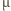 m. Droga swobodna jest odwrotnie proporcjonalna
do ciśnienia gazu, a więc w neonówce powinno panować ciśnienie
m. Droga swobodna jest odwrotnie proporcjonalna
do ciśnienia gazu, a więc w neonówce powinno panować ciśnienie
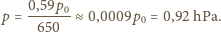
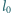 (tzw. średnią drogę swobodną)
przebywaną przez elektron pomiędzy dwoma zderzeniami z atomami
neonu znajdującego się w warunkach normalnych (tj. w temperaturze
(tzw. średnią drogę swobodną)
przebywaną przez elektron pomiędzy dwoma zderzeniami z atomami
neonu znajdującego się w warunkach normalnych (tj. w temperaturze
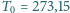 K i pod ciśnieniem
K i pod ciśnieniem
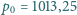 hPa). Promień
atomu neonu wynosi
hPa). Promień
atomu neonu wynosi
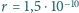 m.
m.
 od toru ruchu elektronu.
średnio nastąpi to, gdy w objętości
od toru ruchu elektronu.
średnio nastąpi to, gdy w objętości
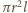 będzie znajdował się jeden
atom. Oznacza to warunek
będzie znajdował się jeden
atom. Oznacza to warunek
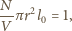
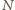 jest liczbą atomów, a
jest liczbą atomów, a
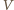 objętością naczynia. Dla gazu
w warunkach normalnych mamy
objętością naczynia. Dla gazu
w warunkach normalnych mamy
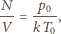
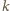 jest stałą Boltzmanna. Ostatecznie:
jest stałą Boltzmanna. Ostatecznie:
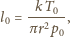
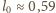
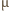 m.
m.
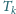 gazu
w szklance w chwili zgaśnięcia świeczki, jeśli na końcu doświadczenia,
w walcowej szklance o wysokości
gazu
w szklance w chwili zgaśnięcia świeczki, jeśli na końcu doświadczenia,
w walcowej szklance o wysokości
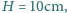 wysokość słupa wody
wynosiła
wysokość słupa wody
wynosiła
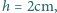 a temperatura w pomieszczeniu była równa
a temperatura w pomieszczeniu była równa
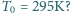 Głównym składnikiem współczesnych świec jest
mieszanina węglowodorów
Głównym składnikiem współczesnych świec jest
mieszanina węglowodorów
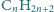 o
o
 w zakresie od 20 do
40.
w zakresie od 20 do
40.
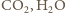 i CO. Z każdej cząsteczki tlenu powstają więc jedna lub
dwie cząsteczki produktów spalania, a więc w wyniku spalania tlenu
wzrasta liczba cząsteczek gazu. Dodatkowo wydzielone ciepło spalania
ogrzewa gaz. Oba zjawiska prowadzą do „ucieczki” części gazu spod
szklanki. Gdy świeczka zgaśnie, ilość gazu już się nie zmienia,
a jego stygnięcie (do temperatury otoczenia
i CO. Z każdej cząsteczki tlenu powstają więc jedna lub
dwie cząsteczki produktów spalania, a więc w wyniku spalania tlenu
wzrasta liczba cząsteczek gazu. Dodatkowo wydzielone ciepło spalania
ogrzewa gaz. Oba zjawiska prowadzą do „ucieczki” części gazu spod
szklanki. Gdy świeczka zgaśnie, ilość gazu już się nie zmienia,
a jego stygnięcie (do temperatury otoczenia
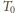 ) powoduje spadek
ciśnienia, co dalej prowadzi do zasysania wody z talerza. Ponieważ
wysokość słupa wody
) powoduje spadek
ciśnienia, co dalej prowadzi do zasysania wody z talerza. Ponieważ
wysokość słupa wody
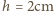 odpowiada różnicy ciśnień równej
jedynie około
odpowiada różnicy ciśnień równej
jedynie około
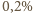 ciśnienia atmosferycznego, to z dobrym
przybliżeniem można przyjąć, że gaz w chwili zgaśnięcia świeczki i po
ostygnięciu do temperatury otoczenia znajdował się pod ciśnieniem
atmosferycznym. Masa gazu podczas stygnięcia nie zmienia się, a więc
stosunek temperatur równy jest stosunkowi objętości – dla szklanki
w kształcie walca równego stosunkowi wysokości części wypełnionych
gazem
ciśnienia atmosferycznego, to z dobrym
przybliżeniem można przyjąć, że gaz w chwili zgaśnięcia świeczki i po
ostygnięciu do temperatury otoczenia znajdował się pod ciśnieniem
atmosferycznym. Masa gazu podczas stygnięcia nie zmienia się, a więc
stosunek temperatur równy jest stosunkowi objętości – dla szklanki
w kształcie walca równego stosunkowi wysokości części wypełnionych
gazem
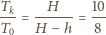
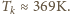
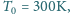 zaś
zaś
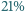 objętości pomieszczenia wypełniał tlen. Spalaniu węgla do
dwutlenku węgla towarzyszy wydzielenie ciepła
objętości pomieszczenia wypełniał tlen. Spalaniu węgla do
dwutlenku węgla towarzyszy wydzielenie ciepła
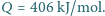 Jaka była
wysokość warstwy pyłu węglowego leżącego początkowo na podłodze, jeśli
pomieszczenie miało wysokość
Jaka była
wysokość warstwy pyłu węglowego leżącego początkowo na podłodze, jeśli
pomieszczenie miało wysokość
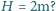 Można przyjąć, że
Można przyjąć, że
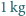 pyłu czystego węgla wypełnia objętość
pyłu czystego węgla wypełnia objętość
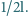
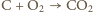 nie zmieni się liczba moli
gazu w pomieszczeniu, zostanie on jednak ogrzany do wysokiej temperatury. Dla
cząsteczek liniowych, takich jak
nie zmieni się liczba moli
gazu w pomieszczeniu, zostanie on jednak ogrzany do wysokiej temperatury. Dla
cząsteczek liniowych, takich jak
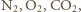 ciepło właściwe w stałej
objętości wynosi
ciepło właściwe w stałej
objętości wynosi
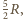 gdzie
gdzie
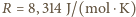 jest
stałą gazową. Energia wewnętrzna
jest
stałą gazową. Energia wewnętrzna
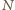 moli gazu jest zatem równa
moli gazu jest zatem równa
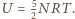 Bilans energii można zatem zapisać jako:
Bilans energii można zatem zapisać jako:

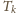 jest temperaturą końcową. Stąd
jest temperaturą końcową. Stąd
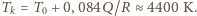 Zaniedbaliśmy tu fakt, że w wysokich
temperaturach poza stopniami swobody ruchu postępowego i rotacyjnego
cząsteczek gazu wzbudzane są także ich oscylacje, co prowadzi do zwiększenia
liczby stopni swobody: z 5 do 6 dla cząsteczek
Zaniedbaliśmy tu fakt, że w wysokich
temperaturach poza stopniami swobody ruchu postępowego i rotacyjnego
cząsteczek gazu wzbudzane są także ich oscylacje, co prowadzi do zwiększenia
liczby stopni swobody: z 5 do 6 dla cząsteczek
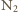 i z 5 do 9 dla
cząsteczek
i z 5 do 9 dla
cząsteczek
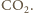 Uwzględnienie tego faktu w bilansie energii zmniejszy
oszacowanie
Uwzględnienie tego faktu w bilansie energii zmniejszy
oszacowanie
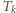 o około
o około
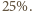 Wysokość warstwy pyłu to
(
Wysokość warstwy pyłu to
(
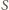 jest powierzchnią podłogi):
jest powierzchnią podłogi):
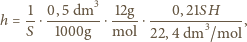
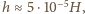 czyli około
czyli około
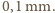
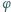 leży ołowiana blacha.
Współczynnik tarcia ołowiu o dach to
leży ołowiana blacha.
Współczynnik tarcia ołowiu o dach to
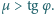 Współczynnik
rozszerzalności liniowej ołowiu wynosi
Współczynnik
rozszerzalności liniowej ołowiu wynosi
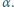 Zakładamy, że temperatura
w ciągu doby wzrasta od wartości
Zakładamy, że temperatura
w ciągu doby wzrasta od wartości
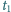 do
do
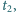 a potem ponownie
obniża się do
a potem ponownie
obniża się do
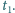 Długość blachy przy minimalnej temperaturze
Długość blachy przy minimalnej temperaturze
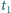 jest równa
jest równa
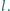 Na jaką odległość blacha spełznie z dachu
w ciągu doby?
Na jaką odległość blacha spełznie z dachu
w ciągu doby?
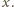 Siła tarcia działająca na
wydłużającą się blachę poniżej punktu nieruchomego działa w górę równi
i wynosi
Siła tarcia działająca na
wydłużającą się blachę poniżej punktu nieruchomego działa w górę równi
i wynosi
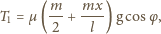
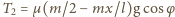 działa w dół
równi. Warunek równowagi statycznej dla punktu nieruchomego ma
postać:
działa w dół
równi. Warunek równowagi statycznej dla punktu nieruchomego ma
postać:
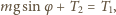
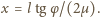 Wydłużenie blachy podczas ogrzewania wynosi
Wydłużenie blachy podczas ogrzewania wynosi
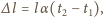 a jej środek przesuwa się w dół o
a jej środek przesuwa się w dół o
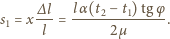
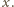 Środek blachy ponownie przesuwa się
w dół na taką samą odległość jak podczas ogrzewania. W ciągu doby blacha
spełza w dół na odległość
Środek blachy ponownie przesuwa się
w dół na taką samą odległość jak podczas ogrzewania. W ciągu doby blacha
spełza w dół na odległość
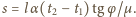
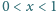 moli gazu
moli gazu
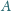 i
i
 moli gazu
moli gazu
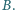 Molowe masy gazów oraz ich
molowe ciepła właściwe w stałej objętości i pod stałym ciśnieniem
wynoszą odpowiednio
Molowe masy gazów oraz ich
molowe ciepła właściwe w stałej objętości i pod stałym ciśnieniem
wynoszą odpowiednio
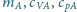 oraz
oraz
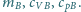 Ile
wynosi prędkość dźwięku
Ile
wynosi prędkość dźwięku
 w tej mieszaninie w temperaturze
w tej mieszaninie w temperaturze
 Uniwersalna stała gazowa wynosi
Uniwersalna stała gazowa wynosi
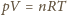 (
(
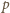 – ciśnienie,
– ciśnienie,
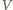 – objętość,
– objętość,
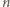 – całkowita liczba moli
gazu), dźwięk rozchodzi się z prędkością daną równaniem
– całkowita liczba moli
gazu), dźwięk rozchodzi się z prędkością daną równaniem
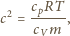
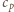 i
i
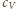 oznaczają ciepła molowe, odpowiednio w stałej
objętości i pod stałym ciśnieniem, a
oznaczają ciepła molowe, odpowiednio w stałej
objętości i pod stałym ciśnieniem, a
 masę jednego mola tego gazu.
Mieszanina gazów doskonałych spełnia równanie gazu doskonałego, masa i
ciepło są tzw. wielkościami ekstensywnymi, a więc odpowiednie wielkości dla
mieszaniny to
masę jednego mola tego gazu.
Mieszanina gazów doskonałych spełnia równanie gazu doskonałego, masa i
ciepło są tzw. wielkościami ekstensywnymi, a więc odpowiednie wielkości dla
mieszaniny to
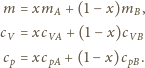
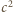 wynosi
wynosi
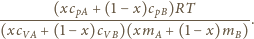
 w azocie).
w azocie).
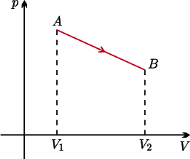
 Końce odcinka
Końce odcinka
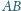 leżą na tej samej izotermie,
a odpowiadające im objętości wynoszą
leżą na tej samej izotermie,
a odpowiadające im objętości wynoszą
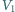 i
i
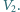 Jaka jest część
odcinka
Jaka jest część
odcinka
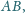 dla której gaz pobiera ciepło w tej przemianie?
dla której gaz pobiera ciepło w tej przemianie?
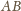 zmienia się liniowo zgodnie ze wzorem
zmienia się liniowo zgodnie ze wzorem
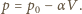 Oznaczając przez
Oznaczając przez
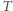 temperaturę w punktach
temperaturę w punktach
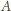 i
i
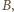 otrzymujemy, korzystając z równania Clapeyrona
otrzymujemy, korzystając z równania Clapeyrona
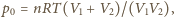
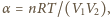 gdzie
gdzie
 oznacza
liczbę moli gazu, a
oznacza
liczbę moli gazu, a
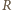 jest stałą gazową. Rozważmy badaną przemianę
w małym przedziale objętości
jest stałą gazową. Rozważmy badaną przemianę
w małym przedziale objętości
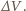 Zgodnie z pierwszą zasadą
termodynamiki ciepło tam przekazane wynosi
Zgodnie z pierwszą zasadą
termodynamiki ciepło tam przekazane wynosi
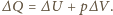 Zmiana
energii wewnętrznej dana jest wzorem
Zmiana
energii wewnętrznej dana jest wzorem
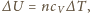 gdzie molowe ciepło
właściwe
gdzie molowe ciepło
właściwe
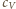 przy stałej objętości dla gazu jednoatomowego
wynosi
przy stałej objętości dla gazu jednoatomowego
wynosi
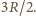 Zmiana temperatury w badanym przedziale wynosi
Zmiana temperatury w badanym przedziale wynosi
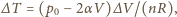 gdzie pominęliśmy wyraz proporcjonalny do
gdzie pominęliśmy wyraz proporcjonalny do
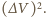 Gaz pobiera ciepło, gdy
Gaz pobiera ciepło, gdy
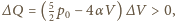 czyli
gdy
czyli
gdy
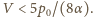 Zatem ciepło w przemianie
Zatem ciepło w przemianie
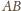 pobierane
jest na odcinku
pobierane
jest na odcinku
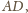 gdzie objętość, odpowiadająca punktowi
gdzie objętość, odpowiadająca punktowi
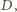 wynosi
wynosi
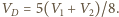
 i
i
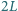 na prawo od
zamkniętego końca znajdują się dwa tłoki, które mogą przemieszczać się bez
tarcia (grubości tłoków pomijamy). W lewej części znajduje się para
wodna pod ciśnieniem
na prawo od
zamkniętego końca znajdują się dwa tłoki, które mogą przemieszczać się bez
tarcia (grubości tłoków pomijamy). W lewej części znajduje się para
wodna pod ciśnieniem
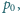 w prawej powietrze o takim samym
ciśnieniu. Ciśnienie pary nasyconej wody w danej temperaturze wynosi
w prawej powietrze o takim samym
ciśnieniu. Ciśnienie pary nasyconej wody w danej temperaturze wynosi
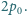 Prawy tłok został wolno wepchnięty na odległość
Prawy tłok został wolno wepchnięty na odległość
 O ile
przesunął się lewy tłok? Temperatura jest stała.
O ile
przesunął się lewy tłok? Temperatura jest stała.
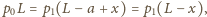 gdzie
gdzie
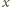 jest
przesunięciem tłoka lewego, zatem
jest
przesunięciem tłoka lewego, zatem
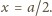 Ciśnienie
Ciśnienie
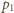 nie
przekracza ciśnienia pary nasyconej:
nie
przekracza ciśnienia pary nasyconej:
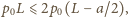 stąd
stąd
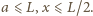
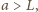 para wodna w lewej komorze zaczyna się skraplać,
ciśnienie ma stałą wartość
para wodna w lewej komorze zaczyna się skraplać,
ciśnienie ma stałą wartość
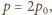 a objętości gazów w obu
częściach są takie same (zaniedbujemy objętość wody powstałej w wyniku
skroplenia w porównaniu z objętością pary nasyconej o tej samej masie).
Oznaczając dodatkowe przesunięcia obu tłoków przez
a objętości gazów w obu
częściach są takie same (zaniedbujemy objętość wody powstałej w wyniku
skroplenia w porównaniu z objętością pary nasyconej o tej samej masie).
Oznaczając dodatkowe przesunięcia obu tłoków przez
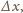 możemy
napisać:
możemy
napisać:
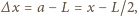 stąd
stąd
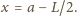 Ostatecznie:
Ostatecznie:
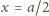 dla
dla
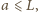
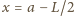 dla
dla
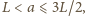
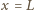 dla
dla
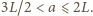
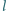 i współczynniku sprężystości
i współczynniku sprężystości
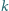 zsuwa się w kierunku pionowym żelazny pierścień o masie
zsuwa się w kierunku pionowym żelazny pierścień o masie
 Siła tarcia między powierzchnią sznura a pierścieniem wynosi
Siła tarcia między powierzchnią sznura a pierścieniem wynosi
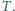 Wyznacz ciepło, które się przy tym wydziela.
Wyznacz ciepło, które się przy tym wydziela.
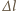 maksymalne wydłużenie sznura. Stwierdzenie, że
pierścień jest żelazny, wskazuje, że masę sznura możemy zaniedbać
w porównaniu z masą pierścienia. Wtedy mamy
maksymalne wydłużenie sznura. Stwierdzenie, że
pierścień jest żelazny, wskazuje, że masę sznura możemy zaniedbać
w porównaniu z masą pierścienia. Wtedy mamy
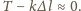 Na
sznur działa siła tarcia, która powoduje jego wydłużenie, czyli
wzrost energii sprężystości oraz wydzielanie się ciepła
Na
sznur działa siła tarcia, która powoduje jego wydłużenie, czyli
wzrost energii sprężystości oraz wydzielanie się ciepła
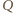 :
:
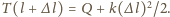 Wiedząc, że
Wiedząc, że
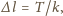 otrzymujemy:
otrzymujemy:
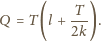
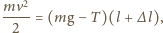 natomiast zasada
zachowania energii dla całego układu sznur–pierścień ma postać:
natomiast zasada
zachowania energii dla całego układu sznur–pierścień ma postać:
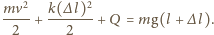 Odejmując te równania stronami,
otrzymujemy taki sam wynik jak poprzednio.
Odejmując te równania stronami,
otrzymujemy taki sam wynik jak poprzednio.
 oraz
oraz
 znajdującymi się na
wysokości
znajdującymi się na
wysokości
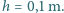 Cylindry połączone są na dole cienką rurką,
wewnątrz nich znajduje się gaz doskonały o stałej temperaturze, a na zewnątrz
jest próżnia. Jaka będzie różnica wysokości tłoków po dociążeniu
pierwszego z nich dodatkowym kilogramem?
Cylindry połączone są na dole cienką rurką,
wewnątrz nich znajduje się gaz doskonały o stałej temperaturze, a na zewnątrz
jest próżnia. Jaka będzie różnica wysokości tłoków po dociążeniu
pierwszego z nich dodatkowym kilogramem?
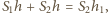 gdzie
gdzie
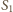 i
i
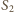 to przekroje wewnętrzne cylindrów, a
to przekroje wewnętrzne cylindrów, a
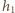 to
wysokość, na którą wzniesie się drugi tłok. Początkowo ciśnienie gazu
w obu naczyniach było jednakowe, tzn.
to
wysokość, na którą wzniesie się drugi tłok. Początkowo ciśnienie gazu
w obu naczyniach było jednakowe, tzn.
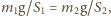 stąd
stąd
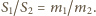 Zatem
Zatem
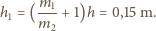
 moli gazu doskonałego poddane jest przemianie cyklicznej
moli gazu doskonałego poddane jest przemianie cyklicznej
 składającej się z dwóch izobar
składającej się z dwóch izobar
 oraz
oraz
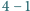 , izochory
, izochory
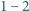 i pewnego procesu
i pewnego procesu
 przedstawionego na wykresie
przedstawionego na wykresie
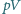 linią prostą. Temperatury gazu
w punktach
linią prostą. Temperatury gazu
w punktach
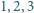 są równe
są równe
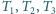 , odpowiednio, a punkty
, odpowiednio, a punkty
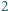 i
i
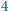 leżą na tej samej izotermie. Wyznaczyć pracę wykonaną
przez gaz.
leżą na tej samej izotermie. Wyznaczyć pracę wykonaną
przez gaz.
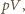 a więc:
a więc:
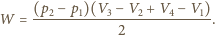
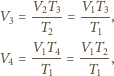
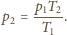
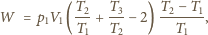
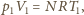 więc ostatecznie
więc ostatecznie
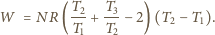
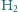 znajduje się w temperaturze 300 K pod ciśnieniem 100 Pa
w naczyniu o stałej objętości. Ile będzie wynosić ciśnienie w naczyniu,
jeśli ogrzać wodór do temperatury
znajduje się w temperaturze 300 K pod ciśnieniem 100 Pa
w naczyniu o stałej objętości. Ile będzie wynosić ciśnienie w naczyniu,
jeśli ogrzać wodór do temperatury
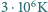 ?
?
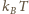 w temperaturze
w temperaturze
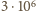 K
wynosi – w przeliczeniu na elektronowolty – około 300 eV, czyli znacznie więcej
zarówno od energii dysocjacji cząsteczek wodoru, jak i energii jonizacji
atomowego wodoru. Każda cząsteczka H
K
wynosi – w przeliczeniu na elektronowolty – około 300 eV, czyli znacznie więcej
zarówno od energii dysocjacji cząsteczek wodoru, jak i energii jonizacji
atomowego wodoru. Każda cząsteczka H
 rozpadnie się więc po
podgrzaniu na cztery cząstki – dwa jądra i dwa elektrony. Ciśnienie wzrośnie
rozpadnie się więc po
podgrzaniu na cztery cząstki – dwa jądra i dwa elektrony. Ciśnienie wzrośnie
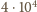 razy i wyniesie 4 MPa.
razy i wyniesie 4 MPa.
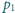 oraz bańka mydlana o promieniu
oraz bańka mydlana o promieniu
 . Napięcie
powierzchniowe błony mydlanej wynosi
. Napięcie
powierzchniowe błony mydlanej wynosi
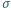 , temperatura układu
, temperatura układu
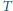 jest utrzymywana na stałym poziomie. Wyznaczyć ciśnienie
jest utrzymywana na stałym poziomie. Wyznaczyć ciśnienie
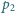 , do
którego należy sprężyć powietrze za pomocą tłoka, żeby promień bańki
zmniejszył się dwukrotnie.
, do
którego należy sprężyć powietrze za pomocą tłoka, żeby promień bańki
zmniejszył się dwukrotnie.
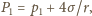 gdzie
gdzie
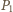 jest ciśnieniem wewnątrz bańki. Po zmniejszeniu promienia bańki
o połowę ciśnienie wywierane przez zakrzywioną powierzchnię bańki
zwiększy się do
jest ciśnieniem wewnątrz bańki. Po zmniejszeniu promienia bańki
o połowę ciśnienie wywierane przez zakrzywioną powierzchnię bańki
zwiększy się do
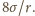 Skoro temperatura układu jest stała, to ciśnienie
powietrza wewnątrz bańki, odwrotnie proporcjonalne do jej objętości,
wzrośnie 8 razy,
Skoro temperatura układu jest stała, to ciśnienie
powietrza wewnątrz bańki, odwrotnie proporcjonalne do jej objętości,
wzrośnie 8 razy,
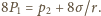 Z otrzymanych dwóch równań
wyznaczamy
Z otrzymanych dwóch równań
wyznaczamy
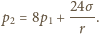
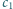 oraz
oraz
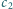 , których temperatury wynoszą, odpowiednio,
, których temperatury wynoszą, odpowiednio,
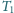 i
i
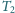 . Po usunięciu przegrody różnica początkowej
temperatury jednej z cieczy oraz ustanowionej temperatury równowagi okazała
się dwa razy mniejsza od początkowej różnicy temperatur cieczy. Znaleźć
stosunek mas cieczy
. Po usunięciu przegrody różnica początkowej
temperatury jednej z cieczy oraz ustanowionej temperatury równowagi okazała
się dwa razy mniejsza od początkowej różnicy temperatur cieczy. Znaleźć
stosunek mas cieczy
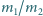 .
.
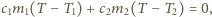 a stąd
a stąd
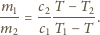
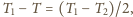 czyli
czyli
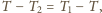 co ostatecznie daje:
co ostatecznie daje:
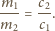
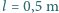 średnia pionowa odległość między atomami wynosi
średnia pionowa odległość między atomami wynosi
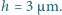
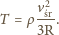
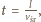 z drugiej jest to czas spadku
swobodnego równy
z drugiej jest to czas spadku
swobodnego równy
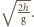 Stąd
Stąd
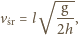
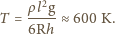
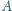 o temperaturze
o temperaturze
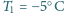 i oddaje ciepło otoczeniu o temperaturze
i oddaje ciepło otoczeniu o temperaturze
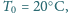 , działając na
następującej zasadzie. Naczynie o stałej objętości początkowo zawiera powietrze
atmosferyczne o temperaturze
, działając na
następującej zasadzie. Naczynie o stałej objętości początkowo zawiera powietrze
atmosferyczne o temperaturze
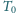 i ciśnieniu
i ciśnieniu
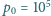 Pa,
następnie przy zachowaniu doskonałej izolacji termicznej pompa próżniowa
obniża ciśnienie w naczyniu do osiągnięcia temperatury
Pa,
następnie przy zachowaniu doskonałej izolacji termicznej pompa próżniowa
obniża ciśnienie w naczyniu do osiągnięcia temperatury
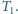 Dalej
odpompowuje się powietrze aż do stanu bliskiego próżni, przy czym
temperatura pozostaje równa
Dalej
odpompowuje się powietrze aż do stanu bliskiego próżni, przy czym
temperatura pozostaje równa
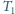 wskutek pobierania ciepła od
wskutek pobierania ciepła od
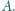 Następnie naczynie jest ponownie napełniane powietrzem atmosferycznym i cykl
się powtarza. Ile wynosi minimalna wartość pracy pompy niezbędnej do
odprowadzenia 1 J ciepła od
Następnie naczynie jest ponownie napełniane powietrzem atmosferycznym i cykl
się powtarza. Ile wynosi minimalna wartość pracy pompy niezbędnej do
odprowadzenia 1 J ciepła od
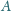 ?
?
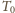 i tłok. Otwarcie zaworu łączącego cylinder z naczyniem następuje
w chwili dojścia tłoka „do końca” (objętość cylindra równa zeru),
po osiągnięciu przez tłok położenia przeciwnego następuje zamknięcie tego
zaworu, a po cofnięciu tłoka do położenia, w którym powietrze pobrane
z naczynia zostanie sprężone do ciśnienia
i tłok. Otwarcie zaworu łączącego cylinder z naczyniem następuje
w chwili dojścia tłoka „do końca” (objętość cylindra równa zeru),
po osiągnięciu przez tłok położenia przeciwnego następuje zamknięcie tego
zaworu, a po cofnięciu tłoka do położenia, w którym powietrze pobrane
z naczynia zostanie sprężone do ciśnienia
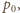 następuje otwarcie
zaworu umożliwiającego odprowadzenie na zewnątrz sprężonej partii gazu.
Ten zawór zostaje zamknięty tuż przed otwarciem pierwszego. Na każdy
cykl przemian w naczyniu próżniowym przypada wiele cykli pracy
pompy. Powietrze należy uważać za gaz doskonały o cieple molowym
następuje otwarcie
zaworu umożliwiającego odprowadzenie na zewnątrz sprężonej partii gazu.
Ten zawór zostaje zamknięty tuż przed otwarciem pierwszego. Na każdy
cykl przemian w naczyniu próżniowym przypada wiele cykli pracy
pompy. Powietrze należy uważać za gaz doskonały o cieple molowym
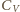 równym (5/2)R.
równym (5/2)R.
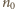 i
i
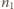 początkową liczbę moli
powietrza w naczyniu oraz liczbę moli w chwili osiągnięcia temperatury
początkową liczbę moli
powietrza w naczyniu oraz liczbę moli w chwili osiągnięcia temperatury
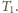 Z równania adiabaty w zmiennych
Z równania adiabaty w zmiennych
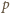 –
–
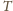
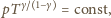
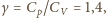 po przekształceniach znajdujemy
po przekształceniach znajdujemy
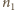

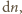 przy założeniu, że ciśnienie w naczyniu
pozostaje w przybliżeniu stałe i równe
przy założeniu, że ciśnienie w naczyniu
pozostaje w przybliżeniu stałe i równe
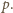 Jeśli objętość
cylindra pompy jest równa
Jeśli objętość
cylindra pompy jest równa
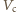 (zgodnie z podanym założeniem
(zgodnie z podanym założeniem
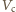 jest znacznie mniejsze od objętości naczynia), to wejdzie do niego
jest znacznie mniejsze od objętości naczynia), to wejdzie do niego
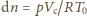 moli powietrza, a praca przeciw sile parcia z zewnątrz
wyniesie
moli powietrza, a praca przeciw sile parcia z zewnątrz
wyniesie
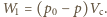 Sprężanie powietrza w cylindrze zachodzi
izotermicznie, zatem praca
Sprężanie powietrza w cylindrze zachodzi
izotermicznie, zatem praca
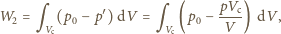
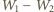 i okazuje się równa
i okazuje się równa
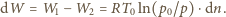
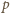 zależy od liczby moli
zależy od liczby moli
 pozostałej w naczyniu wg równania
pozostałej w naczyniu wg równania
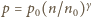 i w wyniku
całkowania otrzymujemy
i w wyniku
całkowania otrzymujemy
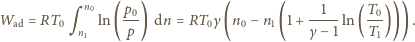
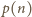 ma postać
ma postać
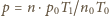 i całkowanie daje wynik
i całkowanie daje wynik
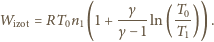
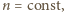
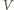 jest
zmienną) ciepło to jest równe
jest
zmienną) ciepło to jest równe
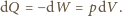
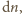 która jest równoważna
która jest równoważna
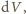 o ile
o ile
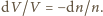 Dlatego
Dlatego
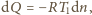 a jeśli stanem
końcowym jest próżnia, to
a jeśli stanem
końcowym jest próżnia, to
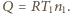 Szukany iloraz
Szukany iloraz
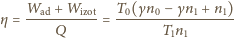
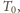
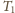 i
i
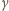 przyjmuje wartość 1,48, co można
porównać z
przyjmuje wartość 1,48, co można
porównać z
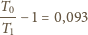
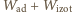 ), to wartość
), to wartość
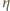 zmalałaby do 0,109.
zmalałaby do 0,109.
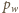 jest równe sumie ciśnienia
zewnętrznego
jest równe sumie ciśnienia
zewnętrznego
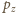 i ciśnienia samej błonki
i ciśnienia samej błonki
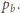 Ciśnienie błonki
jest odwrotnie proporcjonalne do jej promienia, czyli do pierwiastka trzeciego
stopnia z objętości powietrza wewnątrz bańki
Ciśnienie błonki
jest odwrotnie proporcjonalne do jej promienia, czyli do pierwiastka trzeciego
stopnia z objętości powietrza wewnątrz bańki
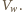 Dla małych
przyrostów mamy więc
Dla małych
przyrostów mamy więc
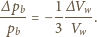
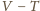 w wersji
różniczkowej ma postać
w wersji
różniczkowej ma postać
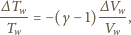
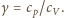 Stąd
Stąd
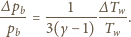
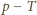 :
:
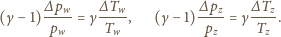
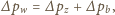 dochodzimy do wyniku
dochodzimy do wyniku