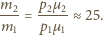Zadania z fizyki - XII 2020»Zadanie 1014
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z fizyki - XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
Szereg promieniotwórczy rozpoczynający się izotopem 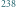 U, o czasie połowicznego rozpadu
U, o czasie połowicznego rozpadu 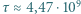 lat, kończy stabilny izotop
lat, kończy stabilny izotop 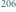 Pb. Jaką objętość
Pb. Jaką objętość 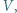 w warunkach normalnych, wypełniłby dzisiaj hel, który powstał w wyniku rozpadu
w warunkach normalnych, wypełniłby dzisiaj hel, który powstał w wyniku rozpadu 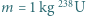 obecnego w chwili powstania Ziemi? Wiek Ziemi oceniany jest na
obecnego w chwili powstania Ziemi? Wiek Ziemi oceniany jest na 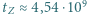 lat.
lat.
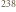 U
U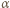
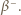
 Pb. Na każdej drodze uwalnianych jest 8 cząstek
Pb. Na każdej drodze uwalnianych jest 8 cząstek 
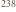 U
U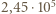
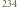 U. Z
U. Z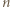
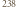 U
U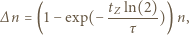
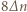
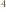 He. W
He. W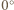 C, ciśnienie 101
C, ciśnienie 101 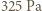 ) hel jest gazem o
) hel jest gazem o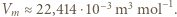
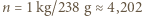
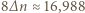
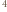 He wypełniłby objętość
He wypełniłby objętość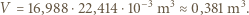
 wymaga dostarczania strumienia energii (ciepła) w ilości
wymaga dostarczania strumienia energii (ciepła) w ilości 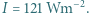 Ile wynosi utrzymywana różnica temperatur
Ile wynosi utrzymywana różnica temperatur 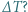 Współczynnik przewodnictwa cieplnego miedzi
Współczynnik przewodnictwa cieplnego miedzi 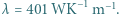 Straty ciepła przez krawędzie boczne płyty pomijamy.
Straty ciepła przez krawędzie boczne płyty pomijamy.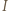 potrzebny do tego, żeby między powierzchniami płyty utrzymywała się stała różnica temperatur
potrzebny do tego, żeby między powierzchniami płyty utrzymywała się stała różnica temperatur 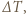 jest proporcjonalny do
jest proporcjonalny do 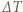 i odwrotnie proporcjonalny do grubości płyty
i odwrotnie proporcjonalny do grubości płyty 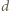 :
: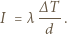
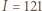 Wm
Wm 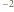 różnica temperatur wynosi więc:
różnica temperatur wynosi więc: 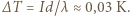
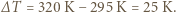 Przy tej samej różnicy temperatur wydajność wymiany ciepła poprzez promieniowanie bardzo szybko rośnie ze wzrostem temperatury - proporcjonalnie do
Przy tej samej różnicy temperatur wydajność wymiany ciepła poprzez promieniowanie bardzo szybko rośnie ze wzrostem temperatury - proporcjonalnie do 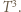
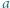 energii promieniowania termicznego padającego na jego powierzchnię. Zgodnie z prawem Kirchhoffa takie ciało emituje ułamek
energii promieniowania termicznego padającego na jego powierzchnię. Zgodnie z prawem Kirchhoffa takie ciało emituje ułamek  energii promieniowanej przez ciało doskonale czarne o równej mu temperaturze. Współczynnik
energii promieniowanej przez ciało doskonale czarne o równej mu temperaturze. Współczynnik 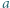 nazywany jest w związku z tym względną zdolnością emisyjną.
nazywany jest w związku z tym względną zdolnością emisyjną.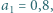 utrzymywana jest w temperaturze
utrzymywana jest w temperaturze 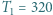 K, a powierzchnia B, o
K, a powierzchnia B, o 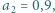 w temperaturze
w temperaturze 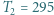 K. Ile wynosi wypadkowy strumień
K. Ile wynosi wypadkowy strumień 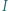 energii promieniowania termicznego przepływającej między tymi powierzchniami? Stała Stefana-Boltzmanna
energii promieniowania termicznego przepływającej między tymi powierzchniami? Stała Stefana-Boltzmanna 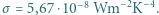 Odległość między powierzchniami jest mała w porównaniu z ich rozmiarami i efekty brzegowe można zaniedbać.
Odległość między powierzchniami jest mała w porównaniu z ich rozmiarami i efekty brzegowe można zaniedbać. energii padającej na jego powierzchnię, to z zasady zachowania energii wynika, że pozostały ułamek
energii padającej na jego powierzchnię, to z zasady zachowania energii wynika, że pozostały ułamek 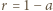 energii jest przez tę powierzchnię odbijany i rozpraszany do otoczenia. Przyjrzyjmy się energii docierającej od ciała A do B. Emitowany przez powierzchnię A strumień energii, równy
energii jest przez tę powierzchnię odbijany i rozpraszany do otoczenia. Przyjrzyjmy się energii docierającej od ciała A do B. Emitowany przez powierzchnię A strumień energii, równy 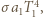 w całości dociera do B. Tam jego część
w całości dociera do B. Tam jego część 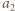 jest przez B absorbowana, a część
jest przez B absorbowana, a część 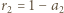 jest rozpraszana (odbijana) i w całości wraca do A (obie powierzchnie traktujemy jak nieskończone płaszczyzny - zaniedbujemy efekty brzegowe), gdzie jej część
jest rozpraszana (odbijana) i w całości wraca do A (obie powierzchnie traktujemy jak nieskończone płaszczyzny - zaniedbujemy efekty brzegowe), gdzie jej część 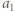 jest absorbowana, a część
jest absorbowana, a część 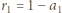 odbijana itd. Od A do B, w wyniku nieskończonej liczby odbić, dociera więc strumień energii:
odbijana itd. Od A do B, w wyniku nieskończonej liczby odbić, dociera więc strumień energii: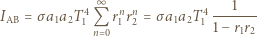
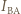 docierającego od B do A, ale z
docierającego od B do A, ale z 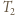 w miejscu
w miejscu 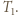 Ostatecznie, poszukiwany strumień
Ostatecznie, poszukiwany strumień 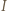 energii netto przepływającej między ciałami wynosi
energii netto przepływającej między ciałami wynosi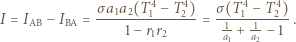
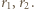 Po podstawieniu danych liczbowych:
Po podstawieniu danych liczbowych: 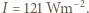
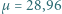 g, przyspieszenie ziemskie
g, przyspieszenie ziemskie 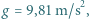 stała gazowa
stała gazowa 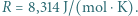 W rozważanych warunkach powietrze spełnia równanie stanu gazu doskonałego.
W rozważanych warunkach powietrze spełnia równanie stanu gazu doskonałego.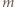 rozszerza się i wznosi pod wpływem siły wyporu, aż osiągnie wysokość
rozszerza się i wznosi pod wpływem siły wyporu, aż osiągnie wysokość 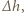 na której jej gęstość zrówna się z gęstością otaczającego gazu. Ze względu na bardzo małe przewodnictwo cieplne wznosząca się "porcja" powietrza podlega przemianie adiabatycznej. Zgodnie z I zasadą termodynamiki zmiana energii wewnętrznej gazu
na której jej gęstość zrówna się z gęstością otaczającego gazu. Ze względu na bardzo małe przewodnictwo cieplne wznosząca się "porcja" powietrza podlega przemianie adiabatycznej. Zgodnie z I zasadą termodynamiki zmiana energii wewnętrznej gazu 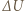 w tej przemianie równa jest pracy sił zewnętrznych działających na gaz:
w tej przemianie równa jest pracy sił zewnętrznych działających na gaz: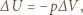
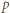 oznacza ciśnienie zewnętrzne, a
oznacza ciśnienie zewnętrzne, a 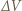 zmianę objętości gazu. Zmiana energii wewnętrznej gazu doskonałego
zmianę objętości gazu. Zmiana energii wewnętrznej gazu doskonałego 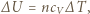 gdzie
gdzie 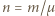 oznacza liczbę moli gazu,
oznacza liczbę moli gazu, 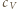 - jego molowe ciepło właściwe w stałej objętości, a
- jego molowe ciepło właściwe w stałej objętości, a 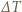 zmianę temperatury. Na podstawie równania stanu gazu doskonałego mamy też:
zmianę temperatury. Na podstawie równania stanu gazu doskonałego mamy też: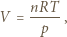
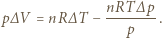
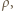 mamy
mamy 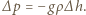 Dostajemy równanie:
Dostajemy równanie: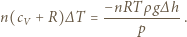
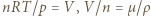 oraz
oraz 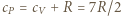 otrzymujemy warunek:
otrzymujemy warunek: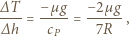
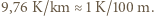
 do
do  , jeżeli temperatura powietrza pozostaje stała i wynosi
, jeżeli temperatura powietrza pozostaje stała i wynosi 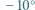 C? Gęstość lodu wynosi
C? Gęstość lodu wynosi 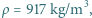 ciepło topnienia
ciepło topnienia 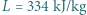 , współczynnik przewodnictwa cieplnego lodu wynosi
, współczynnik przewodnictwa cieplnego lodu wynosi 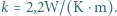
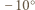 C, natomiast dolna, stykająca się z wodą ma temperaturę
C, natomiast dolna, stykająca się z wodą ma temperaturę 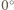 C, równą temperaturze zamarzającej wody. Ciepło przepływa od cieplejszej wody pod powierzchnią lodu do zimniejszego powietrza nad jego powierzchnią i podczas całego procesu różnica temperatur
C, równą temperaturze zamarzającej wody. Ciepło przepływa od cieplejszej wody pod powierzchnią lodu do zimniejszego powietrza nad jego powierzchnią i podczas całego procesu różnica temperatur 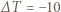 K pozostaje stała, ale rośnie grubość lodu. Powstanie warstwy lodu o grubości
K pozostaje stała, ale rośnie grubość lodu. Powstanie warstwy lodu o grubości 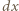 i polu powierzchni
i polu powierzchni 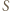 wymaga odebrania ciepła
wymaga odebrania ciepła 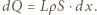 Szybkość przepływu ciepła jest proporcjonalna do powierzchni, różnicy temperatur
Szybkość przepływu ciepła jest proporcjonalna do powierzchni, różnicy temperatur 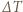 i odwrotnie proporcjonalna do grubości lodu
i odwrotnie proporcjonalna do grubości lodu  (tzn. jest proporcjonalna do szybkości zmian temperatury z grubością) i wynosi:
(tzn. jest proporcjonalna do szybkości zmian temperatury z grubością) i wynosi: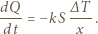
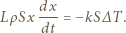
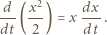
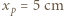 i końcowej
i końcowej 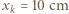 :
: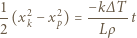
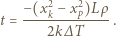
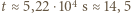 godziny.
godziny.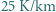 do
do 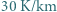 . Oszacuj, jaka byłaby średnia temperatura powierzchni Ziemi, gdyby nie ogrzewało jej Słońce. Dla skał przyjmij średni współczynnik przewodnictwa cieplnego
. Oszacuj, jaka byłaby średnia temperatura powierzchni Ziemi, gdyby nie ogrzewało jej Słońce. Dla skał przyjmij średni współczynnik przewodnictwa cieplnego 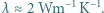 Stała Stefana-Boltzmanna
Stała Stefana-Boltzmanna 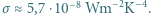
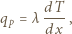
 oznacza głębokość. Strumień energii wypromieniowanej z powierzchni:
oznacza głębokość. Strumień energii wypromieniowanej z powierzchni: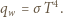
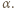 Dla powierzchni Ziemi
Dla powierzchni Ziemi 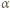 jest bliskie 1, a dla materiałów tworzących skały powierzchniowe mieści się w granicach
jest bliskie 1, a dla materiałów tworzących skały powierzchniowe mieści się w granicach 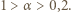
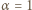 oraz
oraz 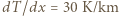 . Równość obu strumieni energii prowadzi do oszacowania:
. Równość obu strumieni energii prowadzi do oszacowania: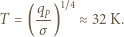
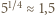 , a więc prowadzi do co najwyżej
, a więc prowadzi do co najwyżej 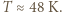
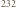 Th o czasie połowicznego rozpadu
Th o czasie połowicznego rozpadu 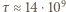 lat,
lat, 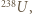
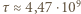 lat oraz
lat oraz 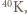
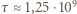 lat.
lat.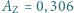 , dla Marsa
, dla Marsa 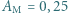 . Strumień energii słonecznej docierającej do Ziemi (stała słoneczna)
. Strumień energii słonecznej docierającej do Ziemi (stała słoneczna) 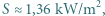 stała Stefana-Boltzmanna
stała Stefana-Boltzmanna 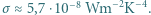 Duża półoś orbity Marsa
Duża półoś orbity Marsa 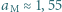 au (
au ( 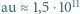 m oznacza tzw. jednostkę astronomiczną równą dużej półosi orbity Ziemi
m oznacza tzw. jednostkę astronomiczną równą dużej półosi orbity Ziemi 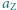 ).
).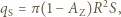
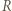 oznacza promień Ziemi. Przyjmując, że Ziemia promieniuje jak ciało doskonale czarne o temperaturze
oznacza promień Ziemi. Przyjmując, że Ziemia promieniuje jak ciało doskonale czarne o temperaturze 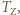 jej powierzchnia wypromieniowuje w jednostce czasu energię równą:
jej powierzchnia wypromieniowuje w jednostce czasu energię równą: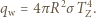
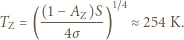
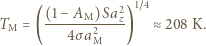
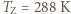 i
i 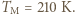 Duża różnica obliczonej i mierzonej temperatury dla Ziemi jest wynikiem istnienia atmosfery (ciśnienie "atmosferyczne" na Marsie wynosi
Duża różnica obliczonej i mierzonej temperatury dla Ziemi jest wynikiem istnienia atmosfery (ciśnienie "atmosferyczne" na Marsie wynosi 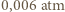 ) i związanego z nią efektu cieplarnianego.
) i związanego z nią efektu cieplarnianego.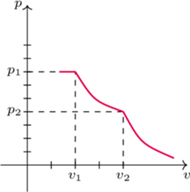
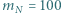
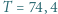
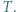
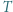
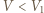
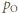
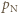
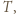
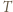
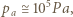
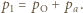
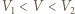
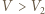
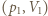
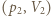
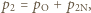
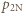
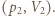
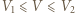
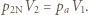
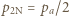
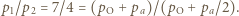
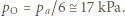
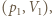
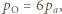
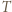
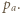
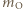
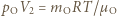
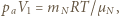
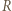
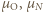
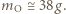
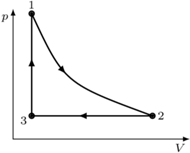
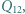 na izobarze wykonana zostaje nad nim praca
na izobarze wykonana zostaje nad nim praca 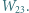 Oblicz sprawność cyklu.
Oblicz sprawność cyklu.
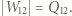 Praca uzyskana w cyklu
Praca uzyskana w cyklu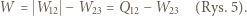
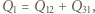 gdzie
gdzie 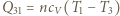 jest ciepłem pobranym na izochorze,
jest ciepłem pobranym na izochorze,  oznacza liczbę moli,
oznacza liczbę moli, 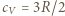 jest molowym ciepłem właściwym przy stałej objętości dla gazu jednoatomowego. Z równania Clapeyrona
jest molowym ciepłem właściwym przy stałej objętości dla gazu jednoatomowego. Z równania Clapeyrona 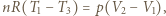 gdzie
gdzie 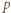 jest ciśnieniem na izobarze,
jest ciśnieniem na izobarze, 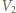 i
i 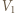 to objętości odpowiednio na początku i końcu tej przemiany. Stąd
to objętości odpowiednio na początku i końcu tej przemiany. Stąd 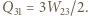
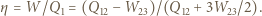
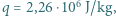 współczynnik napięcia powierzchniowego wody
współczynnik napięcia powierzchniowego wody 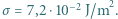 Zakładamy, że temperatura kropli nie zmienia się.
Zakładamy, że temperatura kropli nie zmienia się.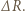 Objętość kropli maleje wtedy o
Objętość kropli maleje wtedy o 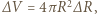 a masa wyparowanej przy tym wody jest równa
a masa wyparowanej przy tym wody jest równa 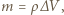 gdzie
gdzie 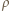 jest gęstością wody. Ciepło potrzebne do wyparowania masy
jest gęstością wody. Ciepło potrzebne do wyparowania masy 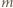 wody wynosi
wody wynosi 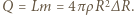 Pole powierzchni kropli maleje o
Pole powierzchni kropli maleje o 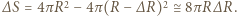 Energia powierzchniowa maleje przy tym o
Energia powierzchniowa maleje przy tym o 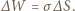 Z bilansu energetycznego
Z bilansu energetycznego 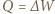 otrzymujemy
otrzymujemy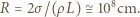
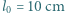 i grubości
i grubości 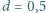
 . Jeden z końców płytki został sztywno zamocowany. O ile przesunie się jej drugi koniec po ogrzaniu płytki o
. Jeden z końców płytki został sztywno zamocowany. O ile przesunie się jej drugi koniec po ogrzaniu płytki o 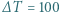 K? Współczynniki rozszerzalności temperaturowej metali wynoszą
K? Współczynniki rozszerzalności temperaturowej metali wynoszą 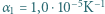 i
i 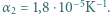 Rozszerzalność temperaturowa oznacza zmianę rozmiarów liniowych ciała według prawa:
Rozszerzalność temperaturowa oznacza zmianę rozmiarów liniowych ciała według prawa: 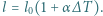
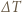 bimetaliczna płytka wygnie się w łuk, a jej zewnętrzne powierzchnie będą łukami o długościach
bimetaliczna płytka wygnie się w łuk, a jej zewnętrzne powierzchnie będą łukami o długościach 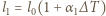 oraz
oraz 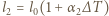 odpowiadającymi kątowi
odpowiadającymi kątowi 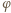 (miara łukowa) i okręgom o promieniach, odpowiednio,
(miara łukowa) i okręgom o promieniach, odpowiednio, 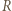 i
i 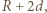 a więc:
a więc: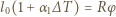
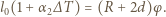
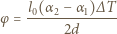
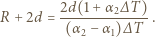
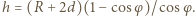 Ostatecznie:
Ostatecznie: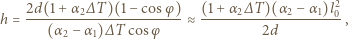
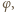 dla otrzymania przybliżonej równości zastosowano przybliżenie
dla otrzymania przybliżonej równości zastosowano przybliżenie 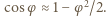 Po podstawieniu danych liczbowych otrzymujemy
Po podstawieniu danych liczbowych otrzymujemy 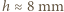 .
.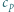 pierwiastków w stanie stałym są w przybliżeniu równe
pierwiastków w stanie stałym są w przybliżeniu równe 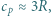 gdzie
gdzie 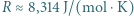 oznacza stałą gazową. Jak można wyjaśnić tę prawidłowość (prawo Dulonga-Petita)? Uogólnij to prawo na przypadek związków chemicznych i na tej podstawie wyznacz przybliżoną wartość molowego ciepła właściwego tlenku żelaza FeO.
oznacza stałą gazową. Jak można wyjaśnić tę prawidłowość (prawo Dulonga-Petita)? Uogólnij to prawo na przypadek związków chemicznych i na tej podstawie wyznacz przybliżoną wartość molowego ciepła właściwego tlenku żelaza FeO.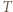 energia drgań każdego z atomów wynosi
energia drgań każdego z atomów wynosi 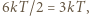 to znaczy: po
to znaczy: po 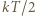 na każdy ze stopni swobody (zmiana energii potencjalnej i kinetycznej drgań w każdym z trzech kierunków przestrzennych;
na każdy ze stopni swobody (zmiana energii potencjalnej i kinetycznej drgań w każdym z trzech kierunków przestrzennych; 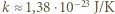 jest stałą Boltzmanna). Takie samo rozumowanie prowadzi do wniosku, że dla związku chemicznego w stanie stałym każdy z atomów też da wkład
jest stałą Boltzmanna). Takie samo rozumowanie prowadzi do wniosku, że dla związku chemicznego w stanie stałym każdy z atomów też da wkład 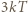 do energii wewnętrznej kryształu. Wniosek: w stanie stałym ciepło molowe związku o
do energii wewnętrznej kryształu. Wniosek: w stanie stałym ciepło molowe związku o 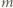 atomach w cząsteczce wynosi w przybliżeniu
atomach w cząsteczce wynosi w przybliżeniu 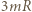 (prawo Koppa-Neumanna). Dla FeO,
(prawo Koppa-Neumanna). Dla FeO, 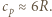
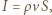 gdzie
gdzie 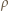 jest gęstością gazu,
jest gęstością gazu,  jest średnią prędkością wypływających cząstek, a
jest średnią prędkością wypływających cząstek, a 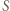 powierzchnią otworu. Na podstawie równania stanu gazu stwierdzamy, że gęstość gazu w pojemniku pod ciśnieniem
powierzchnią otworu. Na podstawie równania stanu gazu stwierdzamy, że gęstość gazu w pojemniku pod ciśnieniem 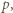 w temperaturze
w temperaturze 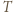 jest proporcjonalna do
jest proporcjonalna do 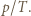 Średnia energia kinetyczna cząsteczek gazu jest proporcjonalna do temperatury
Średnia energia kinetyczna cząsteczek gazu jest proporcjonalna do temperatury 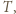 a więc średnia wartość prędkości jest proporcjonalna do
a więc średnia wartość prędkości jest proporcjonalna do 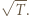 Na tej podstawie stwierdzamy, że:
Na tej podstawie stwierdzamy, że: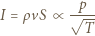
 oznacza proporcjonalność). W warunkach określonych w zadaniu z pierwszego z pojemników tlen ulatnia się więc
oznacza proporcjonalność). W warunkach określonych w zadaniu z pierwszego z pojemników tlen ulatnia się więc 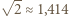 raza szybciej niż z drugiego, mimo że, jak łatwo sprawdzić, początkowo w obu pojemnikach znajdowały się takie same ilości gazu.
raza szybciej niż z drugiego, mimo że, jak łatwo sprawdzić, początkowo w obu pojemnikach znajdowały się takie same ilości gazu.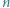 moli jednoatomowego gazu doskonałego. Tłok może przemieszczać się w cylindrze bez tarcia, cylinder i tłok są izolowane cieplnie od otoczenia. Ciśnienie zewnętrzne wynosi
moli jednoatomowego gazu doskonałego. Tłok może przemieszczać się w cylindrze bez tarcia, cylinder i tłok są izolowane cieplnie od otoczenia. Ciśnienie zewnętrzne wynosi 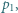 temperatura gazu w cylindrze
temperatura gazu w cylindrze 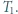 W pewnej chwili ciśnienie zewnętrzne wzrasta skokowo do wartości
W pewnej chwili ciśnienie zewnętrzne wzrasta skokowo do wartości 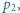 a po ustaleniu się stanu równowagi spada skokowo do pierwotnej wartości. Znaleźć i porównać temperatury gazu w skrajnych stanach równowagi.
a po ustaleniu się stanu równowagi spada skokowo do pierwotnej wartości. Znaleźć i porównać temperatury gazu w skrajnych stanach równowagi.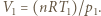 Oznaczmy objętość gazu po zwiększeniu ciśnienia do
Oznaczmy objętość gazu po zwiększeniu ciśnienia do 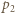 i ustaleniu się równowagi przez
i ustaleniu się równowagi przez 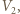 a temperaturę w tym stanie przez
a temperaturę w tym stanie przez 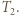 Przemiana jest adiabatyczna, ale nie kwazistacjonarna, korzystamy więc z pierwszej zasady termodynamiki:
Przemiana jest adiabatyczna, ale nie kwazistacjonarna, korzystamy więc z pierwszej zasady termodynamiki: 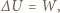 gdzie
gdzie 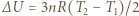 jest zmianą energii wewnętrznej, a praca wykonana nad gazem jest dodatnia i wynosi
jest zmianą energii wewnętrznej, a praca wykonana nad gazem jest dodatnia i wynosi 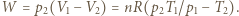 Stąd temperatura w stanie równowagi po sprężeniu gazu wynosi
Stąd temperatura w stanie równowagi po sprężeniu gazu wynosi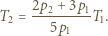
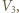 a temperaturę przez
a temperaturę przez 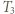 i ponownie korzystając z pierwszej zasady termodynamiki oraz równań Clapeyrona, otrzymujemy równanie:
i ponownie korzystając z pierwszej zasady termodynamiki oraz równań Clapeyrona, otrzymujemy równanie: 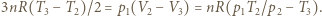 Stąd temperatura w stanie końcowym dana jest wzorem
Stąd temperatura w stanie końcowym dana jest wzorem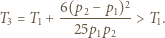
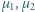 i masach odpowiednio
i masach odpowiednio 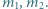 Wewnątrz cylindra znajduje się tłok o masie
Wewnątrz cylindra znajduje się tłok o masie 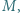 który jest przepuszczalny tylko dla gazu pierwszego. Początkowo tłok znajduje się przy górnej podstawie cylindra, a następnie zostaje puszczony swobodnie. Ile moli gazu pierwszego znajdować się będzie po ustaleniu się równowagi powyżej tłoka? Temperatura układu jest stała i wynosi
który jest przepuszczalny tylko dla gazu pierwszego. Początkowo tłok znajduje się przy górnej podstawie cylindra, a następnie zostaje puszczony swobodnie. Ile moli gazu pierwszego znajdować się będzie po ustaleniu się równowagi powyżej tłoka? Temperatura układu jest stała i wynosi 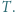 Tarcie tłoka o ścianki można zaniedbać. Wysokość cylindra (nie uwzględniając grubości tłoka) jest równa
Tarcie tłoka o ścianki można zaniedbać. Wysokość cylindra (nie uwzględniając grubości tłoka) jest równa 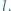
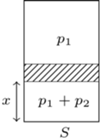
 w obu częściach cylindra jest taka sama, liczba moli gazu pierwszego w jednostce objętości po obu stronach tłoka musi być jednakowa, zatem jednakowe jest też ciśnienie
w obu częściach cylindra jest taka sama, liczba moli gazu pierwszego w jednostce objętości po obu stronach tłoka musi być jednakowa, zatem jednakowe jest też ciśnienie  gazu pierwszego po obu stronach tłoka. Niech
gazu pierwszego po obu stronach tłoka. Niech 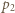 oznacza ciśnienie gazu nieprzenikającego przez tłok w dolnej części cylindra. Warunek równowagi tłoka ma postać
oznacza ciśnienie gazu nieprzenikającego przez tłok w dolnej części cylindra. Warunek równowagi tłoka ma postać 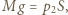 gdzie
gdzie 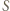 jest polem powierzchni tłoka. Korzystając z równania Clapeyrona dla gazu drugiego, otrzymujemy wyrażenie na odległość
jest polem powierzchni tłoka. Korzystając z równania Clapeyrona dla gazu drugiego, otrzymujemy wyrażenie na odległość 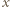 tłoka od dolnej podstawy cylindra:
tłoka od dolnej podstawy cylindra: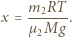
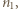 a w dolnej przez
a w dolnej przez 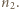 Zachodzi związek
Zachodzi związek 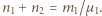 Spełnione są też równania Clapeyrona:
Spełnione są też równania Clapeyrona: 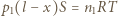 oraz
oraz 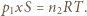 Rozwiązując powyższy układ równań, otrzymujemy szukaną liczbę moli gazu w górnej części naczynia:
Rozwiązując powyższy układ równań, otrzymujemy szukaną liczbę moli gazu w górnej części naczynia: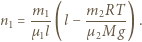
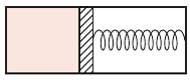
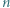 moli jednoatomowego gazu doskonałego, w prawej części jest próżnia. Ile ciepła musi pobrać gaz (np. od umieszczonej w naczyniu spirali grzewczej), aby jego temperatura wzrosła o
moli jednoatomowego gazu doskonałego, w prawej części jest próżnia. Ile ciepła musi pobrać gaz (np. od umieszczonej w naczyniu spirali grzewczej), aby jego temperatura wzrosła o 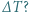 Pojemność cieplną naczynia, tłoka i sprężyny zaniedbujemy.
Pojemność cieplną naczynia, tłoka i sprężyny zaniedbujemy.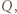 pobrane przez gaz, powoduje przyrost
pobrane przez gaz, powoduje przyrost 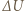 jego energii wewnętrznej oraz zwiększenie energii potencjalnej sprężyny:
jego energii wewnętrznej oraz zwiększenie energii potencjalnej sprężyny: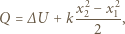
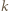 jest współczynnikiem sprężystości, a
jest współczynnikiem sprężystości, a 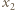 i
i 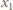 są odkształceniami sprężyny w stanach końcowym i początkowym. Dla gazu jednoatomowego
są odkształceniami sprężyny w stanach końcowym i początkowym. Dla gazu jednoatomowego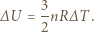
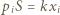 oraz z równań Clapeyrona
oraz z równań Clapeyrona 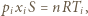 gdzie
gdzie 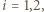 a
a 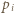 jest ciśnieniem gazu,
jest ciśnieniem gazu, 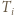 jego temperaturą,
jego temperaturą, 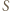 powierzchnią tłoka, otrzymujemy związki
powierzchnią tłoka, otrzymujemy związki 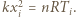 Szukane ciepło wynosi
Szukane ciepło wynosi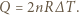
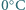 i powtarzał jej pomiar w równych odstępach czasu. Dziesiątemu i jedenastemu pomiarowi odpowiadały odpowiednio temperatury
i powtarzał jej pomiar w równych odstępach czasu. Dziesiątemu i jedenastemu pomiarowi odpowiadały odpowiednio temperatury 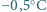 i
i 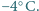 Jaki ułamek masy mokrego śniegu stanowiła woda? Ciepło właściwe lodu
Jaki ułamek masy mokrego śniegu stanowiła woda? Ciepło właściwe lodu  wynosi
wynosi 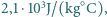 a ciepło topnienia lodu
a ciepło topnienia lodu 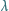 wynosi
wynosi 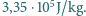
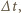 to temperatura śniegu wyniosła
to temperatura śniegu wyniosła 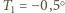 po czasie
po czasie 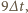 a
a 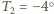 po czasie
po czasie 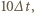 przy czym po czasie
przy czym po czasie 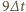 cała zawarta w śniegu woda była już zamarznięta. Zapiszemy bilans cieplny, przyjmując, że prędkość odprowadzania ciepła w zamrażarce jest stała:
cała zawarta w śniegu woda była już zamarznięta. Zapiszemy bilans cieplny, przyjmując, że prędkość odprowadzania ciepła w zamrażarce jest stała: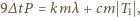
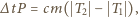
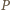 jest energią odprowadzaną w jednostce czasu,
jest energią odprowadzaną w jednostce czasu,  jest masą śniegu, a
jest masą śniegu, a 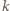 określa ułamek masy wody w śniegu.
określa ułamek masy wody w śniegu.
 która wyparuje w ciągu bardzo małego czasu
która wyparuje w ciągu bardzo małego czasu  przy stałej temperaturze, stałej wilgotności powietrza i braku wiatru, zależy tylko od pola powierzchni wody
przy stałej temperaturze, stałej wilgotności powietrza i braku wiatru, zależy tylko od pola powierzchni wody 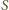 :
: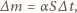
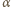 jest współczynnikiem proporcjonalności. Zmiana poziomu wody
jest współczynnikiem proporcjonalności. Zmiana poziomu wody 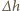 jest związana z
jest związana z 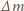 zależnością
zależnością 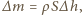 gdzie
gdzie 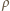 to gęstość wody. Stąd
to gęstość wody. Stąd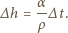
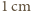 , to całkowicie wyparuje ona z naczynia po 30 dobach.
, to całkowicie wyparuje ona z naczynia po 30 dobach.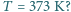 Ciepło parowania wody wynosi
Ciepło parowania wody wynosi 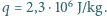
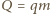 potrzebne do zamiany masy
potrzebne do zamiany masy  wody w parę podczas wrzenia zużywane jest na zwiększenie energii wewnętrznej oraz pracę przeciw siłom zewnętrznego ciśnienia:
wody w parę podczas wrzenia zużywane jest na zwiększenie energii wewnętrznej oraz pracę przeciw siłom zewnętrznego ciśnienia: 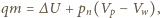 gdzie
gdzie 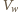 jest objętością wygotowanej wody,
jest objętością wygotowanej wody, 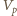 objętością powstałej pary,
objętością powstałej pary, 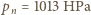 ciśnieniem pary nasyconej wody w temperaturze
ciśnieniem pary nasyconej wody w temperaturze 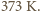 Z równania Clapeyrona
Z równania Clapeyrona 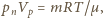 gdzie
gdzie 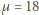 jest masą molową wody. Stosunek gęstości pary nasyconej i wody w temperaturze
jest masą molową wody. Stosunek gęstości pary nasyconej i wody w temperaturze 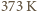 wynosi
wynosi 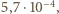 zatem objętość wygotowanej wody możemy pominąć w porównaniu z objętością powstałej pary. Stosunek zmiany energii wewnętrznej do pobranego ciepła dany jest wzorem
zatem objętość wygotowanej wody możemy pominąć w porównaniu z objętością powstałej pary. Stosunek zmiany energii wewnętrznej do pobranego ciepła dany jest wzorem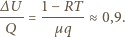
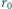 każda, powstała jedna bańka o promieniu
każda, powstała jedna bańka o promieniu 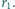 Oszacuj wartość jej promienia. Ciśnienie atmosferyczne wynosi
Oszacuj wartość jej promienia. Ciśnienie atmosferyczne wynosi 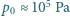 , a dla napięcia powierzchniowego
, a dla napięcia powierzchniowego 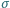 roztworu wody z mydłem przyjmij
roztworu wody z mydłem przyjmij 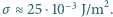
 powoduje, że w jej wnętrzu ciśnienie jest większe od zewnętrznego o
powoduje, że w jej wnętrzu ciśnienie jest większe od zewnętrznego o 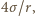 gdzie
gdzie  jest promieniem bańki. Zamknięty w bańce gaz spełnia prawo Boyle'a-Mariotte'a,
jest promieniem bańki. Zamknięty w bańce gaz spełnia prawo Boyle'a-Mariotte'a, 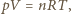 gdzie
gdzie 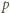 jest ciśnieniem gazu,
jest ciśnieniem gazu, 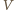 jego objętością,
jego objętością, 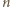 liczbą moli gazu,
liczbą moli gazu, 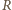 stałą gazową, a
stałą gazową, a 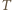 temperaturą w skali bezwzględnej. Oczywiście
temperaturą w skali bezwzględnej. Oczywiście 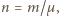 gdzie
gdzie  oznacza masę gazu, a
oznacza masę gazu, a 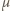 jego masę molową. Masa gazu zamkniętego w bańkach przed i po zderzeniu nie zmienia się, nie zmienia się też temperatura
jego masę molową. Masa gazu zamkniętego w bańkach przed i po zderzeniu nie zmienia się, nie zmienia się też temperatura 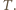 Biorąc to wszystko pod uwagę, otrzymujemy równanie spełniane przez promień
Biorąc to wszystko pod uwagę, otrzymujemy równanie spełniane przez promień 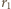 końcowej bańki:
końcowej bańki: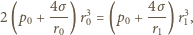
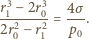
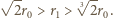
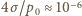 m, to
m, to 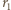 bardzo nieznacznie przewyższa
bardzo nieznacznie przewyższa 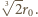

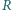 słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja
słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja 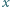 jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi
jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi 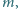 ciśnienie powietrza w piłce
ciśnienie powietrza w piłce 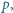 ciśnienie atmosferyczne
ciśnienie atmosferyczne 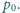

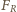 oraz siła
oraz siła 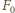 spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc
spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc 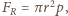 gdzie
gdzie  jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły
jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły 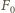 podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni
podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni 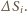 Na każdy element działa prostopadle do niego siła
Na każdy element działa prostopadle do niego siła 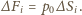 Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła
Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła 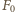 skierowana jest prostopadle w kierunku ściany i ma wartość
skierowana jest prostopadle w kierunku ściany i ma wartość 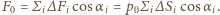 Z
Z 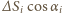 jest rzutem
jest rzutem 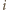 -tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd
-tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd 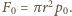 Wypadkowa siła działająca na piłkę wynosi zatem
Wypadkowa siła działająca na piłkę wynosi zatem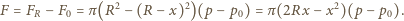
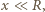 mamy
mamy 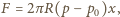 a zwrot
a zwrot 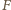 jest przeciwny do deformacji
jest przeciwny do deformacji 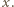 W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem
W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem 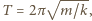 gdzie
gdzie 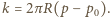 Czas zderzenia piłki ze ścianą równy jest połowie okresu:
Czas zderzenia piłki ze ścianą równy jest połowie okresu: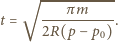

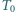 pod ciśnieniem
pod ciśnieniem 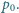 Do wnętrza doprowadzamy pewną ustaloną ilość ciepła
Do wnętrza doprowadzamy pewną ustaloną ilość ciepła 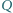 (np. grzałką elektryczną). W którym przypadku ciśnienie wzrośnie bardziej: gdy całe ciepło dostarczymy do jednej części cylindra, czy gdy do każdej części dostarczymy połowę?
(np. grzałką elektryczną). W którym przypadku ciśnienie wzrośnie bardziej: gdy całe ciepło dostarczymy do jednej części cylindra, czy gdy do każdej części dostarczymy połowę?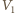 i
i 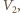 ich temperatury przez
ich temperatury przez 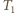 i
i 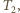 ciśnienie (jednakowe) przez
ciśnienie (jednakowe) przez 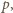 a liczbę moli w każdej z części przez
a liczbę moli w każdej z części przez 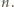 Spełnione są równania
Spełnione są równania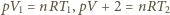
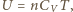 a przyrost całkowitej energii wewnętrznej w każdym z rozpatrywanych przypadków jest równy
a przyrost całkowitej energii wewnętrznej w każdym z rozpatrywanych przypadków jest równy 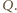 Stąd
Stąd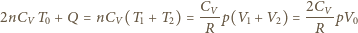
 czyli wzrost ciśnienia nie zależy od tego podziału. (Dość podobne były przed wieloma laty zadania 198 i 257.)
czyli wzrost ciśnienia nie zależy od tego podziału. (Dość podobne były przed wieloma laty zadania 198 i 257.)
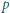 tego gazu w temperaturze
tego gazu w temperaturze 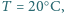 aby izolacja cieplna była skuteczna, jeżeli gazem jest azot, a odległość między podwójnymi ściankami termosu wynosi
aby izolacja cieplna była skuteczna, jeżeli gazem jest azot, a odległość między podwójnymi ściankami termosu wynosi 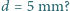 Średnica
Średnica  cząsteczki azotu wynosi około
cząsteczki azotu wynosi około 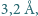 stała Avogadro
stała Avogadro 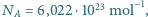 stała gazowa
stała gazowa 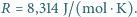
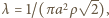 gdzie
gdzie 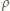 oznacza liczbę cząsteczek gazu w jednostce objętości.
oznacza liczbę cząsteczek gazu w jednostce objętości.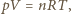 gdzie
gdzie 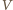 oznacza objętość gazu,
oznacza objętość gazu,  liczbę moli gazu, a
liczbę moli gazu, a 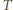 temperaturę w skali Kelvina. Liczba cząsteczek gazu w jednostce objętości
temperaturę w skali Kelvina. Liczba cząsteczek gazu w jednostce objętości 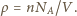 Korzystając z równania stanu oraz warunku
Korzystając z równania stanu oraz warunku 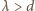 otrzymujemy:
otrzymujemy: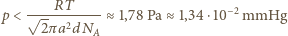
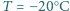 zderzają się. Ile, co najmniej, musiałaby wynosić prędkość każdej z kostek, aby w wyniku tego zderzenia kostki w całości wyparowały? Przyjmij, że w przybliżeniu ciepło właściwe lodu
zderzają się. Ile, co najmniej, musiałaby wynosić prędkość każdej z kostek, aby w wyniku tego zderzenia kostki w całości wyparowały? Przyjmij, że w przybliżeniu ciepło właściwe lodu 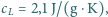 ciepło właściwe wody
ciepło właściwe wody 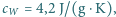 ciepło topnienia lodu
ciepło topnienia lodu 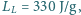 ciepło parowania wody
ciepło parowania wody 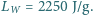
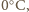 stopnienie lodu, podgrzanie wody do
stopnienie lodu, podgrzanie wody do 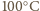 i odparowanie wody:
i odparowanie wody: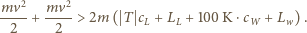
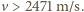

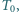 jednakowej w całym naczyniu, objętość gazu nad tłokiem jest
jednakowej w całym naczyniu, objętość gazu nad tłokiem jest 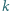 razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości
razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości 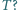
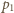 i
i 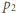 ciśnienia w dolnej i górnej części naczynia w temperaturze
ciśnienia w dolnej i górnej części naczynia w temperaturze 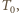 a przez
a przez 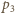 i
i 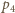 odpowiednie ciśnienia w temperaturze
odpowiednie ciśnienia w temperaturze 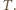 Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury
Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury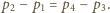
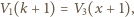
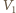 i
i 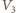 to początkowa i końcowa objętość gazu w dolnej części naczynia, a
to początkowa i końcowa objętość gazu w dolnej części naczynia, a  jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki
jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki 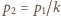 oraz
oraz 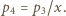 Podstawiając je do równania (1), otrzymujemy
Podstawiając je do równania (1), otrzymujemy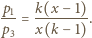
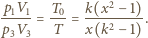
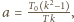 możemy napisać równanie kwadratowe na szukaną wielkość
możemy napisać równanie kwadratowe na szukaną wielkość 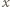 w postaci
w postaci 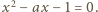 Dodatni pierwiastek tego równania ma postać
Dodatni pierwiastek tego równania ma postać 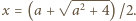 Dla
Dla 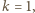 co odpowiada nieważkiemu tłokowi,
co odpowiada nieważkiemu tłokowi, 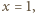 czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego
czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego 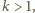 gdy temperatura dąży do nieskończoności, wartość
gdy temperatura dąży do nieskończoności, wartość 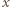 również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.
również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.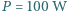 mocy cieplnej. Ile wody musielibyśmy wypocić w ciągu doby, gdyby pocenie było jedynym procesem chłodzenia (tak jest, gdy temperatura otoczenia staje się bliska
mocy cieplnej. Ile wody musielibyśmy wypocić w ciągu doby, gdyby pocenie było jedynym procesem chłodzenia (tak jest, gdy temperatura otoczenia staje się bliska 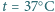 )? Oszacuj, jak dużą powierzchnię
)? Oszacuj, jak dużą powierzchnię 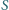 ciała musielibyśmy pozostawić odkrytą w otoczeniu o temperaturze
ciała musielibyśmy pozostawić odkrytą w otoczeniu o temperaturze 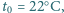 gdyby promieniowanie cieplne było jedynym mechanizmem chłodzenia. Dla uproszczenia zakładamy, że odzież doskonale izoluje cieplnie, a współczynnik promieniowania przez skórę jest bliski 1. Ciepło parowania wody wynosi
gdyby promieniowanie cieplne było jedynym mechanizmem chłodzenia. Dla uproszczenia zakładamy, że odzież doskonale izoluje cieplnie, a współczynnik promieniowania przez skórę jest bliski 1. Ciepło parowania wody wynosi 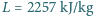 , a stała Boltzmanna to
, a stała Boltzmanna to 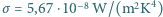 .
.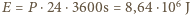 energii. Jest to energia potrzebna do odparowania
energii. Jest to energia potrzebna do odparowania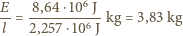
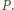 Mamy
Mamy 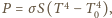 a zatem
a zatem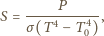
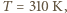 a
a 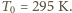
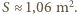 Powierzchnia ciała człowieka dorosłego wynosi średnio niecałe
Powierzchnia ciała człowieka dorosłego wynosi średnio niecałe 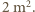 Uwzględnienie faktu, że współczynnik emisji skóry jest mniejszy od 1, zwiększyłoby obliczoną wartość
Uwzględnienie faktu, że współczynnik emisji skóry jest mniejszy od 1, zwiększyłoby obliczoną wartość  Jak z tego widać, w normalnych warunkach pocenie, promieniowanie oraz konwekcja i przewodnictwo cieplne odgrywają istotną rolę.
Jak z tego widać, w normalnych warunkach pocenie, promieniowanie oraz konwekcja i przewodnictwo cieplne odgrywają istotną rolę. i
i 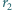 łączą się w jedną bańkę o promieniu
łączą się w jedną bańkę o promieniu 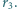 Przyjmując, że napięcie powierzchniowe błonki mydlanej wynosi
Przyjmując, że napięcie powierzchniowe błonki mydlanej wynosi 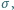 a temperatura
a temperatura 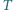 jest jednakowa dla wszystkich rozpatrywanych baniek i równa temperaturze otaczającego powietrza, znaleźć ciśnienie atmosferyczne.
jest jednakowa dla wszystkich rozpatrywanych baniek i równa temperaturze otaczającego powietrza, znaleźć ciśnienie atmosferyczne.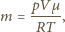
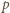 to ciśnienie powietrza w bańce,
to ciśnienie powietrza w bańce, 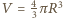 - objętość bańki,
- objętość bańki, 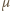 - masa cząsteczkowa powietrza.
- masa cząsteczkowa powietrza.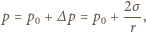
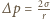 to dodatkowe ciśnienie pod sferyczną powierzchnią błonki o niewielkim promieniu
to dodatkowe ciśnienie pod sferyczną powierzchnią błonki o niewielkim promieniu 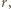 a
a 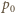 to ciśnienie atmosferyczne.
to ciśnienie atmosferyczne.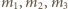 mamy
mamy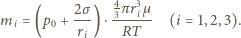
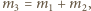 dostajemy ostatecznie
dostajemy ostatecznie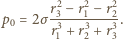
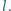 Po obciążeniu tłoka ciężarkiem o masie
Po obciążeniu tłoka ciężarkiem o masie  i ustaleniu się równowagi temperatura bezwzględna gazu wzrosła dwukrotnie. Cylinder i tłok wykonane są z izolatora cieplnego. Obliczyć przyrost energii wewnętrznej gazu. Pominąć tarcie między cylindrem a tłokiem.
i ustaleniu się równowagi temperatura bezwzględna gazu wzrosła dwukrotnie. Cylinder i tłok wykonane są z izolatora cieplnego. Obliczyć przyrost energii wewnętrznej gazu. Pominąć tarcie między cylindrem a tłokiem.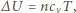 gdzie
gdzie 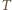 jest temperaturą w stanie początkowym,
jest temperaturą w stanie początkowym, 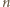 liczbą moli, a
liczbą moli, a 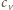 molowym ciepłem właściwym przy stałej objętości. Oznaczmy ciśnienia początkowe i końcowe w cylindrze odpowiednio przez
molowym ciepłem właściwym przy stałej objętości. Oznaczmy ciśnienia początkowe i końcowe w cylindrze odpowiednio przez 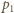 i
i 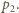 Równania Clapeyrona dla tych stanów mają postać:
Równania Clapeyrona dla tych stanów mają postać: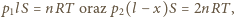
 jest przesunięciem tłoka, a
jest przesunięciem tłoka, a 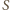 jego polem powierzchni. Odejmując te równania stronami, otrzymujemy
jego polem powierzchni. Odejmując te równania stronami, otrzymujemy 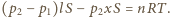 Z warunków równowagi mamy
Z warunków równowagi mamy 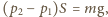 a z pierwszej zasady termodynamiki
a z pierwszej zasady termodynamiki 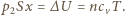 Stąd
Stąd 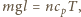 uwzględniając, że
uwzględniając, że 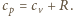 Szukana zmiana energii wewnętrznej wynosi
Szukana zmiana energii wewnętrznej wynosi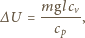
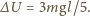
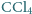 i woda. Pod ciśnieniem normalnym
i woda. Pod ciśnieniem normalnym 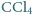 wrze w temperaturze
wrze w temperaturze 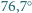 C. W wyniku równomiernego ogrzewania szklanki w kąpieli wodnej, w temperaturze
C. W wyniku równomiernego ogrzewania szklanki w kąpieli wodnej, w temperaturze 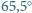 rozpoczyna się wrzenie na granicy rozdziału cieczy. Jaki jest stosunek mas czterochlorku węgla i wody, które wykipią w określonym czasie przy takim "granicznym" wrzeniu? Ciśnienie pary nasyconej wody w temperaturze
rozpoczyna się wrzenie na granicy rozdziału cieczy. Jaki jest stosunek mas czterochlorku węgla i wody, które wykipią w określonym czasie przy takim "granicznym" wrzeniu? Ciśnienie pary nasyconej wody w temperaturze 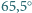 wynosi
wynosi 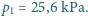
 znajduje się nasycona para wodna oraz nasycona para czterochlorku węgla, przy czym suma ich ciśnień cząstkowych równa jest ciśnieniu atmosferycznemu
znajduje się nasycona para wodna oraz nasycona para czterochlorku węgla, przy czym suma ich ciśnień cząstkowych równa jest ciśnieniu atmosferycznemu 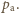 Stąd ciśnienie pary nasyconej CCl
Stąd ciśnienie pary nasyconej CCl  wynosi
wynosi 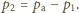 W czasie wrzenia pęcherzyki unoszą się w górę, dochodzą do powierzchni cieczy i pękają. Zatem stosunek mas czterochlorku węgla i wody, które wyparują w określonym czasie, równy jest stosunkowi gęstości par tych substancji
W czasie wrzenia pęcherzyki unoszą się w górę, dochodzą do powierzchni cieczy i pękają. Zatem stosunek mas czterochlorku węgla i wody, które wyparują w określonym czasie, równy jest stosunkowi gęstości par tych substancji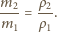
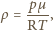
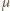 jest masą molową substancji, otrzymujemy:
jest masą molową substancji, otrzymujemy: