Klub 44F - zadania X 2011»Zadanie 525
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania X 2011
- Publikacja w Delcie: październik 2011
- Publikacja elektroniczna: 2 października 2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (64 KB)
Do naczynia nalano słonej wody, a na wierzch – wody czystej, tak że
wysokość słupa wody wynosi
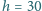 cm, a gęstość zmienia
się liniowo z wysokością od
cm, a gęstość zmienia
się liniowo z wysokością od
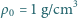 przy powierzchni do
przy powierzchni do
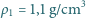 przy dnie. W połowie głębokości naczynia pływa
w stanie równowagi nurek Kartezjusza – niewielka probówka ze szkła
o gęstości
przy dnie. W połowie głębokości naczynia pływa
w stanie równowagi nurek Kartezjusza – niewielka probówka ze szkła
o gęstości
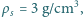 zawierająca pewną ilość powietrza
i otwarta od dołu. Czy ten stan równowagi jest trwały ze względu na
małe przesunięcia pionowe nurka? Ciśnienie atmosferyczne wynosi
zawierająca pewną ilość powietrza
i otwarta od dołu. Czy ten stan równowagi jest trwały ze względu na
małe przesunięcia pionowe nurka? Ciśnienie atmosferyczne wynosi
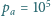 Pa.
Pa.
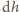 w górę powoduje spadek
siły wyporu o wielkość
w górę powoduje spadek
siły wyporu o wielkość
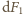 wynikającą ze spadku gęstości
wody
wynikającą ze spadku gęstości
wody
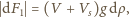
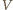 jest objętością powietrza w nurku,
jest objętością powietrza w nurku,
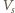 – objętością
szkła, a
– objętością
szkła, a
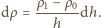 Z drugiej strony, nastąpi wtedy wzrost siły
wyporu o wielkość
Z drugiej strony, nastąpi wtedy wzrost siły
wyporu o wielkość
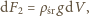
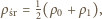 a
a
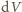 jest wzrostem objętości, będącym
skutkiem spadku ciśnienia i rozprężenia powietrza w nurku. Warunkiem
równowagi trwałej jest
jest wzrostem objętości, będącym
skutkiem spadku ciśnienia i rozprężenia powietrza w nurku. Warunkiem
równowagi trwałej jest
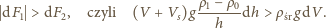
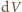 na podstawie prawa przemiany izotermicznej, gdyż
powietrza w nurku jest niewiele i kontakt ze ściankami zapewnia stałość
temperatury. Zatem
na podstawie prawa przemiany izotermicznej, gdyż
powietrza w nurku jest niewiele i kontakt ze ściankami zapewnia stałość
temperatury. Zatem
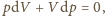 albo
albo
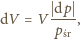
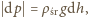 a
a
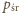 jest ciśnieniem w położeniu
równowagi nurka, czyli sumą ciśnienia atmosferycznego i ciśnienia górnej
połowy słupa wody. Średnia gęstość wody w górnej połowie wynosi
jest ciśnieniem w położeniu
równowagi nurka, czyli sumą ciśnienia atmosferycznego i ciśnienia górnej
połowy słupa wody. Średnia gęstość wody w górnej połowie wynosi
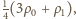 zatem
zatem
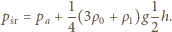
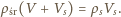
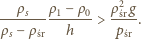
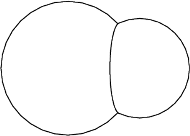
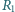 i
i
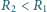 są
połączone tak, jak na rysunku. Jaki promień krzywizny ma błonka oddzielająca
bańki?
są
połączone tak, jak na rysunku. Jaki promień krzywizny ma błonka oddzielająca
bańki?
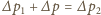 , czyli
, czyli
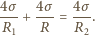
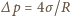 , ponieważ błonka ma dwie powierzchnie: zewnętrzną
i wewnętrzną. Zatem
, ponieważ błonka ma dwie powierzchnie: zewnętrzną
i wewnętrzną. Zatem
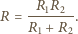
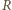 . Powierzchnia tego koła wynosi
. Powierzchnia tego koła wynosi
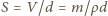 . Siła przyciągania między płytkami równa jest
. Siła przyciągania między płytkami równa jest
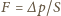 , gdzie
, gdzie
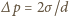 jest ciśnieniem wywieranym przez
zakrzywioną powierzchnię cieczy. Ostatecznie
jest ciśnieniem wywieranym przez
zakrzywioną powierzchnię cieczy. Ostatecznie
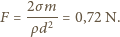
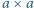
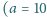 cm) i długości
cm) i długości
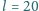 cm. Jaka
ilość ciepła wydzieli się w wyniku przewrócenia się tego klocka?
Przyjmujemy, że gęstość drewna jest równa połowie gęstości wody.
cm. Jaka
ilość ciepła wydzieli się w wyniku przewrócenia się tego klocka?
Przyjmujemy, że gęstość drewna jest równa połowie gęstości wody.
 masę wody wypieranej przez klocek. Gdy jest on
zanurzony pionowo, środek ciężkości zanurzonej części jest na głębokości
masę wody wypieranej przez klocek. Gdy jest on
zanurzony pionowo, środek ciężkości zanurzonej części jest na głębokości
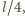 gdy poziomo, na głębokości
gdy poziomo, na głębokości
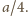 A więc położenie środka
ciężkości klocka po przewróceniu podniesie się o
A więc położenie środka
ciężkości klocka po przewróceniu podniesie się o
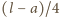 i o tyle
obniży się środek ciężkości wypartej wody. Zatem energia potencjalna wody
w naczyniu spadnie, a energia potencjalna całego klocka nie zmieni się.
Wydzielone ciepło będzie więc równe
i o tyle
obniży się środek ciężkości wypartej wody. Zatem energia potencjalna wody
w naczyniu spadnie, a energia potencjalna całego klocka nie zmieni się.
Wydzielone ciepło będzie więc równe
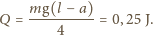
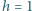 m
i jednego segmentu dłuższego. Jeśli początkowo rurka nie zawierała wody, to
do jakiej wysokości należy jej nalać do dłuższego segmentu, żeby zaczęła
wyciekać drugim końcem? Średnica rurki jest znacznie mniejsza od
m
i jednego segmentu dłuższego. Jeśli początkowo rurka nie zawierała wody, to
do jakiej wysokości należy jej nalać do dłuższego segmentu, żeby zaczęła
wyciekać drugim końcem? Średnica rurki jest znacznie mniejsza od
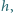 ale na tyle duża, że przepływ wody i przepływ powietrza mogą w niej
zachodzić niezależnie. Temperatura powietrza w rurce się nie zmienia,
a ciśnienie atmosferyczne wynosi
ale na tyle duża, że przepływ wody i przepływ powietrza mogą w niej
zachodzić niezależnie. Temperatura powietrza w rurce się nie zmienia,
a ciśnienie atmosferyczne wynosi
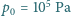 .
.
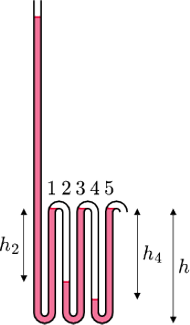
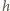 (pomijamy objętość samego kolanka); później sytuacja się powtarza
w segmencie 4. Wzrost poziomu wody w segmentach 3 i 5 powoduje
sprężenie tych słupów powietrza – oznaczmy długości słupów po sprężeniu
jako
(pomijamy objętość samego kolanka); później sytuacja się powtarza
w segmencie 4. Wzrost poziomu wody w segmentach 3 i 5 powoduje
sprężenie tych słupów powietrza – oznaczmy długości słupów po sprężeniu
jako
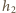 i
i
 Zatem ciśnienie powietrza w segmencie 4 jest
równe
Zatem ciśnienie powietrza w segmencie 4 jest
równe
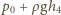 (gdzie
(gdzie
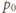 – ciśnienie atmosferyczne),
a w segmencie 2 równe
– ciśnienie atmosferyczne),
a w segmencie 2 równe
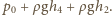 Zgodnie z równaniem
przemiany izotermicznej
Zgodnie z równaniem
przemiany izotermicznej
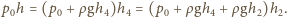
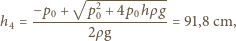
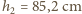 .
.
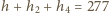 cm (177 cm powyżej górnych kolanek).
cm (177 cm powyżej górnych kolanek).

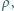 w opisanej
sytuacji pozostaje on w równowadze, a jego nacisk na dno naczynia jest równy
połowie jego ciężaru, to ile wynosi gęstość cieczy z lewej strony walca, a ile –
z prawej?
w opisanej
sytuacji pozostaje on w równowadze, a jego nacisk na dno naczynia jest równy
połowie jego ciężaru, to ile wynosi gęstość cieczy z lewej strony walca, a ile –
z prawej?

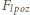 wywieranej na walec od lewej strony można
obliczyć tak, jakby działała na ściankę pionową. Ponieważ ciśnienie
zmienia się proporcjonalnie do głębokości, więc powierzchnię ścianki
wywieranej na walec od lewej strony można
obliczyć tak, jakby działała na ściankę pionową. Ponieważ ciśnienie
zmienia się proporcjonalnie do głębokości, więc powierzchnię ścianki
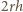 pomnożymy przez ciśnienie w połowie głębokości, równe
pomnożymy przez ciśnienie w połowie głębokości, równe
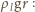
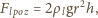
 – promień walca,
– promień walca,
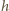 – jego wysokość (tu długość),
– jego wysokość (tu długość),
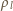 – gęstość cieczy z lewej strony. Podobny argument zastosowany do
ćwiartki walca pozwala obliczyć poziomą składową siły wywieranej na walec
od prawej strony
– gęstość cieczy z lewej strony. Podobny argument zastosowany do
ćwiartki walca pozwala obliczyć poziomą składową siły wywieranej na walec
od prawej strony
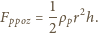
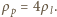
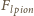 siły działającej z lewej strony,
rozważmy walec zanurzony obustronnie w jednakowej cieczy. Siła wyporu
równa jest ciężarowi wypartej cieczy, a z drugiej strony jest ona równa
siły działającej z lewej strony,
rozważmy walec zanurzony obustronnie w jednakowej cieczy. Siła wyporu
równa jest ciężarowi wypartej cieczy, a z drugiej strony jest ona równa
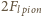 (z symetrii). Stąd
(z symetrii). Stąd
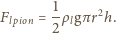
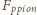 należy analogicznie rozpatrzyć siłę wyporu
działającą na dolną połówkę walca. Wynikiem jest
należy analogicznie rozpatrzyć siłę wyporu
działającą na dolną połówkę walca. Wynikiem jest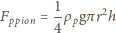
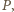 to
to
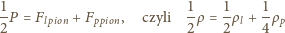
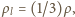
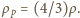
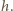 W położeniu równowagi
masa butelki
W położeniu równowagi
masa butelki
 równa jest masie wypartej wody
równa jest masie wypartej wody
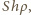 gdzie
gdzie
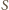 – pole przekroju poprzecznego butelki,
– pole przekroju poprzecznego butelki,
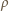 – gęstość wody.
Jeśli zanurzenie zwiększy się o
– gęstość wody.
Jeśli zanurzenie zwiększy się o
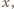 to siła wyporu wzrośnie o
to siła wyporu wzrośnie o
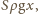 zatem mamy do czynienia z ruchem harmonicznym o okresie
zatem mamy do czynienia z ruchem harmonicznym o okresie
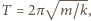 gdzie
gdzie
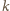 – stała proporcjonalności siły do
wychylenia, tzn.
– stała proporcjonalności siły do
wychylenia, tzn.
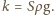 Po przekształceniach można wyznaczyć
Po przekształceniach można wyznaczyć
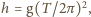 tą drogą Fizyk otrzymał wynik
tą drogą Fizyk otrzymał wynik
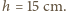
 we wzorze na
we wzorze na
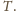 W efekcie
wyliczona wartość
W efekcie
wyliczona wartość
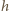 będzie zawyżona – w przeprowadzonym
doświadczeniu autor otrzymał zanurzenie o około 25% mniejsze, co
w opisanej sytuacji odpowiadałoby wartości
będzie zawyżona – w przeprowadzonym
doświadczeniu autor otrzymał zanurzenie o około 25% mniejsze, co
w opisanej sytuacji odpowiadałoby wartości
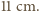 A jednak wygrał
Humanista...
A jednak wygrał
Humanista...
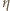 zdefiniowany wzorem
zdefiniowany wzorem
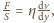 gdzie
gdzie
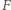 – siła działająca stycznie na
powierzchnię cieczy
– siła działająca stycznie na
powierzchnię cieczy
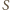 , wzdłuż której następuje poślizg warstw,
, wzdłuż której następuje poślizg warstw,
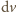 – różnica prędkości warstw na odcinku
– różnica prędkości warstw na odcinku
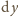 prostopadłym
do
prostopadłym
do
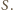
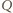 (wyrażony w m
(wyrażony w m
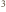 /s), są: średnica rurki
/s), są: średnica rurki
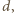 jej
długość
jej
długość
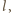 różnica ciśnień
różnica ciśnień
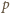 i lepkość
i lepkość
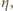 której
jednostką w układzie SI jest
której
jednostką w układzie SI jest
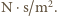 Parametry
Parametry
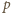 i
i
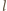 muszą
wystąpić w postaci ilorazu
muszą
wystąpić w postaci ilorazu
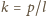 o wymiarze
o wymiarze
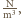 który jest
„czynnikiem napędowym” przepływu. Zatem
który jest
„czynnikiem napędowym” przepływu. Zatem
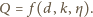
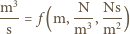
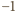 (zależność ta jest znana jako
wzór Hagena–Poiseuille’a). Po dwukrotnym powiększeniu średnicy rurki
przepływ wzrośnie 16-krotnie.
(zależność ta jest znana jako
wzór Hagena–Poiseuille’a). Po dwukrotnym powiększeniu średnicy rurki
przepływ wzrośnie 16-krotnie.