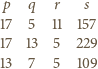Przyjmijmy oznaczenia: 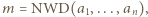
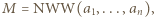
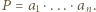 Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn
Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn 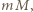 wchodzi do iloczynu
wchodzi do iloczynu 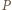 w co najmniej takiej samej potędze. Niech więc
w co najmniej takiej samej potędze. Niech więc 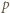 będzie liczbą pierwszą i niech (dla
będzie liczbą pierwszą i niech (dla 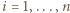 )
) 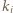 będzie takim wykładnikiem, że
będzie takim wykładnikiem, że 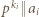 (ten napis oznacza, że
(ten napis oznacza, że 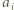 dzieli się przez
dzieli się przez 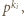 ale nie przez
ale nie przez 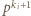 ). Wówczas
). Wówczas 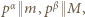 gdzie
gdzie 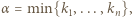
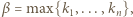 i wobec tego
i wobec tego 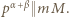 Oczywiście
Oczywiście 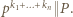 Porównanie wykładników nie pozostawia wątpliwości:
Porównanie wykładników nie pozostawia wątpliwości:
 |
(1) |
Wobec dowolności wyboru 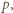 uzasadnia to zadaną nierówność
uzasadnia to zadaną nierówność 
Kiedy zachodzi równość 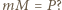 Wtedy, gdy każda liczba pierwsza dzieli
Wtedy, gdy każda liczba pierwsza dzieli 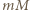 w dokładnie tej samej potędze, w jakiej dzieli
w dokładnie tej samej potędze, w jakiej dzieli 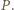 Czyli gdy dla każdej liczby pierwszej
Czyli gdy dla każdej liczby pierwszej 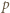 nierówność (1) (z wykładnikami
nierówność (1) (z wykładnikami 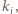 wyznaczonymi przez
wyznaczonymi przez 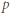 ) staje się równością.
) staje się równością.
Dla 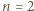 jest tak zawsze; dostajemy znaną tożsamość:
jest tak zawsze; dostajemy znaną tożsamość: 
Dla 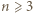 równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb
równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb 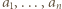 może dzielić się przez
może dzielić się przez 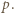 Wobec dowolności
Wobec dowolności 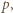 znaczy to, że liczby
znaczy to, że liczby 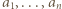 są parami względnie pierwsze.
są parami względnie pierwsze.
I na odwrót, gdy tak jest, wówczas dla każdej liczby pierwszej 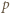 mamy w ciągu
mamy w ciągu 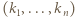 co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji
co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji 
Podsumowując: dla 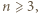 równość
równość 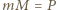 zachodzi wtedy i tylko wtedy, gdy liczby
zachodzi wtedy i tylko wtedy, gdy liczby 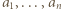 są parami względnie pierwsze; dla
są parami względnie pierwsze; dla 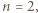 ta równość jest tożsamością.
ta równość jest tożsamością.
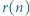 sumę
sumę  liczb będących resztami z dzielenia dodatniej liczby całkowitej
liczb będących resztami z dzielenia dodatniej liczby całkowitej 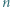 przez
przez 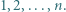 Udowodnij, że istnieje nieskończenie wiele takich
Udowodnij, że istnieje nieskończenie wiele takich 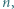 że
że 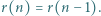
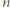 przez liczbę
przez liczbę 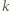 jest równa
jest równa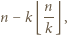
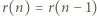 można przepisać jako
można przepisać jako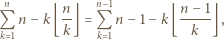
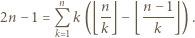
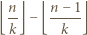
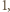 jeżeli
jeżeli 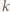 dzieli
dzieli  oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako
oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako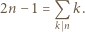
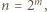 gdzie
gdzie 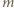 jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb
jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb  spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.
spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.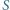 oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.
oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.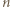 jest liczbą podzielną przez
jest liczbą podzielną przez 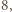 to
to  nie można zapisać w postaci sumy dwóch elementów zbioru
nie można zapisać w postaci sumy dwóch elementów zbioru 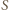 albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru
albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru 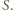 Przypuśćmy, że
Przypuśćmy, że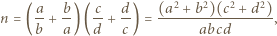
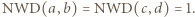 Skoro
Skoro 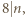 to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez
to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez 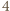 ; bez straty ogólności załóżmy, że
; bez straty ogólności załóżmy, że 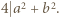 Stąd wynika, że liczby
Stąd wynika, że liczby 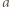 i
i 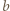 są tej samej parzystości, skąd wobec
są tej samej parzystości, skąd wobec 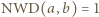 - obie są nieparzyste. Jednak wówczas
- obie są nieparzyste. Jednak wówczas 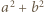 daje resztę
daje resztę 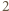 przy dzieleniu przez
przy dzieleniu przez 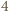 - sprzeczność.
- sprzeczność.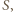 rozważymy ciąg Fibonacciego
rozważymy ciąg Fibonacciego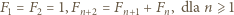
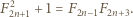
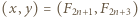 mamy więc
mamy więc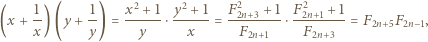
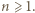 To kończy dowód, gdyż dla różnych
To kończy dowód, gdyż dla różnych 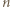 otrzymujemy różne liczby.
otrzymujemy różne liczby.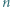 będzie dodatnią liczbą całkowitą. Wykazać, że
będzie dodatnią liczbą całkowitą. Wykazać, że 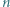 jest sumą dwóch elementów zbioru
jest sumą dwóch elementów zbioru 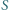 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 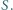
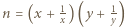 dla pewnych
dla pewnych 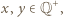 to
to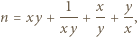
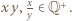 To dowodzi, że jeżeli
To dowodzi, że jeżeli 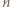 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 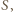 to jest również sumą dwóch elementów zbioru
to jest również sumą dwóch elementów zbioru 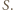
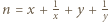 dla pewnych
dla pewnych 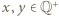 oraz niech
oraz niech 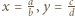 będą zapisami liczb
będą zapisami liczb 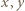 w postaci ułamków nieskracalnych, czyli
w postaci ułamków nieskracalnych, czyli 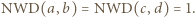 Wówczas
Wówczas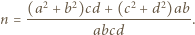
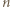 jest liczbą całkowitą, więc
jest liczbą całkowitą, więc 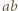 musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że
musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że 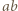 dzieli
dzieli 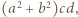 skąd wobec
skąd wobec 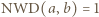 mamy, że
mamy, że 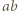 dzieli
dzieli 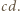 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że 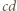 dzieli
dzieli 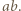 Zatem
Zatem 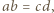 czyli
czyli 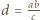 i w konsekwencji
i w konsekwencji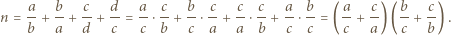
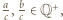 to
to 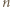 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 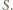
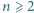 wyznaczyć taki wielomian
wyznaczyć taki wielomian 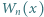 o współczynnikach wymiernych, że
o współczynnikach wymiernych, że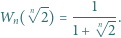
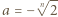 oraz
oraz 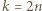 do tożsamości
do tożsamości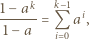
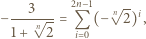
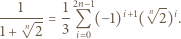
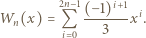
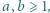 względnie pierwsze i takie, że wzór rekurencyjny
względnie pierwsze i takie, że wzór rekurencyjny
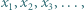 którego wszystkie wyrazy są liczbami złożonymi?
którego wszystkie wyrazy są liczbami złożonymi?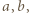 o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek):
o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek): 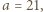
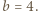 Wówczas
Wówczas 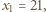
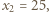 i dalej (dla każdego
i dalej (dla każdego 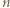 ):
):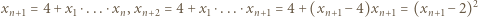
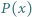 stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna
stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna 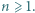 Udowodnić, że może istnieć co najwyżej jeden wielomian
Udowodnić, że może istnieć co najwyżej jeden wielomian 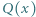 stopnia
stopnia 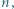 spełniający równanie
spełniający równanie 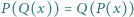 dla
dla 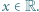
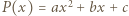
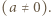 Przypuśćmy, że dla ustalonej liczby
Przypuśćmy, że dla ustalonej liczby 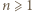 istnieją dwa różne wielomiany
istnieją dwa różne wielomiany 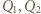 stopnia
stopnia 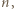 spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez
spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez 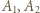 (więc
(więc 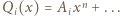 );
); 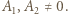 Przyrównując współczynniki wiodące po obu stronach równania
Przyrównując współczynniki wiodące po obu stronach równania 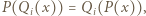 widzimy, że
widzimy, że 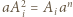 (dla
(dla 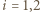 ). Zatem
). Zatem 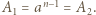 Stąd wynika, że różnica
Stąd wynika, że różnica 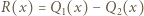 jest niezerowym wielomianem stopnia
jest niezerowym wielomianem stopnia 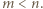
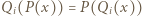 (dla
(dla 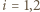 ) i przekształcamy uzyskaną równość:
) i przekształcamy uzyskaną równość: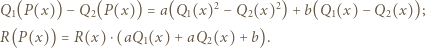
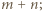 wielomian po lewej stronie ma stopień
wielomian po lewej stronie ma stopień 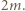 To już sprzeczność, skoro
To już sprzeczność, skoro 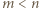 ; dwa różne wielomiany
; dwa różne wielomiany 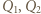 stopnia
stopnia 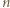 o podanej własności istnieć nie mogą.
o podanej własności istnieć nie mogą.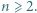
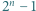 jest bezkwadratowa, to liczby
jest bezkwadratowa, to liczby 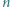 oraz
oraz 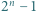 są względnie pierwsze.
są względnie pierwsze. oraz
oraz 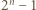 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 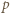 (jasne, że
(jasne, że 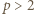 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 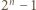 dzieli się przez
dzieli się przez 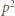 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 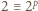 (mod
(mod 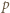 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 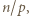 otrzymując
otrzymując 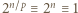 (mod
(mod 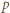 ). Zatem
). Zatem 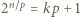 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 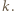 Stąd
Stąd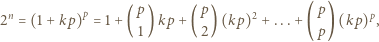
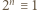 (mod
(mod 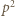 ); a to była nasza teza.
); a to była nasza teza.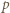 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 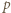 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 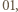 czyli wykładnik
czyli wykładnik 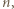 dla którego
dla którego 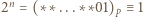 (mod
(mod 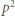 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 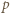 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 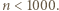 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 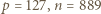 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 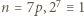 (mod
(mod 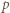 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 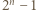 nie są względnie pierwsze.
nie są względnie pierwsze.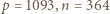 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 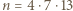 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 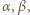 dla których
dla których 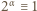 (mod 7),
(mod 7), 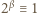 (mod 13), to
(mod 13), to 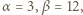 więc wykładnik
więc wykładnik 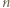 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 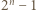 przez
przez 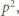 zatem liczba
zatem liczba 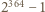 nie jest bezkwadratowa.
nie jest bezkwadratowa.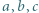 spełniają nierówność
spełniają nierówność 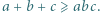 Udowodnić, że
Udowodnić, że 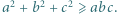
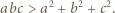
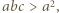 skąd
skąd 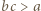 i analogicznie
i analogicznie 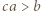 oraz
oraz 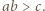 Ponadto mamy
Ponadto mamy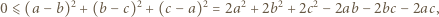
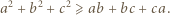
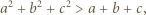
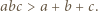
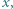 dla których każda z liczb
dla których każda z liczb 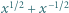 oraz
oraz 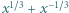 jest całkowita.
jest całkowita.
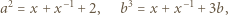
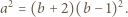
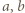 są naturalne, czynnik
są naturalne, czynnik 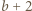 musi być kwadratem liczby naturalnej; więc
musi być kwadratem liczby naturalnej; więc 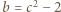
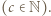 Zgodnie z (1), jest to suma liczb
Zgodnie z (1), jest to suma liczb 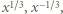 których iloczyn wynosi 1. Zatem
których iloczyn wynosi 1. Zatem 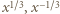 to pierwiastki trójmianu kwadratowego
to pierwiastki trójmianu kwadratowego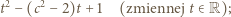
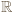 ) gdy
) gdy 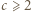 ; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek:
; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek: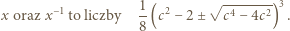
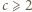 określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:
określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:  oraz
oraz 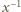 (jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas
(jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas 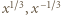 są pierwiastkami trójmianu (3); ich suma wynosi
są pierwiastkami trójmianu (3); ich suma wynosi 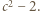 Liczby
Liczby 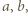 zdefiniowane wzorami (1), spełniają równość (2); a ponieważ
zdefiniowane wzorami (1), spełniają równość (2); a ponieważ 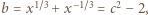 zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba
zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba 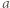 jest całkowita (liczba
jest całkowita (liczba 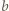 oczywiście też).
oczywiście też).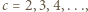 przedstawia ogólną postać liczb
przedstawia ogólną postać liczb 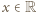 o rozważanej w zadaniu własności.
o rozważanej w zadaniu własności.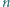 -kąta foremnego wpisanego w okrąg o promieniu 1.
-kąta foremnego wpisanego w okrąg o promieniu 1.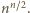
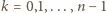 oraz
oraz 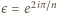 niech
niech 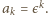 Wówczas liczby
Wówczas liczby 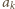 wyznaczają na płaszczyźnie zespolonej
wyznaczają na płaszczyźnie zespolonej  -kąt foremny wpisany w okrąg o promieniu
-kąt foremny wpisany w okrąg o promieniu 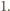
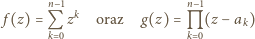
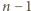 mają równe współczynniki przy najwyższej potędze
mają równe współczynniki przy najwyższej potędze  oraz
oraz 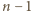 wspólnych pierwiastków zespolonych, mianowicie
wspólnych pierwiastków zespolonych, mianowicie 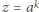 dla
dla 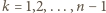 (ze względu na równość
(ze względu na równość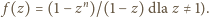
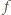 i
i 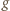 są równe, w szczególności
są równe, w szczególności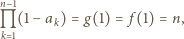
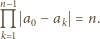
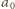 rozważanego wielokąta (czyli, z uwagi na symetrię, dowolny ustalony wierzchołek) jest równa
rozważanego wielokąta (czyli, z uwagi na symetrię, dowolny ustalony wierzchołek) jest równa 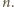 Wobec tego
Wobec tego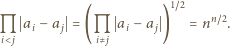
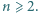 Wykazać, że dla każdego układu dodatnich liczb całkowitych
Wykazać, że dla każdego układu dodatnich liczb całkowitych 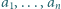 zachodzi nierówność
zachodzi nierówność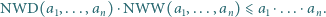
 ) te układy
) te układy 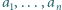 (dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.
(dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.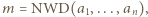
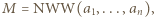
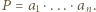 Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn
Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn 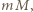 wchodzi do iloczynu
wchodzi do iloczynu 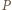 w co najmniej takiej samej potędze. Niech więc
w co najmniej takiej samej potędze. Niech więc 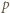 będzie liczbą pierwszą i niech (dla
będzie liczbą pierwszą i niech (dla 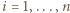 )
) 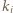 będzie takim wykładnikiem, że
będzie takim wykładnikiem, że 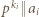 (ten napis oznacza, że
(ten napis oznacza, że 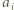 dzieli się przez
dzieli się przez 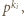 ale nie przez
ale nie przez 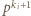 ). Wówczas
). Wówczas 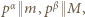 gdzie
gdzie 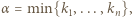
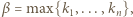 i wobec tego
i wobec tego 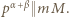 Oczywiście
Oczywiście 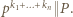 Porównanie wykładników nie pozostawia wątpliwości:
Porównanie wykładników nie pozostawia wątpliwości:
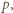 uzasadnia to zadaną nierówność
uzasadnia to zadaną nierówność 
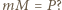 Wtedy, gdy każda liczba pierwsza dzieli
Wtedy, gdy każda liczba pierwsza dzieli 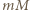 w dokładnie tej samej potędze, w jakiej dzieli
w dokładnie tej samej potędze, w jakiej dzieli 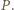 Czyli gdy dla każdej liczby pierwszej
Czyli gdy dla każdej liczby pierwszej 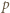 nierówność (1) (z wykładnikami
nierówność (1) (z wykładnikami 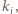 wyznaczonymi przez
wyznaczonymi przez 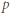 ) staje się równością.
) staje się równością.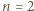 jest tak zawsze; dostajemy znaną tożsamość:
jest tak zawsze; dostajemy znaną tożsamość: 
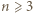 równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb
równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb 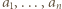 może dzielić się przez
może dzielić się przez 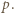 Wobec dowolności
Wobec dowolności 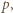 znaczy to, że liczby
znaczy to, że liczby 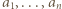 są parami względnie pierwsze.
są parami względnie pierwsze.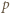 mamy w ciągu
mamy w ciągu 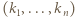 co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji
co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji 
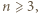 równość
równość 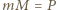 zachodzi wtedy i tylko wtedy, gdy liczby
zachodzi wtedy i tylko wtedy, gdy liczby 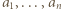 są parami względnie pierwsze; dla
są parami względnie pierwsze; dla 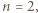 ta równość jest tożsamością.
ta równość jest tożsamością.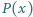 będzie takim wielomianem o współczynnikach rzeczywistych, że
będzie takim wielomianem o współczynnikach rzeczywistych, że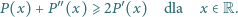
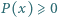 dla
dla 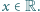
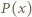 jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że
jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że 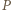 jest wielomianem stopnia dodatniego. Wielomian
jest wielomianem stopnia dodatniego. Wielomian 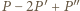 ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian
ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian 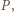 jak i wielomian
jak i wielomian 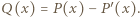 Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę
Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę  przy
przy  przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc
przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc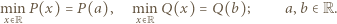
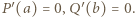 Zauważmy, że, w myśl założenia zadania,
Zauważmy, że, w myśl założenia zadania,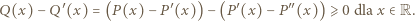
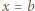 dostajemy
dostajemy 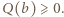 Jest to wartość minimalna wielomianu
Jest to wartość minimalna wielomianu 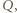 zatem
zatem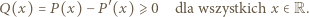
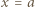 i mamy
i mamy 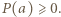 To wartość minimalna wielomianu
To wartość minimalna wielomianu 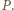 Zatem
Zatem 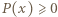 dla
dla 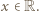
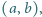 dla których liczba
dla których liczba
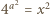 oraz
oraz 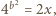 gdzie
gdzie 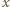 jest dodatnią liczbą całkowitą; wówczas liczba
jest dodatnią liczbą całkowitą; wówczas liczba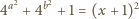
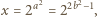
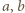 są powiązane zależnością
są powiązane zależnością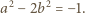
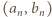 danych przez
danych przez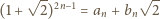
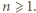
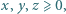 spełniające układ równań
spełniające układ równań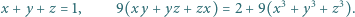
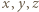 będą liczbami nieujemnymi, spełniającymi podany układ równań. Ich suma, więc i jej kwadrat, wynosi 1; wobec tego
będą liczbami nieujemnymi, spełniającymi podany układ równań. Ich suma, więc i jej kwadrat, wynosi 1; wobec tego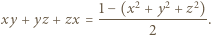
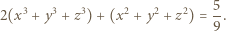
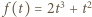 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale 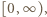 zatem spełnia nierówność Jensena
zatem spełnia nierówność Jensena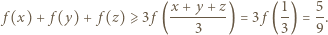
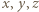 ) nierówność (2) staje się równością, co ma miejsce jedynie, gdy te liczby są równe. Ich suma jest jedynką, więc
) nierówność (2) staje się równością, co ma miejsce jedynie, gdy te liczby są równe. Ich suma jest jedynką, więc 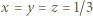 ; ta trójka liczb spełnia oba równania układu i stanowi jego jedyne rozwiązanie.
; ta trójka liczb spełnia oba równania układu i stanowi jego jedyne rozwiązanie.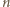 jest liczbą parzystą, to żądanym przedstawieniem jest
jest liczbą parzystą, to żądanym przedstawieniem jest 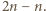
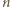 jest liczbą nieparzystą i niech
jest liczbą nieparzystą i niech 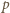 będzie najmniejszą nieparzystą liczbą pierwszą, która nie jest dzielnikiem liczby
będzie najmniejszą nieparzystą liczbą pierwszą, która nie jest dzielnikiem liczby 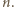 Wówczas przedstawienie liczby
Wówczas przedstawienie liczby  w postaci różnicy
w postaci różnicy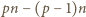
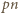 oraz
oraz 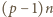 ma dokładnie te dzielniki pierwsze co liczba
ma dokładnie te dzielniki pierwsze co liczba 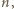 a ponadto po jednym dodatkowym - odpowiednio
a ponadto po jednym dodatkowym - odpowiednio 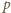 oraz
oraz 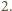
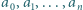 są takie, że
są takie, że 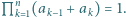 Udowodnić, że
Udowodnić, że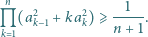
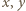 oraz dodatniej liczby całkowitej
oraz dodatniej liczby całkowitej 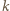 zachodzi nierówność
zachodzi nierówność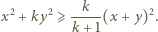
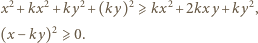
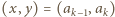 dla
dla 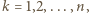 mnożąc otrzymane związki stronami i korzystając z założenia zadania, uzyskujemy
mnożąc otrzymane związki stronami i korzystając z założenia zadania, uzyskujemy 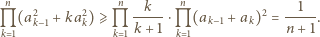
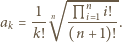
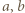 będą liczbami naturalnymi, spełniającymi warunek
będą liczbami naturalnymi, spełniającymi warunek 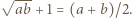 Wymierny pierwiastek z liczby naturalnej jest liczbą naturalną. Zatem
Wymierny pierwiastek z liczby naturalnej jest liczbą naturalną. Zatem 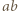 musi być kwadratem liczby naturalnej. Oznaczając przez
musi być kwadratem liczby naturalnej. Oznaczając przez 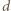 największy wspólny dzielnik liczb
największy wspólny dzielnik liczb 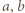 (tak, że
(tak, że 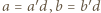 ;
; 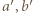 względnie pierwsze) widzimy, że czynniki
względnie pierwsze) widzimy, że czynniki 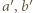 muszą być kwadratami:
muszą być kwadratami: 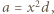
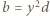 (
( 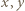 naturalne). Badane równanie przybiera postać
naturalne). Badane równanie przybiera postać 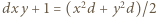 ; po przekształceniu:
; po przekształceniu: 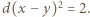 Stąd wniosek, że
Stąd wniosek, że 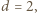
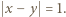
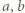 to podwojone kwadraty dwóch kolejnych liczb naturalnych. Proste sprawdzenie pokazuje, że każda taka para spełnia wymagany warunek.
to podwojone kwadraty dwóch kolejnych liczb naturalnych. Proste sprawdzenie pokazuje, że każda taka para spełnia wymagany warunek.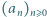 definiujemy rekurencyjnie:
definiujemy rekurencyjnie: 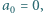
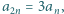
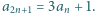 Scharakteryzuj wszystkie liczby całkowite
Scharakteryzuj wszystkie liczby całkowite 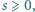 dla których istnieje dokładnie jedna para
dla których istnieje dokładnie jedna para 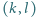 spełniająca warunki
spełniająca warunki 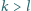 oraz
oraz 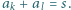
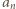 należy zapisać liczbę
należy zapisać liczbę 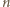 w systemie dwójkowym i odczytać w trójkowym.
w systemie dwójkowym i odczytać w trójkowym.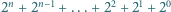 oraz
oraz 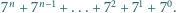
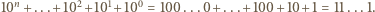 Podobnie szukane sumy równe są
Podobnie szukane sumy równe są 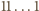 w odpowiednich systemach pozycyjnych. W dwójkowym liczba
w odpowiednich systemach pozycyjnych. W dwójkowym liczba 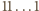 jest jak
jest jak 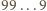 w dziesiętnym, więc pierwsza z sum to
w dziesiętnym, więc pierwsza z sum to 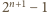 . Analogicznie dla drugiej sumy: w systemie siódemkowym
. Analogicznie dla drugiej sumy: w systemie siódemkowym 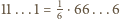 równe jest
równe jest 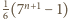 w dziesiętnym.
w dziesiętnym.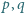
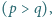 dla których także liczby
dla których także liczby 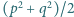 oraz
oraz 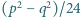 są pierwsze.
są pierwsze.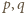 spełniają postawione warunki; w szczególności
spełniają postawione warunki; w szczególności 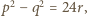 gdzie
gdzie  jest liczbą pierwszą. Jasne, że
jest liczbą pierwszą. Jasne, że 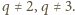 Iloczyn liczb naturalnych
Iloczyn liczb naturalnych 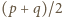 i
i 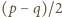 wynosi
wynosi 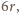 więc jedna z nich dzieli się przez
więc jedna z nich dzieli się przez 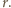 W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie
W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie 
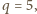 to
to 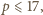 czyli
czyli 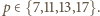 Sprawdzamy, że tylko para
Sprawdzamy, że tylko para 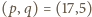 jest dobra.
jest dobra.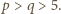 Wówczas
Wówczas 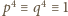 (mod 5), więc
(mod 5), więc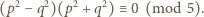
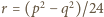 oraz
oraz 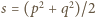 dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale
dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale 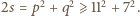 Pozostaje możliwość
Pozostaje możliwość 
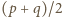 i
i 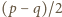 wynosi
wynosi 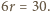 Cztery możliwe rozkłady
Cztery możliwe rozkłady 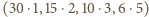 dają pary
dają pary 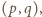 odpowiednio,
odpowiednio, 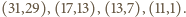 Ostatnia odpada. Dla
Ostatnia odpada. Dla 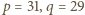 wychodzi
wychodzi 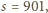 liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości
liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości  i
i  :
: