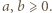Z tożsamości
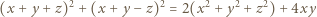
wynika, że zadane równanie jest równoważne następującemu:
 |
(1) |
Jest też równoważne każdemu z dwóch równań uzyskanych przez cykliczne przestawienie zmiennych w (1). Jeśli więc liczby całkowite 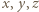 spełniają warunki zadania, to iloczyny
spełniają warunki zadania, to iloczyny 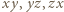 są nieujemne, co oznacza, że liczby
są nieujemne, co oznacza, że liczby 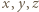 są wszystkie nieujemne lub wszystkie niedodatnie.
są wszystkie nieujemne lub wszystkie niedodatnie.
Weźmy przypadek, gdy 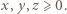 Ze związku (1) (oraz warunku, że
Ze związku (1) (oraz warunku, że 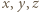 nie mają wspólnego dzielnika
nie mają wspólnego dzielnika 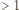 ) wynika, że
) wynika, że 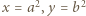 dla pewnej pary liczb całkowitych
dla pewnej pary liczb całkowitych 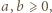 względnie pierwszych. Przepisujemy (1) jako
względnie pierwszych. Przepisujemy (1) jako 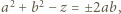 czyli
czyli 
Uwzględniając pominięty przypadek, gdy 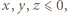 widzimy, że trójka
widzimy, że trójka 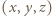 ma postać
ma postać
 |
(2) |
Na odwrót, jeśli trójka liczb całkowitych 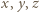 ma taką postać (więc
ma taką postać (więc 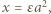
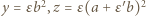 ;
; 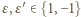 ), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby
), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby 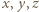 są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
Można sformułować tę odpowiedź w formie bardziej symetryczej, pisząc, że liczby 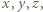 po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
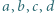 zachodzi nierówność
zachodzi nierówność

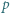 będzie nieparzystą liczbą pierwszą oraz
będzie nieparzystą liczbą pierwszą oraz 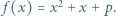 Przypuśćmy, że liczba
Przypuśćmy, że liczba 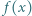 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej  nie większej od
nie większej od 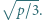 Wykazać, że liczba
Wykazać, że liczba 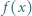 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej 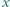 nie większej od
nie większej od 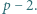
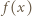 jest liczbą złożoną dla pewnego
jest liczbą złożoną dla pewnego 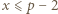 i oznaczmy przez
i oznaczmy przez  najmniejszą taką dodatnią liczbę całkowitą, że
najmniejszą taką dodatnią liczbę całkowitą, że 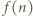 jest liczbą złożoną. Z założeń zadania wynika, że
jest liczbą złożoną. Z założeń zadania wynika, że 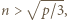 czyli
czyli 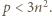
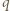 najmniejszy dzielnik pierwszy liczby
najmniejszy dzielnik pierwszy liczby 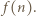 Zauważmy, że
Zauważmy, że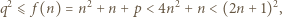
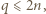 czyli istnieje liczba całkowita
czyli istnieje liczba całkowita 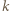 o tej własności, że
o tej własności, że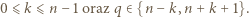
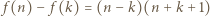
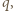 więc skoro
więc skoro 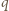 dzieli
dzieli 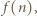 to również
to również 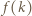 jest liczbą podzielną przez
jest liczbą podzielną przez 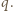 Pozostaje zauważyć, że
Pozostaje zauważyć, że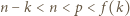
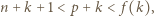
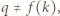 a co za tym idzie -
a co za tym idzie - 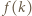 jest liczbą złożoną. Jednak
jest liczbą złożoną. Jednak 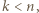 więc stoi to w sprzeczności z wyborem liczby
więc stoi to w sprzeczności z wyborem liczby 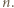
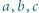 spełniają równości
spełniają równości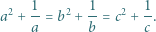
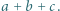
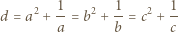
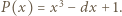 Skoro
Skoro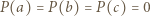
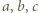 są różne, to są one różnymi pierwiastkami wielomianu
są różne, to są one różnymi pierwiastkami wielomianu 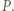 Stąd na mocy wzorów Viéte'a uzyskujemy
Stąd na mocy wzorów Viéte'a uzyskujemy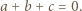
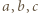 spełniające założenia zadania rzeczywiście istnieją, np.
spełniające założenia zadania rzeczywiście istnieją, np.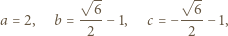
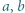 spełniają równość
spełniają równość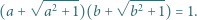
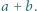
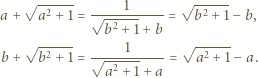
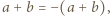 czyli
czyli 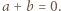
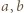 spełniające założenia zadania rzeczywiście istnieją (np.
spełniające założenia zadania rzeczywiście istnieją (np. 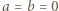 ), więc znaleziona wartość 0 istotnie jest osiągalna.
), więc znaleziona wartość 0 istotnie jest osiągalna.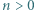 i
i 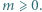 Ile rozwiązań w liczbach całkowitych nieujemnych ma równanie
Ile rozwiązań w liczbach całkowitych nieujemnych ma równanie 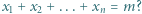
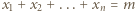 należy sparować z ciągiem binarnym
należy sparować z ciągiem binarnym 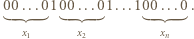
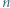 równania
równania 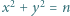 i
i 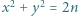 spełnia tyle samo par liczb całkowitych
spełnia tyle samo par liczb całkowitych 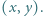
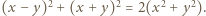
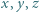 spełniające równanie
spełniające równanie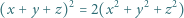
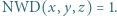
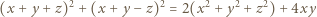

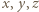 spełniają warunki zadania, to iloczyny
spełniają warunki zadania, to iloczyny 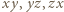 są nieujemne, co oznacza, że liczby
są nieujemne, co oznacza, że liczby 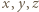 są wszystkie nieujemne lub wszystkie niedodatnie.
są wszystkie nieujemne lub wszystkie niedodatnie.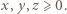 Ze związku (1) (oraz warunku, że
Ze związku (1) (oraz warunku, że 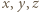 nie mają wspólnego dzielnika
nie mają wspólnego dzielnika 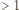 ) wynika, że
) wynika, że 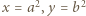 dla pewnej pary liczb całkowitych
dla pewnej pary liczb całkowitych 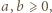 względnie pierwszych. Przepisujemy (1) jako
względnie pierwszych. Przepisujemy (1) jako 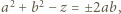 czyli
czyli 
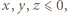 widzimy, że trójka
widzimy, że trójka 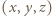 ma postać
ma postać
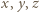 ma taką postać (więc
ma taką postać (więc 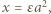
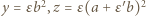 ;
; 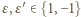 ), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby
), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby 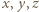 są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.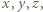 po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych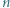 o tej własności, że
o tej własności, że 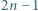 jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych
jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych 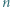 różnych dodatnich liczb całkowitych można wskazać takie dwie liczby
różnych dodatnich liczb całkowitych można wskazać takie dwie liczby 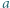 i
i 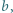 że
że
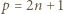 i rozważmy dowolne liczby całkowite
i rozważmy dowolne liczby całkowite 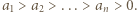 Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od
Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od 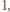 to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że
to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że 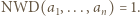
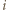 o tej własności, że
o tej własności, że 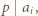 to dla pewnego
to dla pewnego 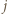 mamy
mamy 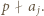 Wówczas
Wówczas 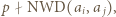 więc
więc
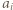 nie jest podzielna przez
nie jest podzielna przez 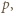 to reszty z dzielenia przez
to reszty z dzielenia przez 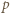 pewnych dwóch z nich należą do tego samego spośród
pewnych dwóch z nich należą do tego samego spośród 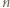 zbiorów
zbiorów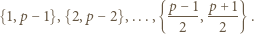
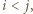 że
że 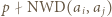 oraz
oraz 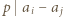 lub
lub 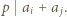 W pierwszym przypadku mamy
W pierwszym przypadku mamy
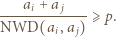
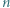 o tej własności, że
o tej własności, że 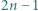 jest liczbą złożoną. Skonstruować zbiór
jest liczbą złożoną. Skonstruować zbiór 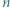 różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru
różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru 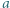 i
i 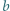 zachodzi nierówność
zachodzi nierówność
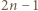 jest liczbą złożoną, to
jest liczbą złożoną, to 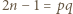 dla pewnych (niekoniecznie różnych) liczb nieparzystych
dla pewnych (niekoniecznie różnych) liczb nieparzystych 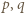 większych od
większych od 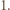 Niech
Niech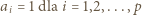
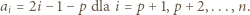
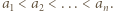
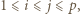 to
to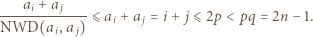
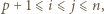 to
to 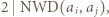 skąd
skąd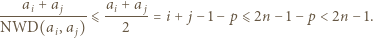
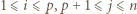 oraz
oraz 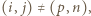 to
to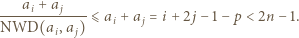
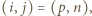 to
to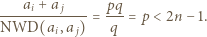

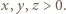 Odejmując stronami drugie równanie od pierwszego, otrzymamy
Odejmując stronami drugie równanie od pierwszego, otrzymamy 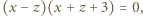 co daje
co daje 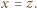

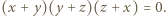

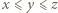 i odejmując stronami trzecie równanie od drugiego, otrzymamy
i odejmując stronami trzecie równanie od drugiego, otrzymamy 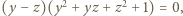 więc
więc 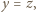 bo drugi nawias jest dodatni.
bo drugi nawias jest dodatni.
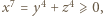 więc
więc 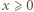 ; analogicznie
; analogicznie 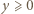 i
i 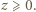 Załóżmy, że
Załóżmy, że 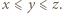 Wówczas prawe strony równań są uporządkowane niemalejąco, a lewe nierosnąco, więc muszą być wszystkie równe.
Wówczas prawe strony równań są uporządkowane niemalejąco, a lewe nierosnąco, więc muszą być wszystkie równe.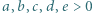 jest równa sumie sześcianów dwóch pozostałych. Wyznaczyć te liczby.
jest równa sumie sześcianów dwóch pozostałych. Wyznaczyć te liczby.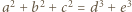 oraz
oraz 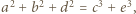 otrzymamy
otrzymamy 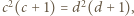 z czego można wywnioskować, że
z czego można wywnioskować, że 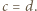
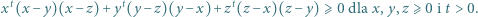
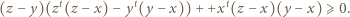
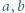 i
i  są naturalne. Iloczyn dowolnych dwóch spośród nich daje resztę
są naturalne. Iloczyn dowolnych dwóch spośród nich daje resztę 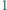 z dzielenia przez trzecią. Wyznaczyć te liczby.
z dzielenia przez trzecią. Wyznaczyć te liczby.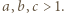 Można uzasadnić, że
Można uzasadnić, że 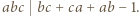 Ograniczamy się do przypadku, w którym
Ograniczamy się do przypadku, w którym 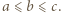 Mamy
Mamy  więc musi być
więc musi być 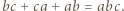 Dla
Dla 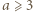 otrzymujemy sprzeczność, więc
otrzymujemy sprzeczność, więc 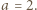
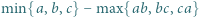 dla liczb rzeczywistych
dla liczb rzeczywistych 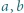 i
i 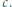
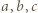 występują liczby ujemne, to
występują liczby ujemne, to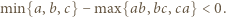
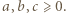 Można przyjąć
Można przyjąć 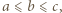 wystarczy użyć oszacowania
wystarczy użyć oszacowania 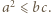
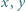 i
i  spełniają warunki:
spełniają warunki:
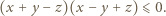

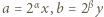 i
i 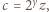 gdzie
gdzie 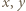 i
i  są liczbami nieparzystymi. Ograniczamy się do przypadku
są liczbami nieparzystymi. Ograniczamy się do przypadku 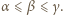 Należy podzielić obie strony równania przez
Należy podzielić obie strony równania przez 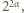 a następnie przeanalizować ich reszty z dzielenia przez
a następnie przeanalizować ich reszty z dzielenia przez 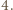
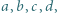 które jednocześnie spełniają nierówności
które jednocześnie spełniają nierówności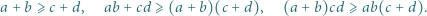
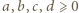 będą liczbami o rozważanej własności. Wielomian o pierwiastkach
będą liczbami o rozważanej własności. Wielomian o pierwiastkach 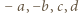
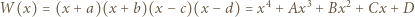
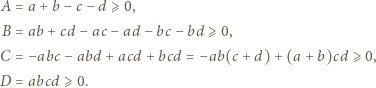
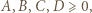 zatem
zatem 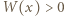 dla
dla 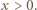 Brak pierwiastków dodatnich oznacza, że
Brak pierwiastków dodatnich oznacza, że 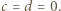
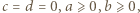 zadane nierówności są spełnione. Rozwiązaniem zadania są czwórki
zadane nierówności są spełnione. Rozwiązaniem zadania są czwórki 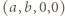 z
z