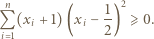Trzy rodzaje indukcji matematycznej»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Trzy rodzaje indukcji matematycznej
- Publikacja w Delcie: lipiec 2019
- Publikacja elektroniczna: 1 lipca 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (410 KB)
Udowodnić nierówność Bernoulliego: 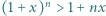 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 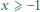 i liczb naturalnych
i liczb naturalnych 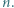
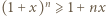 przez liczbę dodatnią
przez liczbę dodatnią 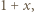 następnie wystarczy udowodnić, że
następnie wystarczy udowodnić, że 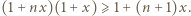
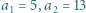 oraz
oraz 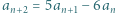 dla
dla 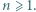 Wykazać, że
Wykazać, że 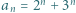 dla wszystkich naturalnych
dla wszystkich naturalnych 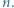
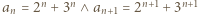 należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej
należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej 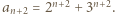
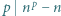 dla każdej liczby pierwszej
dla każdej liczby pierwszej 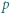 i liczby naturalnej
i liczby naturalnej 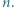
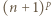 oraz fakt, że
oraz fakt, że 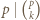 dla
dla 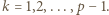
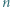 będzie liczbą naturalną. Dowieść, że istnieje
będzie liczbą naturalną. Dowieść, że istnieje  -cyfrowa wielokrotność liczby
-cyfrowa wielokrotność liczby 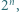 w której zapisie dziesiętnym występują tylko cyfry
w której zapisie dziesiętnym występują tylko cyfry 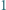 i
i 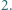
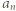 będzie poszukiwaną
będzie poszukiwaną 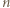 -cyfrową wielokrotnością liczby
-cyfrową wielokrotnością liczby 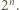 Szukaną wielokrotnością
Szukaną wielokrotnością 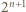 jest jedna z liczb:
jest jedna z liczb: 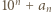 lub
lub 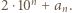
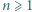 stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos
stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos 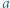 monet ze stosem
monet ze stosem 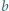 monet, to zapisujemy iloczyn
monet, to zapisujemy iloczyn 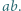 Te czynności wykonujemy aż do uzyskania jednego stosu
Te czynności wykonujemy aż do uzyskania jednego stosu 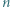 monet. Dowieść, że suma zapisanych iloczynów wynosi
monet. Dowieść, że suma zapisanych iloczynów wynosi 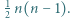
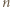 -kątów, w których
-kątów, w których 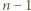 i
i 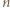 są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości
są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości 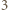 polega na dodaniu trzech wierzchołków z liczbami
polega na dodaniu trzech wierzchołków z liczbami 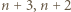 i
i 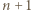 pomiędzy tymi dwoma.
pomiędzy tymi dwoma.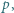 które można zapisać w postaci sumy
które można zapisać w postaci sumy 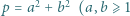 całkowite) tak, by liczba
całkowite) tak, by liczba 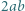 była kwadratem liczby całkowitej.
była kwadratem liczby całkowitej.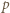 będzie liczbą pierwszą o rozważanej własności:
będzie liczbą pierwszą o rozważanej własności: 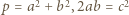 (
( 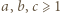 całkowite). Oznaczmy
całkowite). Oznaczmy 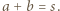 Tak więc
Tak więc 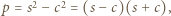 wobec czego
wobec czego 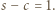 Równość
Równość 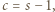 po podniesieniu stronami do kwadratu i podstawieniu wyrażeń określających
po podniesieniu stronami do kwadratu i podstawieniu wyrażeń określających 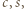 przybiera postać
przybiera postać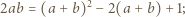
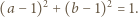
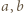 jest równa 2, a druga 1, i ostatecznie
jest równa 2, a druga 1, i ostatecznie 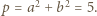 Skoro
Skoro 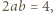 zatem liczba pierwsza
zatem liczba pierwsza 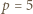 spełnia wymagane warunki, i jest to jedyna taka liczba.
spełnia wymagane warunki, i jest to jedyna taka liczba.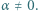 Funkcja
Funkcja 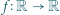 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 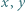 równanie
równanie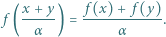
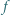 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 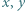 równanie
równanie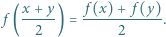
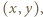 a drugi raz dla
a drugi raz dla 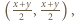 uzyskujemy
uzyskujemy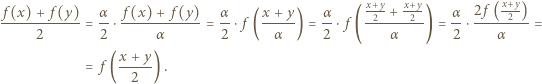
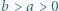 oraz parzystej liczby naturalnej
oraz parzystej liczby naturalnej 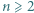 wyznaczyć kres górny wartości stosunku
wyznaczyć kres górny wartości stosunku 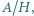 gdzie
gdzie 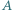 i
i 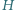 to (odpowiednio) średnia arytmetyczna i średnia harmoniczna
to (odpowiednio) średnia arytmetyczna i średnia harmoniczna 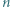 liczb wybranych dowolnie z przedziału
liczb wybranych dowolnie z przedziału ![[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/7x-ef372a8dfa93edadbc34939244d39cca0f9e4c26-im-2C,6B,73-FF,FF,FF.gif)
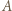 i
i 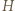 liczb
liczb ![x1, | ...,xn ∈[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/3x-bed5f731d399079efabe3448810444f970457e80-im-66,57,43-FF,FF,FF.gif) Weźmy dowolną liczbę
Weźmy dowolną liczbę 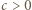 i zauważmy, że
i zauważmy, że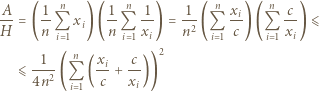
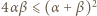 dla liczb
dla liczb 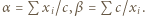
![x ∈ [a,b]](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/1x-2643bd4bae04ef39ab2c2805c88b5fc400e1fac5-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 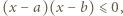 którą przepisujemy w postaci
którą przepisujemy w postaci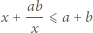
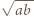 :
: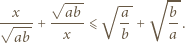
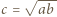 i korzystając z (2):
i korzystając z (2):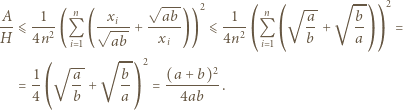
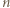 jest z założenia parzysta. Gdy
jest z założenia parzysta. Gdy 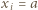 dla połowy spośród wskaźników
dla połowy spośród wskaźników 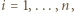 zaś
zaś 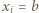 dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba
dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba 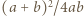 jest maksymalną wartością stosunku
jest maksymalną wartością stosunku 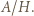
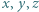 prawdziwa jest nierówność
prawdziwa jest nierówność
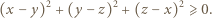

 i
i 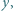 niebędących jednocześnie zerami.
niebędących jednocześnie zerami.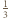 oraz
oraz 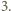 Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo
Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo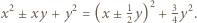
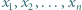 zachodzi nierówność
zachodzi nierówność
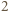 i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy
i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy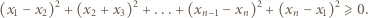

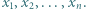
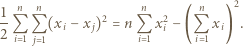
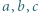 jest równa
jest równa 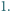 Udowodnić, że
Udowodnić, że
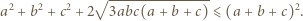
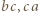 i
i 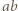 ułatwia dalsze rachunki.
ułatwia dalsze rachunki.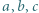 spełniają równość
spełniają równość 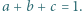 Wykazać, że
Wykazać, że
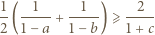
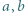 i
i  zachodzi nierówność
zachodzi nierówność
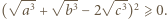
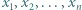 będą liczbami dodatnimi. Przyjmijmy
będą liczbami dodatnimi. Przyjmijmy 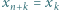 dla całkowitych
dla całkowitych 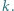 Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
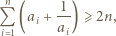
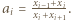
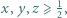 spełniających warunek
spełniających warunek 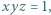 zachodzi nierówność
zachodzi nierówność
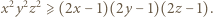
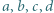 spełniają nierówność
spełniają nierówność
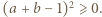
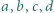 zachodzi nierówność
zachodzi nierówność
![x ,x ,...,x ∈ [−1,1] 1 2 n](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-19_05-kpm-12/1x-e242253ed078688e97a06aead3aec19a78e70a97-im-2C,6B,73-FF,FF,FF.gif) spełniają warunek
spełniają warunek 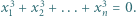 Dowieść, że
Dowieść, że