Niech 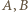 będzie parą zbiorów, spełniających wymienione warunki. Ponumerujmy te warunki, w podanej kolejności, (i), (ii), (iii), (iv).
będzie parą zbiorów, spełniających wymienione warunki. Ponumerujmy te warunki, w podanej kolejności, (i), (ii), (iii), (iv).
Gdyby liczba 0 była w zbiorze 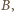 to dla każdej liczby
to dla każdej liczby 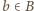 mielibyśmy (z war. (iv))
mielibyśmy (z war. (iv)) 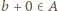 ; to by znaczyło, że zbiór
; to by znaczyło, że zbiór 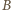 zawiera się w zbiorze
zawiera się w zbiorze 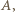 czyli (z war. (i))
czyli (z war. (i)) 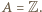 Wtedy (z war. (iii)) także
Wtedy (z war. (iii)) także 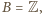 co daje sprzeczność z warunkiem (ii). Wniosek:
co daje sprzeczność z warunkiem (ii). Wniosek: 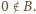 Warunek (i) wymusza konkluzję:
Warunek (i) wymusza konkluzję: 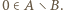 Stąd (i z war. (iii))
Stąd (i z war. (iii)) 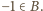
Gdyby liczba 1 była w zbiorze 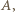 to (z war. (iii))
to (z war. (iii)) 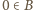 ; a przecież
; a przecież 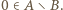 Tak więc
Tak więc 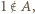 czyli (z war. (i))
czyli (z war. (i)) 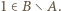
Wykażemy indukcyjnie, że dla każdej liczby całkowitej 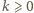 :
:
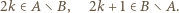 |
(*) |
Dla 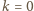 tak jest. Ustalmy liczbę
tak jest. Ustalmy liczbę 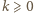 i przyjmijmy słuszność związków (*) dla tej liczby
i przyjmijmy słuszność związków (*) dla tej liczby 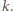 Przypuśćmy, że
Przypuśćmy, że 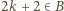 ; wtedy (z war. (iv))
; wtedy (z war. (iv)) 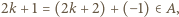 wbrew założeniu indukcyjnemu. Zatem
wbrew założeniu indukcyjnemu. Zatem 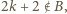 czyli (z war. (i))
czyli (z war. (i)) 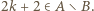
Przypuśćmy z kolei, że 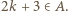 Wtedy (z war. (iii))
Wtedy (z war. (iii)) 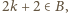 wbrew temu, co wykazaliśmy tuż przed chwilą. Zatem
wbrew temu, co wykazaliśmy tuż przed chwilą. Zatem 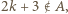 czyli (z war. (i))
czyli (z war. (i)) 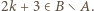 Uzyskaliśmy związki (*) z liczbą
Uzyskaliśmy związki (*) z liczbą 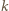 zastąpioną przez
zastąpioną przez 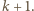 Z zasady indukcji własność (*) przysługuje wszystkim liczbom całkowitym nieujemnym.
Z zasady indukcji własność (*) przysługuje wszystkim liczbom całkowitym nieujemnym.
Teraz pokażemy, że ujemnym - też. Przypuśćmy, że 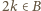 dla pewnej liczby
dla pewnej liczby 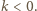 Wiemy już (własność (*)), że
Wiemy już (własność (*)), że 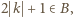 a więc (z war. (iv)):
a więc (z war. (iv)): 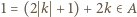 ; sprzeczność z wcześniejszym ustaleniem
; sprzeczność z wcześniejszym ustaleniem 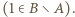 W takim razie
W takim razie 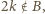 czyli (z war. (i))
czyli (z war. (i)) 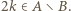
Wreszcie przypuśćmy, że 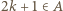 dla pewnej liczby
dla pewnej liczby 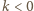 ; wtedy (z war. (iii))
; wtedy (z war. (iii)) 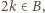 wbrew temu, co stwierdziliśmy przed chwilą. Zatem
wbrew temu, co stwierdziliśmy przed chwilą. Zatem 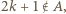 czyli (z war. (i))
czyli (z war. (i)) 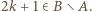
Mamy więc słuszność związków (*) dla wszystkich 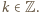 Mówią one, że
Mówią one, że 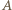 jest zbiorem wszystkich liczb parzystych, a
jest zbiorem wszystkich liczb parzystych, a 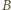 jest zbiorem wszystkich liczb nieparzystych. Ta para zbiorów spełnia, rzecz jasna, wymagane warunki - i jest to jedyna taka para.
jest zbiorem wszystkich liczb nieparzystych. Ta para zbiorów spełnia, rzecz jasna, wymagane warunki - i jest to jedyna taka para.
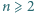 znaleźć najmniejszą wartość sumy
znaleźć najmniejszą wartość sumy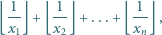
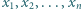 są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek
są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek 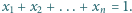
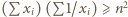 ; we wszystkich symbolach sumowania przyjmujemy
; we wszystkich symbolach sumowania przyjmujemy 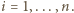 Przy warunku
Przy warunku 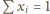 mamy więc
mamy więc 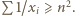 Dla każdej liczby rzeczywistej
Dla każdej liczby rzeczywistej 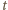 słuszne jest oszacowanie
słuszne jest oszacowanie 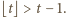 Stąd
Stąd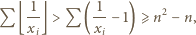
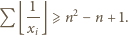
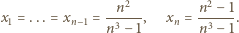
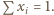 Dla
Dla 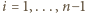 mamy przy tym
mamy przy tym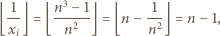
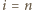 :
: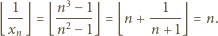
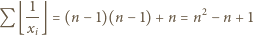
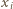 ; można dać wiele innych przykładów). Wniosek: liczba
; można dać wiele innych przykładów). Wniosek: liczba 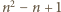 to szukane minimum.
to szukane minimum.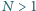 bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby
bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby 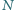 losujemy kolejno, bez zwracania, dwa dzielniki:
losujemy kolejno, bez zwracania, dwa dzielniki: 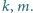 Rozważamy zdarzenia:
Rozważamy zdarzenia: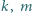 są względnie pierwsze;
są względnie pierwsze; jest podzielna przez
jest podzielna przez 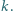
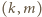 dzielników liczby
dzielników liczby 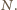 Zdarzenia
Zdarzenia 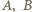 identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para
identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para 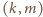 należy do
należy do 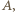 liczby
liczby 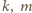 są względnie pierwszymi dzielnikami liczby
są względnie pierwszymi dzielnikami liczby 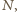 zatem także iloczyn
zatem także iloczyn 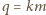 jest dzielnikiem
jest dzielnikiem 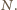 Oczywiście
Oczywiście 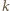 dzieli
dzieli 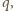 więc para
więc para 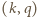 należy do
należy do 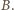
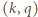 jest dowolną parą ze zbioru
jest dowolną parą ze zbioru 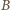 (więc
(więc 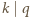 ), wtedy iloraz
), wtedy iloraz 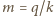 też jest dzielnikiem
też jest dzielnikiem 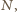 i to względnie pierwszym z
i to względnie pierwszym z 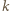 (bo gdyby
(bo gdyby 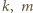 miały wspólny dzielnik
miały wspólny dzielnik 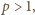 liczba
liczba 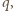 więc i
więc i 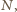 byłaby podzielna przez
byłaby podzielna przez 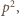 wbrew założeniu zadania). Zatem para
wbrew założeniu zadania). Zatem para 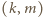 należy do
należy do 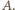
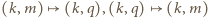 są wzajemnie odwrotne. Stąd wynika, że zbiory
są wzajemnie odwrotne. Stąd wynika, że zbiory 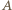 i
i 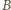 są równoliczne; zaś zdarzenia
są równoliczne; zaś zdarzenia 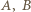 są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.
są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.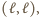 gdzie
gdzie 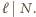 W poprzednim modelu, do zbioru
W poprzednim modelu, do zbioru 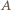 należała tylko jedna taka para
należała tylko jedna taka para 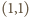 ; do
; do 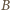 należały wszystkie. Więcej par zostało wyeliminowanych z
należały wszystkie. Więcej par zostało wyeliminowanych z 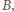 wobec czego (przy losowaniu bez zwracania) zdarzenie
wobec czego (przy losowaniu bez zwracania) zdarzenie 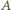 jest bardziej prawdopodobne niż
jest bardziej prawdopodobne niż 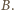
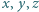 prawdziwa jest nierówność
prawdziwa jest nierówność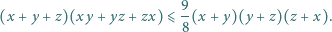
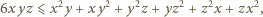
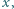 które spełniają równanie
które spełniają równanie 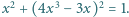
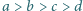 spełniają równanie
spełniają równanie
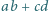 nie jest liczbą pierwszą.
nie jest liczbą pierwszą.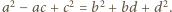 Rozważmy taki czworokąt
Rozważmy taki czworokąt 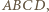 że
że 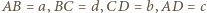 oraz
oraz 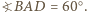 Z twierdzenia cosinusów zastosowanego do trójkątów
Z twierdzenia cosinusów zastosowanego do trójkątów 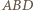 oraz
oraz 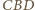 otrzymujemy wówczas
otrzymujemy wówczas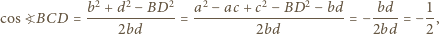
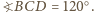
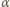 miarę kąta
miarę kąta 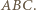 Wówczas
Wówczas 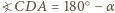 i korzystając z twierdzenia cosinusów tym razem w trójkątach
i korzystając z twierdzenia cosinusów tym razem w trójkątach 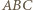 i
i 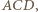 dostajemy
dostajemy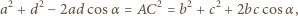
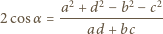
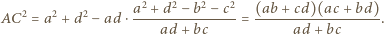
 jest wpisany w okrąg, to z twierdzenia Ptolemeusza wynika równość
jest wpisany w okrąg, to z twierdzenia Ptolemeusza wynika równość 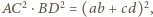 którą - korzystając z wcześniejszych obserwacji - możemy przepisać w postaci
którą - korzystając z wcześniejszych obserwacji - możemy przepisać w postaci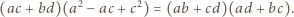
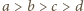 wynikają zależności
wynikają zależności 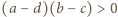 oraz
oraz 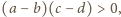 z których otrzymujemy ciąg nierówności
z których otrzymujemy ciąg nierówności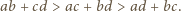
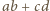 jest pierwsza, to biorąc pod uwagę powyższe nierówności, widzimy, że jest ona względnie pierwsza z liczbami
jest pierwsza, to biorąc pod uwagę powyższe nierówności, widzimy, że jest ona względnie pierwsza z liczbami 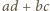 oraz
oraz 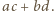 Z otrzymanej przez nas równości otrzymujemy więc podzielność
Z otrzymanej przez nas równości otrzymujemy więc podzielność 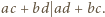 To jednak przeczy drugiej z powyższych nierówności i w efekcie dowodzi, że liczba
To jednak przeczy drugiej z powyższych nierówności i w efekcie dowodzi, że liczba 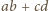 jest złożona.
jest złożona.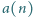 oznacza odległość liczby naturalnej
oznacza odległość liczby naturalnej 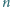 od najbliższej liczby, będącej pełnym kwadratem:
od najbliższej liczby, będącej pełnym kwadratem: 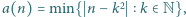 i niech
i niech 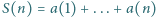 oraz
oraz 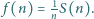 Udowodnić, że każda dodatnia liczba całkowita występuje w ciągu
Udowodnić, że każda dodatnia liczba całkowita występuje w ciągu 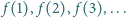 dokładnie trzykrotnie.
dokładnie trzykrotnie.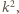 mają postać
mają postać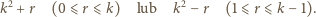
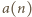 dla tych liczb wynosi
dla tych liczb wynosi 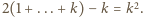 Stąd
Stąd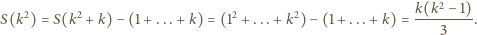
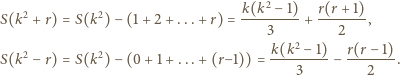
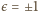 i wyznaczamy
i wyznaczamy 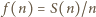 (dla
(dla 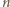 w formie (1)):
w formie (1)):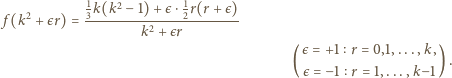

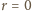 oraz
oraz 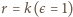 wychodzą wartości niecałkowite - można je zignorować, ograniczając zakres parametru
wychodzą wartości niecałkowite - można je zignorować, ograniczając zakres parametru  do
do 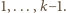 Wówczas
Wówczas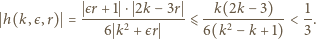
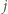 ) wtedy i tylko wtedy, gdy
) wtedy i tylko wtedy, gdy 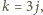 zaś
zaś 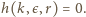 Gdy
Gdy 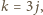 ostatni warunek
ostatni warunek 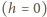 jest spełniony dla trzech par
jest spełniony dla trzech par 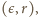 mianowicie
mianowicie 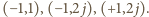
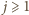 jest wartością wyrażenia
jest wartością wyrażenia 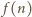 jedynie dla
jedynie dla 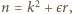 gdzie
gdzie 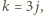 zaś
zaś  jest jedną z trzech powyższych par - czyli, po podstawieniu, dla
jest jedną z trzech powyższych par - czyli, po podstawieniu, dla 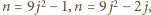
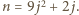
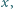 dla których każda z liczb
dla których każda z liczb 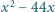 oraz
oraz 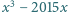 jest wymierna.
jest wymierna.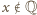 będzie taką liczbą, że
będzie taką liczbą, że 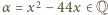 oraz
oraz 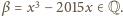 Tak więc
Tak więc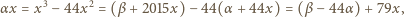
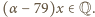 Skoro
Skoro 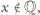 musi być
musi być 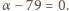 Dostajemy równanie
Dostajemy równanie 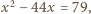 z rozwiązaniami
z rozwiązaniami 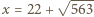 oraz
oraz 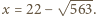 Obie wartości spełniają wymagane warunki
Obie wartości spełniają wymagane warunki 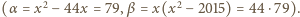
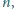
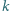 oraz takie nieujemne liczby rzeczywiste
oraz takie nieujemne liczby rzeczywiste 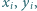 że
że 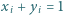 dla każdego
dla każdego 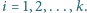 Wykaż, że zachodzi nierówność
Wykaż, że zachodzi nierówność
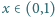 oraz dowolnych dodatnich liczb całkowitych
oraz dowolnych dodatnich liczb całkowitych 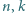 zachodzi nierówność
zachodzi nierówność

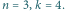
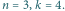
 wierszach i
wierszach i 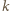 kolumnach, której każde pole pomalowano na czarno z prawdopodobieństwem
kolumnach, której każde pole pomalowano na czarno z prawdopodobieństwem 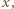 a z prawdopodobieństwem
a z prawdopodobieństwem 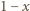 pozostawiono białe. Prawdopodobieństwo, że wybrany wiersz jest cały czarny jest wówczas równe
pozostawiono białe. Prawdopodobieństwo, że wybrany wiersz jest cały czarny jest wówczas równe 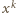 (bo każde z
(bo każde z 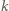 pól musi być czarne), więc prawdopodobieństwo, że istnieje w nim białe pole wynosi
pól musi być czarne), więc prawdopodobieństwo, że istnieje w nim białe pole wynosi 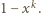
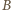 oznacza zdarzenie: w każdym wierszu jest co najmniej jedno białe pole. Wierszy jest
oznacza zdarzenie: w każdym wierszu jest co najmniej jedno białe pole. Wierszy jest  ; wobec powyższej obserwacji
; wobec powyższej obserwacji 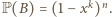 Analogicznie niech
Analogicznie niech 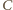 oznacza zdarzenie: w każdej kolumnie istnieje pole czarne, wówczas
oznacza zdarzenie: w każdej kolumnie istnieje pole czarne, wówczas 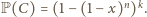
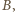 czyli nie jest prawdą, że w każdym wierszu jest białe pole, to istnieje wiersz o wszystkich polach czarnych. Wtedy na pewno w każdej kolumnie jest czarne pole (choćby z tego właśnie wiersza), czyli zachodzi zdarzenie
czyli nie jest prawdą, że w każdym wierszu jest białe pole, to istnieje wiersz o wszystkich polach czarnych. Wtedy na pewno w każdej kolumnie jest czarne pole (choćby z tego właśnie wiersza), czyli zachodzi zdarzenie 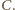 Wobec tego zawsze zachodzi co najmniej jedno spośród zdarzeń
Wobec tego zawsze zachodzi co najmniej jedno spośród zdarzeń 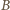 i
i 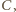 stąd
stąd 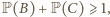 czyli
czyli 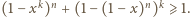
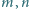 będą takimi dodatnimi liczbami całkowitymi, że w zbiorze
będą takimi dodatnimi liczbami całkowitymi, że w zbiorze 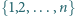 znajduje się dokładnie
znajduje się dokładnie 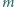 liczb pierwszych. Dowieść, że wśród dowolnych
liczb pierwszych. Dowieść, że wśród dowolnych 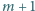 różnych liczb z tego zbioru można znaleźć liczbę, która jest dzielnikiem iloczynu pozostałych
różnych liczb z tego zbioru można znaleźć liczbę, która jest dzielnikiem iloczynu pozostałych  liczb.
liczb. oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej 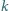 w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych
w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych 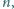 że
że 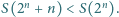
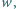 niebędąca liczbą całkowitą, że potęga
niebędąca liczbą całkowitą, że potęga 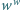 jest liczbą wymierną.
jest liczbą wymierną.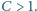 Ciąg dodatnich liczb rzeczywistych
Ciąg dodatnich liczb rzeczywistych 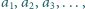 w którym
w którym 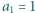 i
i 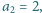 spełnia warunki
spełnia warunki 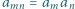 oraz
oraz 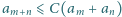 dla
dla 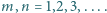 Dowieść, że
Dowieść, że 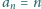 dla
dla 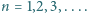
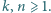 Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające
Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające 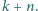 Ruch polega na zamianie miejscami dwóch liczb różniących się o
Ruch polega na zamianie miejscami dwóch liczb różniących się o 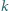 albo o
albo o 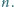 Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności
Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności 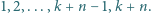
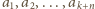 oznacza dany ciąg. Niech
oznacza dany ciąg. Niech 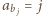 dla
dla 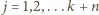 - ta równość definiuje jednoznacznie liczbę
- ta równość definiuje jednoznacznie liczbę 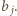 Dla ciągu
Dla ciągu 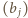 ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości
ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości 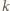 lub
lub 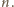 Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg
Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg 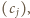 przyjmując, że
przyjmując, że 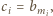 gdzie
gdzie 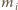 oznacza tę liczbę spośród
oznacza tę liczbę spośród 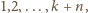 dla której różnica
dla której różnica 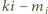 jest podzielna przez
jest podzielna przez 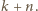 Ponieważ
Ponieważ 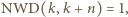 więc ciąg
więc ciąg 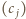 to permutacja ciągu
to permutacja ciągu 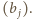 Ruchy w ciągu
Ruchy w ciągu 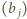 odpowiadają zamianie kolejnych wyrazów ciągu
odpowiadają zamianie kolejnych wyrazów ciągu 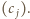 Do ciągu
Do ciągu 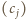 można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.
można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.
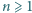 oraz
oraz 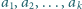 i
i 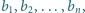 że
że 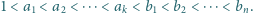 Wykazać, że jeżeli
Wykazać, że jeżeli 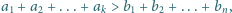 to
to 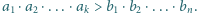
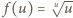 dla
dla 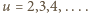 Udowodnimy, że
Udowodnimy, że 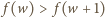 dla każdego
dla każdego 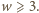 Bezpośrednie wymnożenie wskazuje, że
Bezpośrednie wymnożenie wskazuje, że 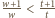 dla
dla 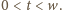 Zatem
Zatem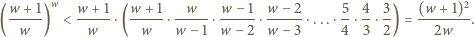
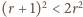 dla
dla 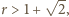 więc
więc 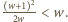 W efekcie
W efekcie 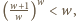 co jest równoważne nierówności
co jest równoważne nierówności 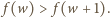 Ponieważ
Ponieważ 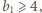 więc z zależności
więc z zależności 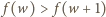 i związku
i związku 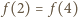 otrzymujemy
otrzymujemy 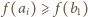 dla
dla 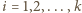 oraz
oraz 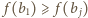 dla
dla 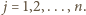 W myśl określenia funkcji
W myśl określenia funkcji 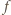 powyższe nierówności można zapisać w postaci
powyższe nierówności można zapisać w postaci 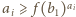 dla
dla 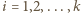 oraz
oraz 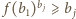 dla
dla 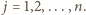 Stąd zaś, po wymnożeniu stronami i skorzystaniu z warunku (1), uzyskujemy
Stąd zaś, po wymnożeniu stronami i skorzystaniu z warunku (1), uzyskujemy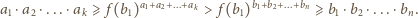
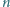 nazwiemy dobrą, jeżeli istnieje taka liczba pierwsza
nazwiemy dobrą, jeżeli istnieje taka liczba pierwsza 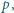 że liczba
że liczba  jest podzielna przez
jest podzielna przez 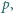 ale nie przez
ale nie przez 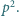 Wykazać, że wśród liczb
Wykazać, że wśród liczb 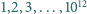 liczby dobre stanowią co najmniej
liczby dobre stanowią co najmniej 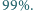
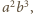 przy czym, oczywiście,
przy czym, oczywiście, 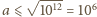 i
i 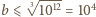 - jest tak ponieważ jeśli
- jest tak ponieważ jeśli 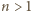 jest liczbą parzystą, to
jest liczbą parzystą, to 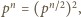 a jeśli
a jeśli 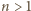 jest liczbą nieparzystą, to
jest liczbą nieparzystą, to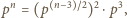
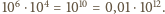
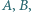 zawartych w zbiorze liczb całkowitych, o następujących własnościach:
zawartych w zbiorze liczb całkowitych, o następujących własnościach: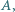
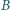 ;
;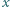 jest w zbiorze
jest w zbiorze 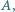 to liczba
to liczba 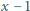 jest w zbiorze
jest w zbiorze 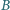 ;
;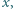
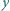 są w zbiorze
są w zbiorze 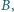 to liczba
to liczba 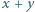 jest w zbiorze
jest w zbiorze 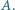
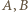 będzie parą zbiorów, spełniających wymienione warunki. Ponumerujmy te warunki, w podanej kolejności, (i), (ii), (iii), (iv).
będzie parą zbiorów, spełniających wymienione warunki. Ponumerujmy te warunki, w podanej kolejności, (i), (ii), (iii), (iv).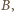 to dla każdej liczby
to dla każdej liczby 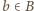 mielibyśmy (z war. (iv))
mielibyśmy (z war. (iv)) 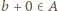 ; to by znaczyło, że zbiór
; to by znaczyło, że zbiór 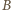 zawiera się w zbiorze
zawiera się w zbiorze 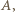 czyli (z war. (i))
czyli (z war. (i)) 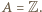 Wtedy (z war. (iii)) także
Wtedy (z war. (iii)) także 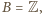 co daje sprzeczność z warunkiem (ii). Wniosek:
co daje sprzeczność z warunkiem (ii). Wniosek: 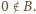 Warunek (i) wymusza konkluzję:
Warunek (i) wymusza konkluzję: 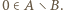 Stąd (i z war. (iii))
Stąd (i z war. (iii)) 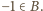
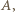 to (z war. (iii))
to (z war. (iii)) 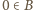 ; a przecież
; a przecież 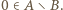 Tak więc
Tak więc 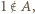 czyli (z war. (i))
czyli (z war. (i)) 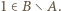
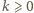 :
: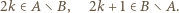
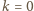 tak jest. Ustalmy liczbę
tak jest. Ustalmy liczbę 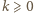 i przyjmijmy słuszność związków (*) dla tej liczby
i przyjmijmy słuszność związków (*) dla tej liczby 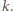 Przypuśćmy, że
Przypuśćmy, że 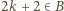 ; wtedy (z war. (iv))
; wtedy (z war. (iv)) 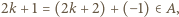 wbrew założeniu indukcyjnemu. Zatem
wbrew założeniu indukcyjnemu. Zatem 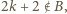 czyli (z war. (i))
czyli (z war. (i)) 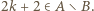
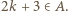 Wtedy (z war. (iii))
Wtedy (z war. (iii)) 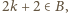 wbrew temu, co wykazaliśmy tuż przed chwilą. Zatem
wbrew temu, co wykazaliśmy tuż przed chwilą. Zatem 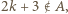 czyli (z war. (i))
czyli (z war. (i)) 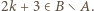 Uzyskaliśmy związki (*) z liczbą
Uzyskaliśmy związki (*) z liczbą 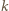 zastąpioną przez
zastąpioną przez 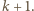 Z zasady indukcji własność (*) przysługuje wszystkim liczbom całkowitym nieujemnym.
Z zasady indukcji własność (*) przysługuje wszystkim liczbom całkowitym nieujemnym.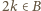 dla pewnej liczby
dla pewnej liczby 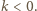 Wiemy już (własność (*)), że
Wiemy już (własność (*)), że 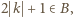 a więc (z war. (iv)):
a więc (z war. (iv)): 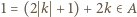 ; sprzeczność z wcześniejszym ustaleniem
; sprzeczność z wcześniejszym ustaleniem 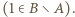 W takim razie
W takim razie 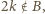 czyli (z war. (i))
czyli (z war. (i)) 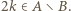
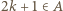 dla pewnej liczby
dla pewnej liczby 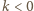 ; wtedy (z war. (iii))
; wtedy (z war. (iii)) 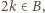 wbrew temu, co stwierdziliśmy przed chwilą. Zatem
wbrew temu, co stwierdziliśmy przed chwilą. Zatem 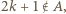 czyli (z war. (i))
czyli (z war. (i)) 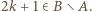
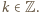 Mówią one, że
Mówią one, że 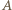 jest zbiorem wszystkich liczb parzystych, a
jest zbiorem wszystkich liczb parzystych, a 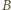 jest zbiorem wszystkich liczb nieparzystych. Ta para zbiorów spełnia, rzecz jasna, wymagane warunki - i jest to jedyna taka para.
jest zbiorem wszystkich liczb nieparzystych. Ta para zbiorów spełnia, rzecz jasna, wymagane warunki - i jest to jedyna taka para.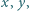 że
że 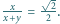 Oblicz
Oblicz 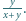
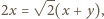 skąd otrzymujemy
skąd otrzymujemy 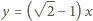 i podstawiamy:
i podstawiamy: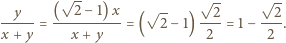
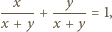
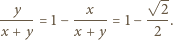
 będzie dowolną liczbą co najmniej dwucyfrową, której ostatnią cyfrą jest zero, a przedostatnią cyfrą nie jest dziewiątka. Wówczas w ciągu dwudziestu kolejnych liczb
będzie dowolną liczbą co najmniej dwucyfrową, której ostatnią cyfrą jest zero, a przedostatnią cyfrą nie jest dziewiątka. Wówczas w ciągu dwudziestu kolejnych liczb 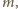
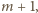 …,
…, 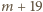 znajduje się liczba o sumie cyfr podzielnej przez 11; jeśli bowiem suma cyfr liczby
znajduje się liczba o sumie cyfr podzielnej przez 11; jeśli bowiem suma cyfr liczby  wynosi
wynosi 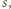 to sumy cyfr liczb
to sumy cyfr liczb 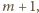 …,
…, 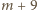 wynoszą
wynoszą 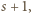 …,
…, 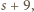 zaś liczba
zaś liczba 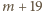 ma sumę cyfr równą
ma sumę cyfr równą 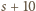 ; rzecz jasna, któraś z wartości
; rzecz jasna, któraś z wartości 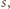
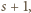 …,
…, 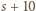 dzieli się przez 11.
dzieli się przez 11. postaci, jak wyżej.
postaci, jak wyżej.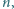 dla których równanie
dla których równanie 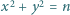 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 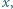
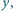 różnych od zera, ale ma rozwiązania w liczbach wymiernych
różnych od zera, ale ma rozwiązania w liczbach wymiernych 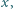
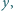 różnych od zera.
różnych od zera.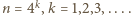 Żadna z nich nie jest sumą dwóch niezerowych kwadratów; przypuśćmy bowiem, że
Żadna z nich nie jest sumą dwóch niezerowych kwadratów; przypuśćmy bowiem, że 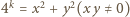 ; liczby
; liczby 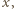
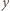 nie mogą być obie nieparzyste (bo wówczas
nie mogą być obie nieparzyste (bo wówczas 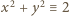 (mod 4)); muszą więc być parzyste, co daje przedstawienie liczby
(mod 4)); muszą więc być parzyste, co daje przedstawienie liczby 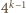 w postaci sumy dwóch niezerowych kwadratów. Dalsze zstępowanie prowadzi do konkluzji, że 4 jest sumą dwóch niezerowych kwadratów - a to absurd.
w postaci sumy dwóch niezerowych kwadratów. Dalsze zstępowanie prowadzi do konkluzji, że 4 jest sumą dwóch niezerowych kwadratów - a to absurd.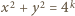 łatwo uzyskamy, biorąc dowolną trójkę pitagorejską liczb naturalnych
łatwo uzyskamy, biorąc dowolną trójkę pitagorejską liczb naturalnych 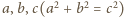 i przyjmując
i przyjmując