Zadanie ZM-1430
o zadaniu...
- Publikacja w Delcie: sierpień 2014
- Publikacja elektroniczna: 03-08-2014
Udowodnić, że dla dowolnych liczb całkowitych
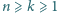 liczba
liczba

jest całkowita.
Udowodnić, że dla dowolnych liczb całkowitych
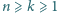 liczba
liczba

jest całkowita.
Niech
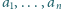 będą liczbami dodatnimi i niech
będą liczbami dodatnimi i niech
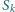 oznacza sumę
wszystkich iloczynów różnych
oznacza sumę
wszystkich iloczynów różnych
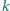 liczb spośród
liczb spośród
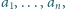
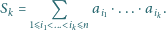
Udowodnić, że dla każdego naturalnego
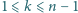 spełniona jest
nierówność
spełniona jest
nierówność
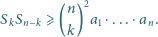
Czy, mając do dyspozycji cztery kolory, można pokolorować każdą
liczbę rzeczywistą nieujemną na jeden z nich tak, aby żadne liczby
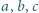 spełniające zależność
spełniające zależność
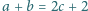 nie były tego samego
koloru?
nie były tego samego
koloru?
Czy można pokolorować każdą nieujemną liczbę rzeczywistą na czarno
lub biało tak, aby żadne trzy różne liczby
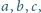 spełniające
spełniające
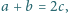 nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
Udowodnić, że jedynym rozwiązaniem równania
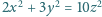 w zbiorze
liczb całkowitych jest
w zbiorze
liczb całkowitych jest
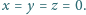
Zadanie 684 zaproponował pan Tomasz Ordowski.
Wykazać, że dla żadnej pary różnych liczb pierwszych 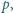
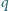 układ równań
układ równań
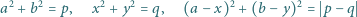
nie ma rozwiązań w liczbach całkowitych 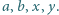
Zadanie 682 zaproponował pan Paweł Najman z Krakowa.
Liczby dodatnie 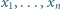 spełniają warunek
spełniają warunek
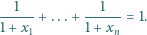
Udowodnić, że
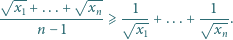
Udowodnić, że dla dodatnich liczb całkowitych
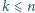 prawdziwa jest
nierówność
prawdziwa jest
nierówność
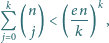
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
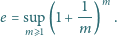
Udowodnić, że dla każdej liczby naturalnej
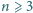 zachodzi
podzielność
zachodzi
podzielność
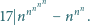
Zadanie 678 zaproponował pan Witold Bednarek z Łodzi.
Czy istnieją takie trzy różne liczby pierwsze
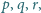 że liczba
że liczba
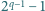 dzieli się przez
dzieli się przez
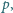 liczba
liczba
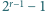 dzieli się przez
dzieli się przez
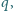 zaś liczba
zaś liczba
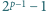 dzieli się przez
dzieli się przez
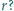
Rozważamy trójki liczb rzeczywistych
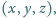 spełniające
warunki
spełniające
warunki
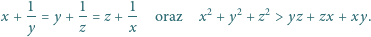 |
Wyznaczyć wszystkie możliwe wartości iloczynu
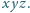
Dane są liczby rzeczywiste
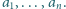 Niech
Niech
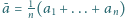 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
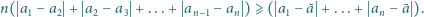 |
Udowodnić, że dowolna liczba rzeczywista
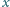 spełnia nierówność
spełnia nierówność
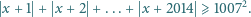 |
Czy istnieją cztery kolejne liczby całkowite dodatnie, których iloczyn,
powiększony o
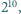 jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
Zadanie 672 zaproponował pan Witold Bednarek z Łodzi.
Wykazać, że istnieje nieskończenie wiele par liczb wymiernych dodatnich
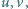 dla których liczba
dla których liczba

jest całkowita.
Zadanie 670 zaproponował pan Paweł Kubit z Krakowa.
Udowodnić nierówność
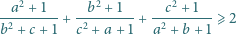
dla liczb rzeczywistych
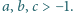
Udowodnić, że dla malejącego ciągu
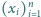 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
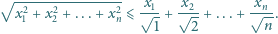 |
Dana jest liczba pierwsza
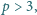 taka, że
taka, że
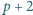 też jest pierwsza.
Na tablicy napisano liczby
też jest pierwsza.
Na tablicy napisano liczby
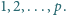 W każdym kroku wybieramy
jedną z nich, powiedzmy
W każdym kroku wybieramy
jedną z nich, powiedzmy
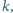 po czym zmazujemy wszystkie dzielniki
liczby
po czym zmazujemy wszystkie dzielniki
liczby
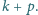 Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że dla dowolnej liczby dodatniej
 i liczby całkowitej
i liczby całkowitej
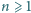 prawdziwa jest nierówność
prawdziwa jest nierówność
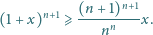 |
Udowodnić, że równanie
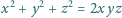
nie ma rozwiązania w liczbach całkowitych dodatnich.