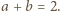Można przyjąć, że 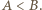 Wskażemy indukcyjną konstrukcję ciągu zbiorów
Wskażemy indukcyjną konstrukcję ciągu zbiorów 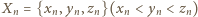 o wymaganych własnościach. Zaczniemy od trójki
o wymaganych własnościach. Zaczniemy od trójki 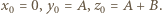 Załóżmy, że zbiory
Załóżmy, że zbiory 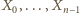 zostały już określone. Wówczas definiujemy
zostały już określone. Wówczas definiujemy 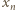 jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze
jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze 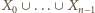 ) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg
) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg 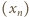 będzie rosnący.
będzie rosnący.
Aby dokończyć określenie zbioru 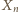 (gdy
(gdy 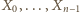 już mamy), patrzymy na liczbę
już mamy), patrzymy na liczbę 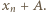 Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako
Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako 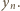 Jeżeli jest wykorzystana, bierzemy jako
Jeżeli jest wykorzystana, bierzemy jako 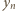 liczbę
liczbę 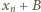 ; i z konieczności przyjmujemy
; i z konieczności przyjmujemy 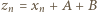 (tak więc jedna z różnic
(tak więc jedna z różnic 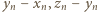 będzie równa
będzie równa 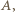 a druga
a druga 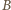 ). Tak określona liczba
). Tak określona liczba 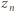 jest większa od liczb
jest większa od liczb 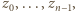 więc nie została wcześniej wykorzystana.
więc nie została wcześniej wykorzystana.
Pozostaje uzasadnić, że w przypadku, gdy liczba 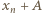 została już wykorzystana, wówczas liczba
została już wykorzystana, wówczas liczba 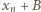 pozostała niewykorzystana (i może być użyta jako
pozostała niewykorzystana (i może być użyta jako 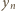 ). Przypuśćmy, że liczba
). Przypuśćmy, że liczba 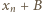 znalazła się w którymś zbiorze
znalazła się w którymś zbiorze 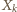 o numerze
o numerze 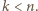 Skoro
Skoro 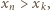 to
to 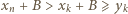 ; musiałaby zajść równość
; musiałaby zajść równość 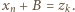 Ale
Ale 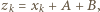 więc mielibyśmy
więc mielibyśmy 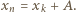 Liczba
Liczba 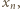 niewykorzystana aż do
niewykorzystana aż do 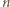 -tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru
-tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru 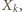 więc na mocy przyjętego algorytmu powinna była zostać użyta jako
więc na mocy przyjętego algorytmu powinna była zostać użyta jako 
Uzyskana sprzeczność dowodzi niesłuszności przypuszczenia, że 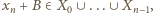 i uzasadnia poprawność określenia
i uzasadnia poprawność określenia 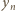 ; powstały zbiór
; powstały zbiór 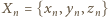 jest rozłączny ze zbiorami
jest rozłączny ze zbiorami 
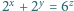 w liczbach całkowitych dodatnich
w liczbach całkowitych dodatnich 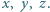
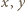 nie mogą być równe, gdyż wówczas lewa strona równania byłaby potęgą dwójki. Przyjmijmy więc, że
nie mogą być równe, gdyż wówczas lewa strona równania byłaby potęgą dwójki. Przyjmijmy więc, że 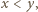 i zapiszmy
i zapiszmy 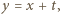 gdzie
gdzie 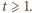 Równanie przybiera postać
Równanie przybiera postać 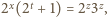 z której wynika, że
z której wynika, że 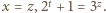
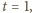 to
to 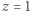 ; dostajemy rozwiązanie
; dostajemy rozwiązanie 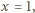
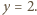
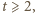 to
to 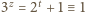 (mod 4), skąd wniosek, że
(mod 4), skąd wniosek, że  jest liczbą parzystą:
jest liczbą parzystą: 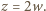 Dostajemy równanie
Dostajemy równanie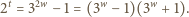
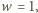 czyli
czyli 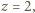
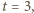 co daje rozwiązanie
co daje rozwiązanie 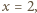
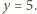
 i
i 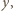 widzimy, że równanie ma cztery rozwiązania
widzimy, że równanie ma cztery rozwiązania 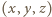 w liczbach całkowitych dodatnich:
w liczbach całkowitych dodatnich: 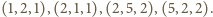
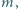 dla której istnieją takie liczby naturalne
dla której istnieją takie liczby naturalne 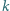 i
i 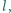 że spełnione jest równanie
że spełnione jest równanie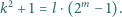
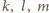 spełniają zadane równanie. Niech liczba pierwsza
spełniają zadane równanie. Niech liczba pierwsza 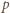 będzie nieparzystym dzielnikiem liczby
będzie nieparzystym dzielnikiem liczby 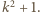 Wówczas
Wówczas 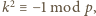 więc
więc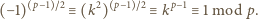
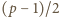 jest liczbą parzystą, czyli
jest liczbą parzystą, czyli 
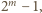 jako nieparzysty dzielnik
jako nieparzysty dzielnik 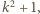 musi również dawać resztę
musi również dawać resztę 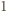 z dzielenia przez
z dzielenia przez 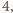 a stąd mamy
a stąd mamy 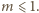
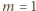 równanie jest spełnione, na przykład, przez liczby
równanie jest spełnione, na przykład, przez liczby 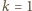 i
i 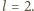
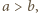 to mamy
to mamy 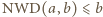 oraz
oraz 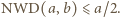 W takim razie
W takim razie 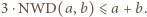 Ponieważ suma liczb na krawędziach jest równa sumie liczb w wierzchołkach, mamy
Ponieważ suma liczb na krawędziach jest równa sumie liczb w wierzchołkach, mamy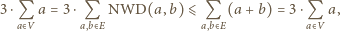
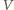 i
i 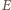 odpowiadają zbiorom wierzchołków i krawędzi dwunastościanu. Dla każdej krawędzi o końcach
odpowiadają zbiorom wierzchołków i krawędzi dwunastościanu. Dla każdej krawędzi o końcach 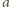 i
i 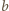 zachodzi więc równość
zachodzi więc równość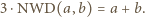
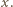 W każdym z trzech sąsiadujących z nim wierzchołków jest liczba
W każdym z trzech sąsiadujących z nim wierzchołków jest liczba 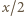 lub
lub 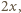 co jest sprzeczne z założeniem o przyporządkowaniu wierzchołkom parami różnych liczb.
co jest sprzeczne z założeniem o przyporządkowaniu wierzchołkom parami różnych liczb.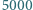 liczb
liczb 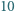 -cyfrowych podzielnych przez
-cyfrowych podzielnych przez 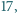 takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.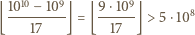
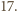 Podzielmy je na grupy - w jednej grupie znajdą się liczby złożone z jednakowych cyfr.
Podzielmy je na grupy - w jednej grupie znajdą się liczby złożone z jednakowych cyfr.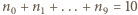 w liczbach naturalnych - liczby
w liczbach naturalnych - liczby 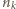 można zinterpretować jako liczby wystąpień cyfry
można zinterpretować jako liczby wystąpień cyfry 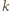 w każdym elemencie danej grupy. Rozwiązań takiego równania jest
w każdym elemencie danej grupy. Rozwiązań takiego równania jest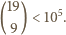
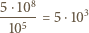
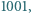 które można zapisać w postaci
które można zapisać w postaci 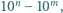 gdzie
gdzie  oraz
oraz 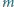 są liczbami całkowitymi spełniającymi
są liczbami całkowitymi spełniającymi 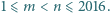
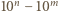 dla
dla 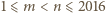 na co najwyżej jeden sposób. Stąd szukamy liczby takich par
na co najwyżej jeden sposób. Stąd szukamy liczby takich par 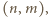 dla których liczba
dla których liczba 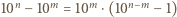 jest podzielna przez
jest podzielna przez 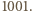 Jest to równoważne podzielności
Jest to równoważne podzielności 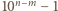 przez
przez 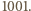
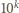 daje z dzielenia przez
daje z dzielenia przez 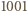 resztę
resztę 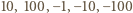 lub
lub 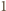 dla
dla 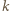 dającego z dzielenia przez
dającego z dzielenia przez 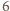 odpowiednio resztę
odpowiednio resztę 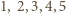 lub
lub 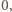 to otrzymujemy równoważność warunku z zadania z podzielnością liczby
to otrzymujemy równoważność warunku z zadania z podzielnością liczby  przez
przez 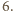 W takim razie liczby
W takim razie liczby  i
i  muszą dawać taką samą resztę z dzielenia przez
muszą dawać taką samą resztę z dzielenia przez 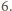
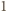 do
do 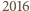 na sześć podzbiorów ze względu na resztę z dzielenia przez
na sześć podzbiorów ze względu na resztę z dzielenia przez 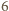 (każdy zawierający
(każdy zawierający 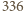 elementów). Aby wybrać liczby
elementów). Aby wybrać liczby  i
i 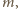 wybieramy jeden z podzbiorów, a z niego dwa elementy. Stąd szukana w zadaniu liczba to
wybieramy jeden z podzbiorów, a z niego dwa elementy. Stąd szukana w zadaniu liczba to 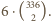
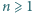 znaleźć najmniejszą liczbę rzeczywistą
znaleźć najmniejszą liczbę rzeczywistą  taką, że dla każdej liczby rzeczywistej
taką, że dla każdej liczby rzeczywistej 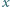 spełniona jest nierówność
spełniona jest nierówność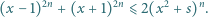
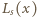 oraz
oraz 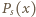 lewą oraz prawą stronę napisanej nierówności. Ponieważ
lewą oraz prawą stronę napisanej nierówności. Ponieważ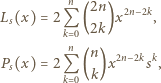
 (z parametrem
(z parametrem  )
)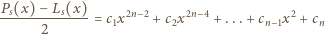
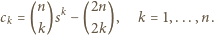
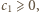 czyli
czyli 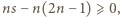 czyli
czyli 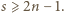
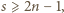 to wszystkie współczynniki
to wszystkie współczynniki 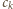 są nieujemne. Indukcja: baza
są nieujemne. Indukcja: baza 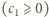 już gotowa. Ustalmy
już gotowa. Ustalmy 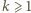 i przyjmijmy założenie indukcyjne
i przyjmijmy założenie indukcyjne 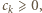 czyli
czyli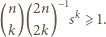
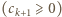 ma analogiczną postać, z
ma analogiczną postać, z 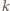 zastąpionym przez
zastąpionym przez 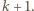 Piszemy więc to wyrażenie i zaczynamy je przekształcać:
Piszemy więc to wyrażenie i zaczynamy je przekształcać: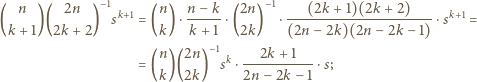
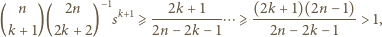
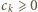 dla
dla 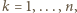 wobec czego
wobec czego 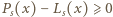 dla wszystkich
dla wszystkich 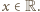
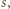 dla której
dla której 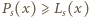 (dla
(dla 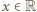 ), wynosi
), wynosi 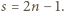
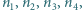 wszystkie większe od
wszystkie większe od 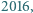 spełniające równanie
spełniające równanie
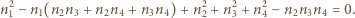
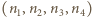 spełnia to równanie, to na mocy wzorów Viète'a spełnia je również czwórka
spełnia to równanie, to na mocy wzorów Viète'a spełnia je również czwórka 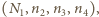 gdzie
gdzie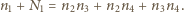
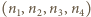 możemy uzyskać inne rozwiązanie
możemy uzyskać inne rozwiązanie 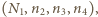 gdzie
gdzie 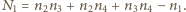 Jeśli założymy, że
Jeśli założymy, że 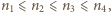 to otrzymamy
to otrzymamy 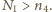 Otrzymaliśmy więc nową czwórkę liczb spełniającą równanie, przy czym minimalny element czwórki został zmieniony na element największy.
Otrzymaliśmy więc nową czwórkę liczb spełniającą równanie, przy czym minimalny element czwórki został zmieniony na element największy.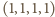 i wykonując wielokrotnie analogiczną operację, uzyskamy szukane rozwiązanie.
i wykonując wielokrotnie analogiczną operację, uzyskamy szukane rozwiązanie.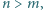 że liczby
że liczby 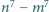 oraz
oraz 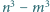 są względnie pierwsze. Wykaż, że liczby
są względnie pierwsze. Wykaż, że liczby 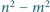 i
i 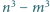 są również względnie pierwsze.
są również względnie pierwsze.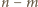 dzieli liczby względnie pierwsze
dzieli liczby względnie pierwsze 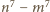 i
i 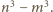 W takim razie
W takim razie 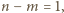 a stąd
a stąd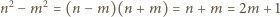
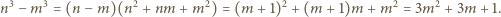
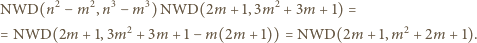
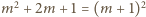 jest również dzielnikiem liczby
jest również dzielnikiem liczby 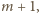 a więc także
a więc także 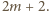 W takim razie nie może dzielić liczby
W takim razie nie może dzielić liczby 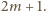 Stąd
Stąd 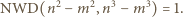
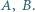 Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o
Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o 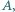 zaś od drugiej o
zaś od drugiej o 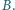
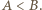 Wskażemy indukcyjną konstrukcję ciągu zbiorów
Wskażemy indukcyjną konstrukcję ciągu zbiorów 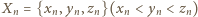 o wymaganych własnościach. Zaczniemy od trójki
o wymaganych własnościach. Zaczniemy od trójki 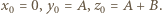 Załóżmy, że zbiory
Załóżmy, że zbiory 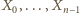 zostały już określone. Wówczas definiujemy
zostały już określone. Wówczas definiujemy 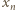 jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze
jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze 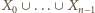 ) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg
) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg 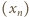 będzie rosnący.
będzie rosnący.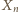 (gdy
(gdy 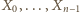 już mamy), patrzymy na liczbę
już mamy), patrzymy na liczbę 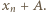 Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako
Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako 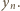 Jeżeli jest wykorzystana, bierzemy jako
Jeżeli jest wykorzystana, bierzemy jako 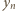 liczbę
liczbę 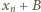 ; i z konieczności przyjmujemy
; i z konieczności przyjmujemy 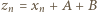 (tak więc jedna z różnic
(tak więc jedna z różnic 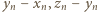 będzie równa
będzie równa 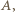 a druga
a druga 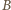 ). Tak określona liczba
). Tak określona liczba 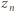 jest większa od liczb
jest większa od liczb 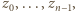 więc nie została wcześniej wykorzystana.
więc nie została wcześniej wykorzystana.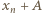 została już wykorzystana, wówczas liczba
została już wykorzystana, wówczas liczba 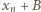 pozostała niewykorzystana (i może być użyta jako
pozostała niewykorzystana (i może być użyta jako 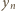 ). Przypuśćmy, że liczba
). Przypuśćmy, że liczba 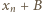 znalazła się w którymś zbiorze
znalazła się w którymś zbiorze 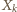 o numerze
o numerze 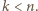 Skoro
Skoro 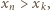 to
to 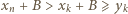 ; musiałaby zajść równość
; musiałaby zajść równość 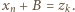 Ale
Ale 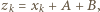 więc mielibyśmy
więc mielibyśmy 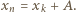 Liczba
Liczba 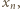 niewykorzystana aż do
niewykorzystana aż do 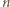 -tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru
-tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru 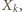 więc na mocy przyjętego algorytmu powinna była zostać użyta jako
więc na mocy przyjętego algorytmu powinna była zostać użyta jako 
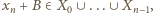 i uzasadnia poprawność określenia
i uzasadnia poprawność określenia 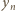 ; powstały zbiór
; powstały zbiór 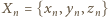 jest rozłączny ze zbiorami
jest rozłączny ze zbiorami 
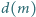 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej 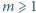
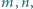 spełniających równanie
spełniających równanie 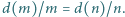
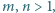 spełniających równanie
spełniających równanie 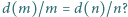
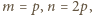 gdzie
gdzie 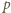 jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem
jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem 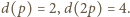
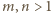 spełnia podane równanie:
spełnia podane równanie: 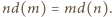 Skoro liczby
Skoro liczby 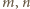 są względnie pierwsze, wynika stąd, że
są względnie pierwsze, wynika stąd, że  jest dzielnikiem liczby
jest dzielnikiem liczby 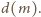 Wobec tego
Wobec tego 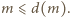 Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru
Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru 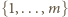 jest dzielnikiem liczby
jest dzielnikiem liczby  W szczególności
W szczególności  musi dzielić się przez
musi dzielić się przez 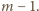 To zaś ma miejsce jedynie dla
To zaś ma miejsce jedynie dla 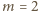 (rozważamy, z założenia, tylko
(rozważamy, z założenia, tylko 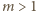 ).
).
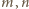 są symetryczne; to samo rozumowanie pokazuje, że także
są symetryczne; to samo rozumowanie pokazuje, że także 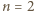 ; sprzeczność z założeniem, że
; sprzeczność z założeniem, że 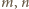 są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).
są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).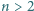 liczba
liczba 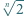 jest niewymierna.
jest niewymierna.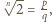 gdzie
gdzie 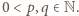 Wtedy
Wtedy 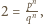 zatem
zatem 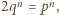 czyli
czyli 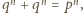 sprzecznie z Wielkim Twierdzeniem Fermata.
sprzecznie z Wielkim Twierdzeniem Fermata.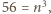 to
to 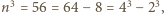 czyli
czyli 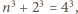 sprzecznie z Wielkim Twierdzeniem Fermata.
sprzecznie z Wielkim Twierdzeniem Fermata.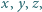 dla których
dla których 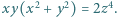
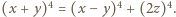 Na mocy Wielkiego Twierdzenia Fermata, skoro
Na mocy Wielkiego Twierdzenia Fermata, skoro 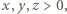 to
to 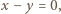 czyli
czyli 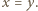 Wówczas
Wówczas 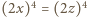 i w rezultacie
i w rezultacie 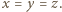
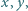 dla których
dla których 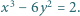
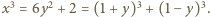 Na mocy Wielkiego Twierdzenia Fermata musi być
Na mocy Wielkiego Twierdzenia Fermata musi być 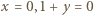 lub
lub 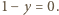 To daje rozwiązania
To daje rozwiązania 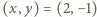 lub
lub 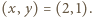
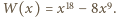 Wówczas
Wówczas 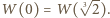 Przypuśćmy, że
Przypuśćmy, że 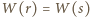 dla pewnych liczb wymiernych
dla pewnych liczb wymiernych 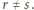 Równanie
Równanie 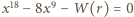 ma wtedy dwa różne pierwiastki wymierne
ma wtedy dwa różne pierwiastki wymierne 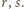 Stąd także równanie
Stąd także równanie 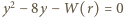 ma dwa różne pierwiastki wymierne
ma dwa różne pierwiastki wymierne 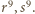 Wobec tego z wzorów Viète'a
Wobec tego z wzorów Viète'a 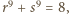 czyli
czyli 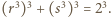
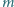 i
i  spełniają
spełniają 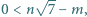 to wówczas
to wówczas 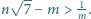
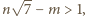 to teza jest spełniona. Ponieważ liczba
to teza jest spełniona. Ponieważ liczba 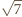 jest niewymierna, to
jest niewymierna, to 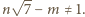 Pozostaje więc rozważyć przypadek, gdy
Pozostaje więc rozważyć przypadek, gdy 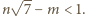 Z założenia wiemy, że
Z założenia wiemy, że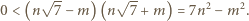
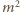 przy dzieleniu przez
przy dzieleniu przez 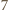 daje resztę 0, 1, 2 lub 4, więc
daje resztę 0, 1, 2 lub 4, więc 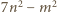 - resztę 0, 6, 5 lub 3. W takim razie
- resztę 0, 6, 5 lub 3. W takim razie 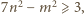 a stąd
a stąd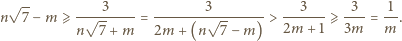
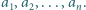 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 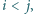 że
że 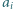 nie dzieli
nie dzieli 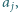 i zastąpieniu liczb
i zastąpieniu liczb 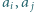 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.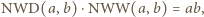 to iloczyn
to iloczyn 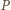 wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez
wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez 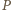 i ograniczony z dołu przez
i ograniczony z dołu przez 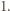 Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach
Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach 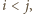 liczba
liczba 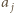 jest zamieniana na większą
jest zamieniana na większą 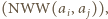 liczba
liczba 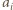 zaś - na mniejszą
zaś - na mniejszą 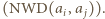 Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez
Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez 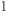 ) ani zwiększany (jako ograniczony z góry przez
) ani zwiększany (jako ograniczony z góry przez 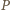 ). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.
). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.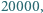 które tworzą ciąg arytmetyczny.
które tworzą ciąg arytmetyczny.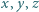 będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
będą liczbami rzeczywistymi dodatnimi. Udowodnić, że

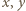 zachodzi
zachodzi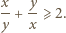
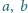 spełniają równania:
spełniają równania: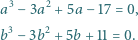
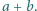
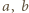 jako
jako 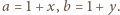 Wówczas
Wówczas
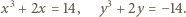
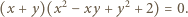
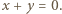 To daje odpowiedź:
To daje odpowiedź: