Klub 44M - zadania X 2020»Zadanie 807
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2020
- Publikacja w Delcie: październik 2020
- Publikacja elektroniczna: 30 września 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (373 KB)
Dane są liczby 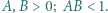 Funkcje
Funkcje 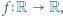
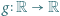 spełniają dla wszystkich
spełniają dla wszystkich 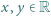 warunki
warunki
 |
przy czym 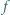 jest różnowartościowym odwzorowaniem zbioru
jest różnowartościowym odwzorowaniem zbioru 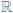 na cały zbiór
na cały zbiór 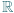 ; ma więc funkcję odwrotną
; ma więc funkcję odwrotną 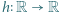
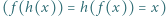 . Udowodnić, że funkcja
. Udowodnić, że funkcja 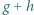 też jest różnowartościowym odwzorowaniem zbioru
też jest różnowartościowym odwzorowaniem zbioru 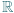 na cały zbiór
na cały zbiór 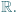
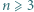 różnych liczb rzeczywistych, przy czym
różnych liczb rzeczywistych, przy czym  jest liczbą nieparzystą. Dla każdej pary
jest liczbą nieparzystą. Dla każdej pary 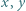 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 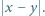 Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.
Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.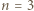 niech
niech 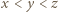 będą elementami zbioru
będą elementami zbioru 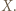 Wówczas na jednym stosie kładziemy karteczkę z liczbą
Wówczas na jednym stosie kładziemy karteczkę z liczbą 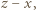 a na drugim - karteczki z liczbami
a na drugim - karteczki z liczbami 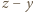 oraz
oraz 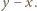
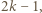 i rozważmy dowolny zbiór
i rozważmy dowolny zbiór 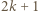 liczb
liczb 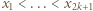 oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb
oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb 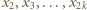 można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące
można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące 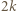 grup:
grup: 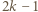 grup po dwie karteczki, z liczbami
grup po dwie karteczki, z liczbami 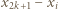 oraz
oraz 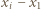 dla
dla 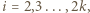 oraz jedna grupa składająca się z pozostałej karteczki z liczbą
oraz jedna grupa składająca się z pozostałej karteczki z liczbą 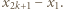 Zauważmy, że w każdej grupie suma liczb z karteczek jest równa
Zauważmy, że w każdej grupie suma liczb z karteczek jest równa 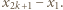 Wobec tego wystarczy karteczki z dowolnych
Wobec tego wystarczy karteczki z dowolnych 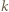 grup dołączyć do jednego stosu, a karteczki z pozostałych
grup dołączyć do jednego stosu, a karteczki z pozostałych 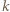 grup - do drugiego stosu. To kończy dowód indukcyjny.
grup - do drugiego stosu. To kończy dowód indukcyjny.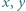 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 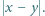 Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?
Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?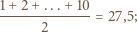
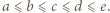 Wówczas najmniejsza z liczb zapisanych na karteczkach to
Wówczas najmniejsza z liczb zapisanych na karteczkach to 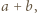 druga najmniejsza (być może równa) -
druga najmniejsza (być może równa) - 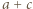 ; największa to
; największa to  a druga największa -
a druga największa - 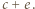 Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy
Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy 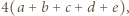 a zatem znamy również wartość
a zatem znamy również wartość 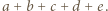 Ta wiedza wystarcza kolejno do znalezienia wartości
Ta wiedza wystarcza kolejno do znalezienia wartości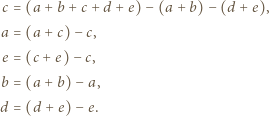
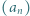 jest określony wzorami
jest określony wzorami 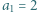 ;
; 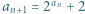 dla
dla 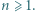 Niech
Niech 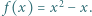 Udowodnić, że dla każdego
Udowodnić, że dla każdego 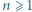 liczba
liczba 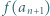 dzieli się przez
dzieli się przez 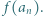
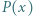 będzie wielomianem
będzie wielomianem 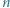 -tego stopnia
-tego stopnia 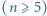 o współczynnikach całkowitych, mającym
o współczynnikach całkowitych, mającym 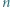 różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian
różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian 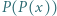 również ma dokładnie
również ma dokładnie  różnych pierwiastków całkowitych.
różnych pierwiastków całkowitych.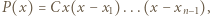 gdzie
gdzie 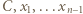 są liczbami całkowitymi. Oczywiście
są liczbami całkowitymi. Oczywiście 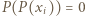 dla
dla 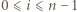 (przyjmujemy
(przyjmujemy 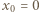 ). Załóżmy, że
). Załóżmy, że 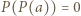 dla pewnego
dla pewnego 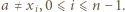 Wówczas
Wówczas 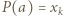 dla pewnego
dla pewnego 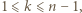 czyli
czyli 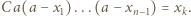 W tej sytuacji
W tej sytuacji 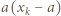 dzieli
dzieli 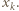 Załóżmy, że
Załóżmy, że 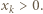 Z podzielności
Z podzielności 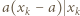 wnioskujemy kolejno
wnioskujemy kolejno 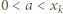 oraz
oraz 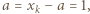 czyli
czyli 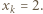 Jednak
Jednak 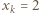 ma tylko 4 różne dzielniki całkowite, co przeczy równości
ma tylko 4 różne dzielniki całkowite, co przeczy równości 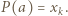 Przypadek
Przypadek 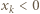 rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu
rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu 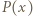 są całkowitymi pierwiastkami wielomianu
są całkowitymi pierwiastkami wielomianu 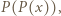 co dopełnia rozwiązanie.
co dopełnia rozwiązanie.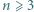 istnieją nieparzyste liczby
istnieją nieparzyste liczby 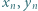 spełniające równanie
spełniające równanie 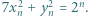
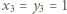 spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby
spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby 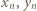 spełniają
spełniają 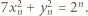 Wówczas
Wówczas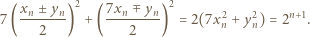
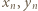 są nieparzyste, to jedna z par
są nieparzyste, to jedna z par 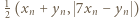 oraz
oraz 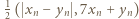 składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako
składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako 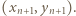 W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej
W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej 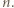
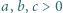 spełniają warunek
spełniają warunek 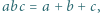 to
to 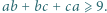
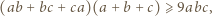
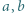 i
i  spełniają równość
spełniają równość 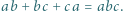 Dowieść, że
Dowieść, że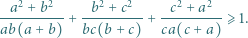
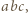 a prawą przez
a prawą przez 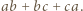 Następnie skorzystać z nierówności
Następnie skorzystać z nierówności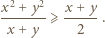
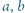 i
i  spełniają warunek
spełniają warunek 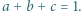 Dowieść, że
Dowieść, że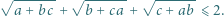
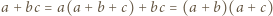 wraz z dwiema analogicznymi równościami. Wykorzystać nierówność
wraz z dwiema analogicznymi równościami. Wykorzystać nierówność 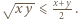
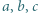 jest równy 1, to
jest równy 1, to 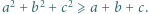
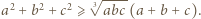 Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną
Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną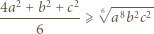
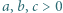 prawdziwa jest nierówność
prawdziwa jest nierówność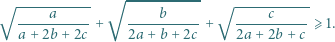
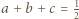 i udowodnić, że
i udowodnić, że 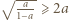 dla
dla 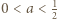 oraz analogicznie dla
oraz analogicznie dla 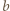 i
i 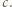
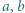 i
i  oraz liczby całkowitej
oraz liczby całkowitej 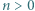 zachodzi nierówność
zachodzi nierówność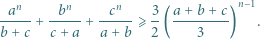
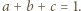 Wtedy
Wtedy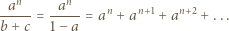
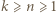 z nierówności
z nierówności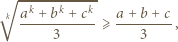
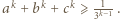 Tę ostatnią nierówność wystarczy zsumować dla
Tę ostatnią nierówność wystarczy zsumować dla 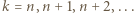
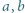 i
i  oraz liczby całkowitej
oraz liczby całkowitej 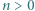 zachodzi nierówność
zachodzi nierówność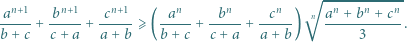
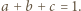 Posługując się nierównościami między średnimi potęgowymi, wykazać dla
Posługując się nierównościami między średnimi potęgowymi, wykazać dla 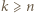 nierówności
nierówności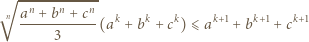
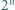 jedynek ma co najmniej
jedynek ma co najmniej 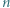 różnych dzielników pierwszych.
różnych dzielników pierwszych.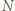 będzie liczbą składającą się w zapisie dziesiętnym z
będzie liczbą składającą się w zapisie dziesiętnym z 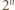 jedynek. Mamy
jedynek. Mamy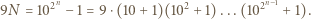
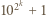 i
i 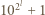 są względnie pierwsze dla
są względnie pierwsze dla 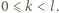 Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą
Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 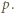 Oczywiście liczba
Oczywiście liczba 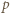 jest nieparzysta. Ponieważ
jest nieparzysta. Ponieważ 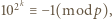 więc
więc 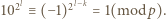 Skoro jednak
Skoro jednak 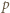 dzieli
dzieli 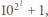 to
to 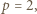 co przeczy wcześniej poczynionej uwadze o nieparzystości
co przeczy wcześniej poczynionej uwadze o nieparzystości 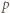 i kończy rozwiązanie zadania.
i kończy rozwiązanie zadania.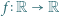 spełniające dla wszystkich
spełniające dla wszystkich 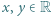 nierówność
nierówność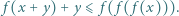
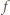 spełnia warunki zadania. Niech
spełnia warunki zadania. Niech 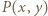 oznacza nierówność
oznacza nierówność 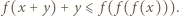 Wybierzmy dowolnie
Wybierzmy dowolnie 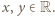 Ponieważ
Ponieważ 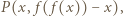 więc
więc 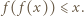 Podstawiając w ostatniej nierówności
Podstawiając w ostatniej nierówności 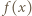 zamiast
zamiast  i uwzględniając
i uwzględniając 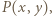 dostajemy
dostajemy 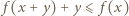 dla dowolnych
dla dowolnych 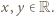 Podstawiając
Podstawiając 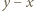 zamiast
zamiast 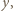 dostajemy
dostajemy 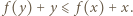 Z dowolności
Z dowolności 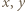 wnioskujemy, że
wnioskujemy, że 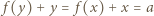 dla pewnego
dla pewnego 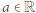 i wszystkich
i wszystkich 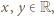 zatem musi być
zatem musi być 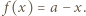 Łatwo sprawdzić, że ta funkcja faktycznie spełnia
Łatwo sprawdzić, że ta funkcja faktycznie spełnia 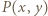 dla wszystkich
dla wszystkich 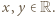
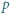
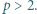

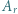
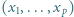
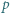 ), że
), że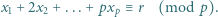
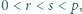

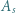
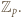
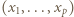


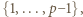
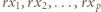
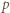
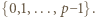
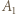 - czyli spełniała zależność
- czyli spełniała zależność 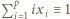 (mod
(mod 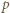 ) - to po pomnożeniu wszystkich jej wyrazów przez
) - to po pomnożeniu wszystkich jej wyrazów przez 
 - czyli permutację należącą do zbioru
- czyli permutację należącą do zbioru 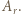
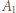
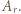
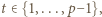
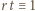 (mod
(mod 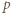 ) (taki element
) (taki element 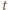
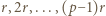
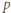
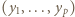
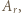
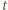
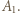
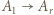 (mnożenie przez
(mnożenie przez  ) oraz
) oraz 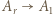 (mnożenie przez
(mnożenie przez 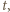
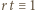 ) są wzajemnie odwrotne. To dowodzi, że zbiór
) są wzajemnie odwrotne. To dowodzi, że zbiór 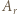
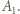
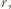
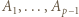
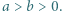
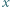
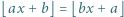 zawiera pewien przedział długości
zawiera pewien przedział długości 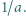
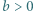
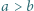
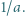
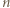
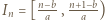
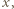
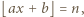
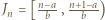
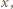
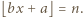
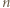
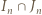
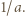
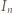
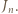
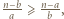
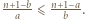 Po prostym przekształceniu ta koniunkcja przybiera postać
Po prostym przekształceniu ta koniunkcja przybiera postać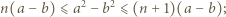
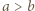
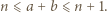
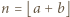
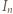
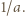
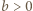
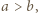
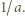
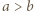
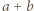
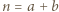
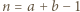
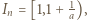
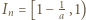 ; i
; i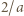 ; więc większej niż
; więc większej niż 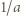 ; a
; a taką, że liczby
taką, że liczby 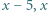 oraz
oraz 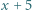 są kwadratami.
są kwadratami.