Eksperymenty z niewielkimi wartościami
 pozwalają zgadnąć, że
szukaną wielokrotnością liczby
pozwalają zgadnąć, że
szukaną wielokrotnością liczby
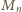 jest iloczyn
jest iloczyn
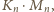 gdzie
gdzie
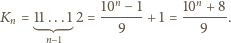
Rzeczywiście, iloczyn
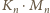 nie ma dziewiątki w zapisie dziesiętnym:
nie ma dziewiątki w zapisie dziesiętnym:
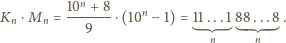
Należy teraz wykazać, że dziewiątka występuje w każdym z iloczynów
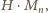 gdy
gdy
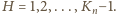
Niech
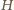 będzie liczbą
będzie liczbą
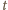 -cyfrową:
-cyfrową:
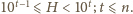 Bierzemy
iloczyn
Bierzemy
iloczyn
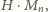 skreślamy jego końcowe
skreślamy jego końcowe
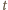 cyfr i dostajemy
liczbę
cyfr i dostajemy
liczbę
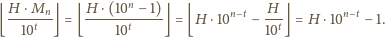
Jeżeli
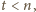 uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
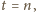 zaś
zaś
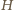 kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
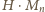 ma dziewiątkę w rzędzie
ma dziewiątkę w rzędzie
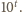
Pamiętając, że rozważamy
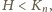 pozostaje rozpatrzeć sytuacje,
gdy
pozostaje rozpatrzeć sytuacje,
gdy
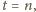 przy czym albo
przy czym albo
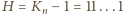 (wówczas
(wówczas
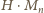 ma dziewiątkę na końcu), albo
ma dziewiątkę na końcu), albo
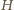 ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
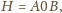 gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
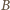 jest grupą
jest grupą
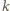 -cyfrową; oczywiście
-cyfrową; oczywiście
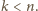 W myśl rozpatrzonego już przypadku, iloczyn
W myśl rozpatrzonego już przypadku, iloczyn
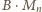 ma
dziewiątkę w rzędzie
ma
dziewiątkę w rzędzie
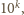 czyli właśnie na tej pozycji, na której
czyli właśnie na tej pozycji, na której
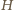 ma zero. Ta dziewiątka pozostanie obecna w iloczynie
ma zero. Ta dziewiątka pozostanie obecna w iloczynie
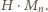
Zatem, istotnie,
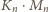 jest najmniejszą wielokrotnością liczby
jest najmniejszą wielokrotnością liczby
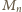 bez dziewiątki w zapisie dziesiętnym.
bez dziewiątki w zapisie dziesiętnym.
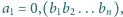 w której zapisie
dziesiętnym blok cyfr
w której zapisie
dziesiętnym blok cyfr
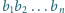 powtarza się okresowo po przecinku.
Rozważmy liczby
powtarza się okresowo po przecinku.
Rozważmy liczby
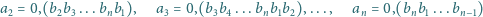
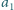 przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
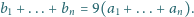
 dla
dla
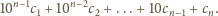
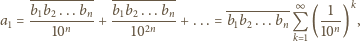
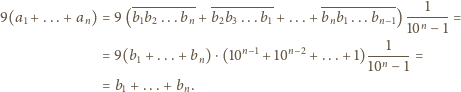
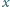 spełnia równanie
spełnia równanie
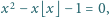 to każda potęga liczby
to każda potęga liczby
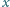 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
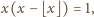 to
to
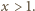 Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
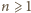 różnica
różnica
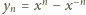 jest liczbą
całkowitą.
jest liczbą
całkowitą.
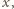 widzimy, że
widzimy, że
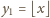 (liczba całkowita). Zatem także liczba
(liczba całkowita). Zatem także liczba
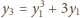 jest całkowita.
jest całkowita.
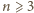 i załóżmy, że liczby
i załóżmy, że liczby
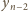 oraz
oraz
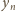 są całkowite. Przekształcenie
są całkowite. Przekształcenie
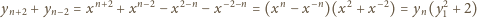
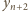 też jest całkowita. Przez indukcję
wnosimy, że liczby
też jest całkowita. Przez indukcję
wnosimy, że liczby
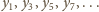 wszystkie są całkowite.
wszystkie są całkowite.
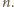 Ze związków
Ze związków
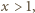
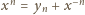 (
(
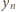 całkowite) wynika, że
całkowite) wynika, że
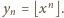 Zachodzi
więc równość
Zachodzi
więc równość
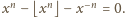 Wystarczy ją pomnożyć przez
Wystarczy ją pomnożyć przez
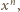 by uzyskać tezę zadania.
by uzyskać tezę zadania.
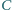 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
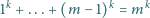
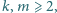 to
to
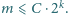
 nie może być zbyt duże. Do dziś pozostaje
otwartym problemem hipoteza Erdősa, że to równanie nie ma rozwiązań
(zob. również zadanie M 1374, Delta 1(464)/2013).
nie może być zbyt duże. Do dziś pozostaje
otwartym problemem hipoteza Erdősa, że to równanie nie ma rozwiązań
(zob. również zadanie M 1374, Delta 1(464)/2013).
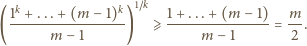
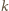 i
i
 spełniają podane równanie, dostajemy
spełniają podane równanie, dostajemy
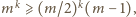 a stąd
a stąd
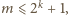 co jest mniejsze niż
co jest mniejsze niż
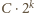 np. dla
np. dla
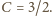
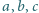 jest spełniona
nierówność
jest spełniona
nierówność
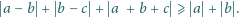
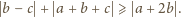
 i wystarczy teraz udowodnić,
że
i wystarczy teraz udowodnić,
że
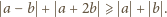
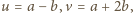 tzn.
tzn.
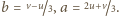 Otrzymujemy wówczas
Otrzymujemy wówczas
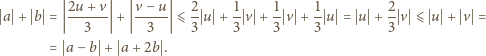
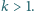 Znaleźć wszystkie liczby naturalne
Znaleźć wszystkie liczby naturalne
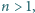 spełniające nierówność
spełniające nierówność

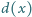 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej

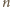 ma co najmniej dwa różne dzielniki pierwsze
ma co najmniej dwa różne dzielniki pierwsze
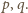 Napiszmy
Napiszmy
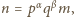 gdzie
gdzie
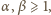 zaś czynnik
zaś czynnik
 jest niepodzielny przez
jest niepodzielny przez
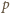 ani
ani
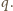 Iloczyn
Iloczyn
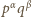 ma
ma
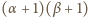 dzielników dodatnich; iloczyn
dzielników dodatnich; iloczyn
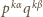 ma
ma
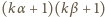 dzielników dodatnich. Zatem
dzielników dodatnich. Zatem
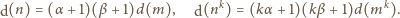
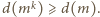 Jeśli więc zachodzi postulowana nierówność
Jeśli więc zachodzi postulowana nierówność
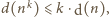 to
to
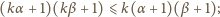
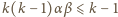 ; a to jest niemożliwe, skoro
; a to jest niemożliwe, skoro
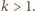
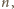 będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
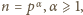 to
to
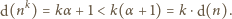

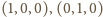 i
i
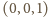 oraz sferę o środku w punkcie
oraz sferę o środku w punkcie
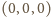 i promieniu 1. Sfera ta przechodzi przez te same trzy punkty, więc
przecina się z daną płaszczyzną wzdłuż okręgu przez nie wyznaczonego. Stąd
układ równań ma nieskończenie wiele rozwiązań.
i promieniu 1. Sfera ta przechodzi przez te same trzy punkty, więc
przecina się z daną płaszczyzną wzdłuż okręgu przez nie wyznaczonego. Stąd
układ równań ma nieskończenie wiele rozwiązań.

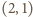 i promieniu
i promieniu
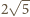 oraz
okrąg o środku
oraz
okrąg o środku
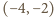 i promieniu
i promieniu
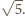 Odległość między
środkami tych okręgów równa jest
Odległość między
środkami tych okręgów równa jest
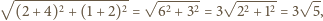
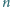 i liczby całkowite dodatnie względnie
pierwsze
i liczby całkowite dodatnie względnie
pierwsze
 i
i
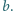 Udowodnić, że liczba
Udowodnić, że liczba
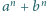 jest
podzielna przez
jest
podzielna przez
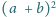 wtedy i tylko wtedy, gdy liczba
wtedy i tylko wtedy, gdy liczba
 jest
podzielna przez
jest
podzielna przez
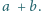
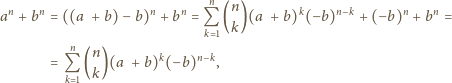
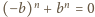 dla nieparzystych
dla nieparzystych
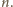 Zatem
Zatem
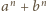 przy dzieleniu przez
przy dzieleniu przez
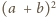 daje taką samą resztę jak
składnik odpowiadający
daje taką samą resztę jak
składnik odpowiadający
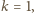 który wynosi
który wynosi
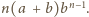 Zatem
Zatem
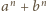 jest podzielne przez
jest podzielne przez
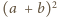 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
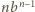 jest podzielne przez
jest podzielne przez
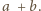 Ponieważ
Ponieważ
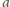 i
i
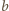 są
względnie pierwsze, względnie pierwsze są również
są
względnie pierwsze, względnie pierwsze są również
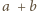 i
i
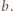 Stąd
otrzymujemy tezę.
Stąd
otrzymujemy tezę.
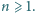 Niech
Niech
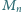 będzie liczbą
naturalną, której zapis dziesiętny składa się z
będzie liczbą
naturalną, której zapis dziesiętny składa się z
 dziewiątek:
dziewiątek:
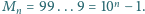 Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
 pozwalają zgadnąć, że
szukaną wielokrotnością liczby
pozwalają zgadnąć, że
szukaną wielokrotnością liczby
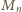 jest iloczyn
jest iloczyn
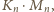 gdzie
gdzie
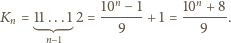
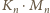 nie ma dziewiątki w zapisie dziesiętnym:
nie ma dziewiątki w zapisie dziesiętnym:
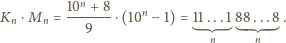
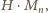 gdy
gdy
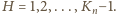
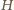 będzie liczbą
będzie liczbą
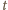 -cyfrową:
-cyfrową:
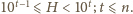 Bierzemy
iloczyn
Bierzemy
iloczyn
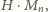 skreślamy jego końcowe
skreślamy jego końcowe
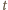 cyfr i dostajemy
liczbę
cyfr i dostajemy
liczbę
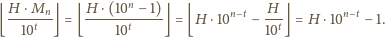
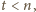 uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
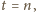 zaś
zaś
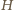 kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
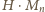 ma dziewiątkę w rzędzie
ma dziewiątkę w rzędzie
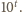
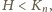 pozostaje rozpatrzeć sytuacje,
gdy
pozostaje rozpatrzeć sytuacje,
gdy
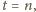 przy czym albo
przy czym albo
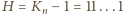 (wówczas
(wówczas
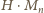 ma dziewiątkę na końcu), albo
ma dziewiątkę na końcu), albo
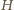 ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
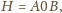 gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
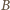 jest grupą
jest grupą
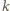 -cyfrową; oczywiście
-cyfrową; oczywiście
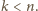 W myśl rozpatrzonego już przypadku, iloczyn
W myśl rozpatrzonego już przypadku, iloczyn
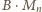 ma
dziewiątkę w rzędzie
ma
dziewiątkę w rzędzie
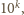 czyli właśnie na tej pozycji, na której
czyli właśnie na tej pozycji, na której
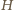 ma zero. Ta dziewiątka pozostanie obecna w iloczynie
ma zero. Ta dziewiątka pozostanie obecna w iloczynie
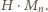
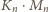 jest najmniejszą wielokrotnością liczby
jest najmniejszą wielokrotnością liczby
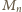 bez dziewiątki w zapisie dziesiętnym.
bez dziewiątki w zapisie dziesiętnym.
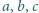 jest nie mniejsza od
jest nie mniejsza od
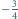 oraz
oraz
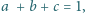 to
to

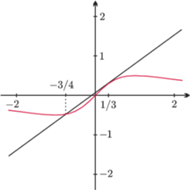
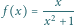
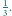
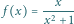
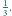
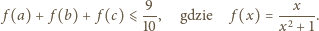
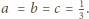 Równanie
stycznej do funkcji
Równanie
stycznej do funkcji
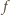 w punkcie
w punkcie
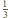 ma postać
ma postać
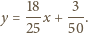
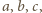 spełniających warunek
spełniających warunek
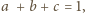 suma wartości wyrażenia
suma wartości wyrażenia
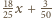 jest równa
jest równa
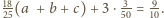
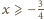 prawdziwa jest
nierówność
prawdziwa jest
nierówność
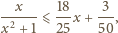
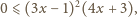
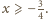
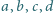 zachodzi
nierówność
zachodzi
nierówność

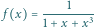
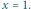
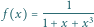
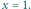
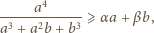
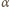 i
i
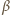 są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
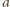 i podstawiając
i podstawiając
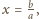 otrzymujemy
otrzymujemy
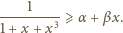
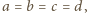 więc musimy tak dobrać współczynniki
więc musimy tak dobrać współczynniki
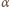 i
i
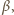 aby równość zachodziła dla
aby równość zachodziła dla
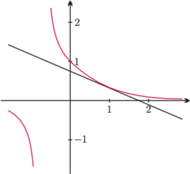
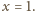 Znajdując
równanie stycznej do wykresu funkcji
Znajdując
równanie stycznej do wykresu funkcji
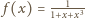 w punkcie
w punkcie
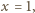 otrzymujemy współczynniki
otrzymujemy współczynniki
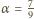 i
i
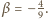
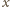 zachodzi
nierówność
zachodzi
nierówność
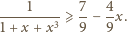
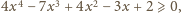 a następnie
doprowadzamy nierówność do postaci
a następnie
doprowadzamy nierówność do postaci
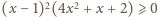 – teraz
widać, że to prawda dla dowolnego
– teraz
widać, że to prawda dla dowolnego
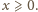
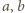 zachodzi nierówność
zachodzi nierówność
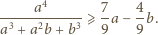
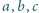 zachodzi
nierówność
zachodzi
nierówność

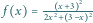
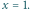
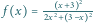
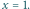
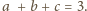 (Jest to bardziej wygodne niż założenie
(Jest to bardziej wygodne niż założenie
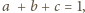 gdyż
równość zachodzi dla
gdyż
równość zachodzi dla
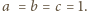 ) Wówczas dana nierówność
przyjmuje postać
) Wówczas dana nierówność
przyjmuje postać
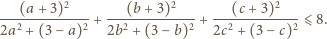
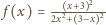 w punkcie
w punkcie
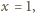 otrzymujemy do udowodnienia nierówność
otrzymujemy do udowodnienia nierówność
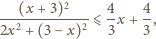
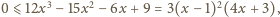 co
jest prawdą dla
co
jest prawdą dla
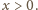
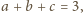 nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
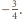
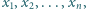 gdzie
gdzie
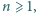 spełniają warunki
spełniają warunki

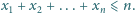
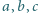 zachodzi
nierówność
zachodzi
nierówność

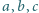 zachodzi
nierówność
zachodzi
nierówność

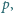 dla której
dla której
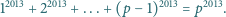
 zachodzi
zachodzi
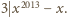 Stąd
Stąd
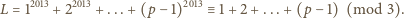
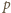 jest postaci
jest postaci
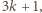 to wówczas
to wówczas
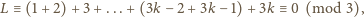
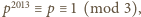 więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
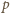 postaci
postaci
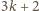 równanie jest sprzeczne. Zatem jedyna możliwość to
równanie jest sprzeczne. Zatem jedyna możliwość to
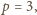 ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
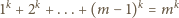
 oraz
oraz
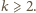 Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
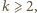 to
to
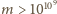 (zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
(zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
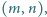 dla których
liczby
dla których
liczby

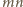 powinien być dzielnikiem liczb
powinien być dzielnikiem liczb
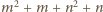 oraz
oraz
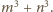 Zatem
Zatem
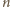 ma być dzielnikiem liczb
ma być dzielnikiem liczb
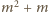 oraz
oraz
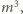 więc także liczby
więc także liczby
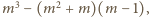 równej
równej
 Przez symetrię, liczba
Przez symetrię, liczba
 ma być dzielnikiem liczby
ma być dzielnikiem liczby
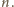 Dostajemy warunek
Dostajemy warunek
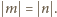
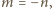 podane w zadaniu sumy wynoszą
podane w zadaniu sumy wynoszą
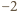 oraz 0
(więc są całkowite). Jeśli zaś
oraz 0
(więc są całkowite). Jeśli zaś
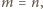 wynoszą one odpowiednio
wynoszą one odpowiednio
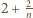 oraz
oraz
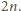 Są one obie całkowite wtedy i tylko wtedy, gdy
Są one obie całkowite wtedy i tylko wtedy, gdy
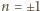 lub
lub
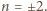
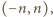 gdzie
gdzie
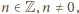 a ponadto cztery pary
a ponadto cztery pary
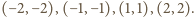
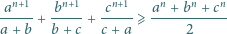
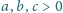 oraz liczb całkowitych
oraz liczb całkowitych
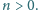
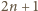 liczb, mianowicie
liczb, mianowicie
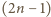 -krotnie powtórzonej liczby
-krotnie powtórzonej liczby
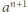 oraz liczb
oraz liczb
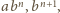 jest nie mniejsza od ich średniej geometrycznej, równej
jest nie mniejsza od ich średniej geometrycznej, równej
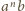 :
:
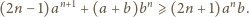
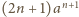 i po prostym przekształceniu
otrzymujemy
i po prostym przekształceniu
otrzymujemy
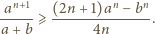
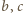 oraz
oraz
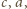 po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
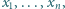 które są nie mniejsze niż
które są nie mniejsze niż
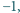 spełniają
równość
spełniają
równość
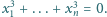 Udowodnić, że
Udowodnić, że
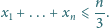
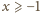 zachodzi
zachodzi
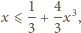
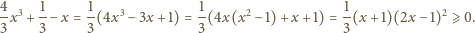
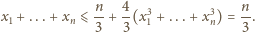

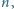 dla których kwadrat
złożony z
dla których kwadrat
złożony z
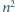 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
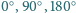 lub
lub
 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

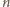 jest
podzielne przez
jest
podzielne przez
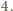
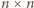 udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
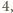 to
to
 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
 Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
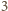 czarne pola
lub
czarne pola
lub
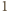 czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
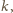 a drugiego
a drugiego
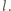 Zliczając czarne i białe pola, otrzymujemy
Zliczając czarne i białe pola, otrzymujemy
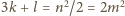 oraz
oraz
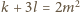 (dzięki temu, że
(dzięki temu, że
 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
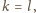 więc
więc
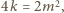 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
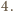
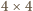 spełniające
warunki zadania, więc także dowolnego kwadratu
spełniające
warunki zadania, więc także dowolnego kwadratu
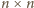 dla
dla
 będącego wielokrotnością
będącego wielokrotnością