Podstawmy, kolejno, 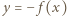 oraz
oraz 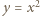 ; otrzymujemy równania
; otrzymujemy równania
oraz
które po dodaniu stronami i redukcji dają związek 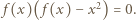 Zatem dla każdej liczby
Zatem dla każdej liczby 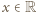 ma miejsce alternatywa:
ma miejsce alternatywa: 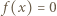 lub
lub 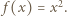 Stąd, w szczególności,
Stąd, w szczególności, 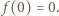
Jeśli 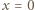 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 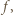 to
to 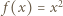 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 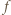 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 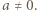 Wykażemy, że wówczas
Wykażemy, że wówczas 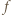 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.
Przypuśćmy, że 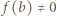 dla pewnego
dla pewnego 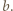 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 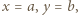 dostajemy
dostajemy 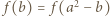 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 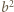 oraz
oraz 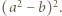 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 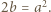 To liczba dodatnia; stąd
To liczba dodatnia; stąd 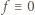 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 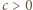 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 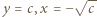 (już wiemy, że
(już wiemy, że 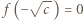 ). Wychodzi
). Wychodzi 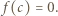 Tak więc
Tak więc 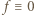 także w przedziale
także w przedziale 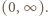
Wniosek (odpowiedź): jedynymi funkcjami spełniającymi podane równanie są: 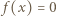 (dla wszystkich
(dla wszystkich 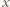 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).
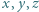 spełniają równość
spełniają równość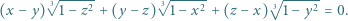
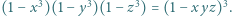
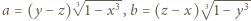 i
i 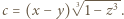 Następnie zauważyć, że
Następnie zauważyć, że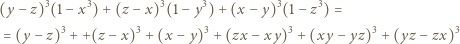
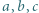 spełniają równość
spełniają równość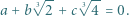
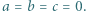
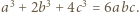 Wykazać kolejno, że
Wykazać kolejno, że 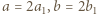 i
i 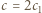 dla pewnych całkowitych
dla pewnych całkowitych 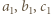 i zauważyć, że
i zauważyć, że 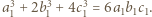 Następnie to samo rozumowanie zastosować do
Następnie to samo rozumowanie zastosować do 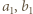 i
i 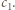 Ten proces można kontynuować w nieskończoność, co dowodzi, że każda potęga dwójki dzieli
Ten proces można kontynuować w nieskończoność, co dowodzi, że każda potęga dwójki dzieli 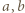 i
i 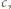 czyli
czyli 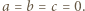
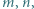 przy czym
przy czym 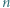 jest liczbą nieparzystą, większą niż
jest liczbą nieparzystą, większą niż 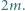 Udowodnić, że liczba
Udowodnić, że liczba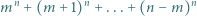
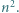
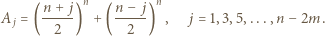
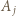 dzieli się przez
dzieli się przez 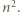 W rozwinięciu dwumianowym
W rozwinięciu dwumianowym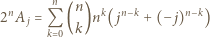
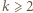 są podzielne przez
są podzielne przez 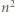 ; skoro zaś
; skoro zaś 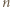 jest liczbą nieparzystą, dwa składniki początkowe dają w sumie
jest liczbą nieparzystą, dwa składniki początkowe dają w sumie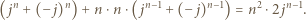
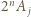 dzieli się przez
dzieli się przez 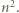 Korzystając jeszcze raz z nieparzystości
Korzystając jeszcze raz z nieparzystości 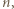 wnosimy, że
wnosimy, że 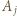 dzieli się przez
dzieli się przez 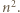
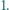 Jeśli na tablicy napisana jest co najmniej jedna z liczb
Jeśli na tablicy napisana jest co najmniej jedna z liczb 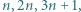 to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.
to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.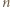 mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.
mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.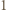 z dzielenia przez
z dzielenia przez 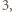 powiedzmy
powiedzmy 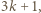 można uzyskać w jednym kroku z liczby
można uzyskać w jednym kroku z liczby 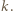 Liczba dająca resztę
Liczba dająca resztę 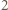 z dzielenia przez
z dzielenia przez 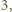 powiedzmy
powiedzmy 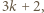 może zostać uzyskana w dwóch krokach z liczby
może zostać uzyskana w dwóch krokach z liczby 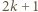 : w pierwszym kroku dopisujemy liczbę
: w pierwszym kroku dopisujemy liczbę 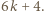 Wreszcie liczba podzielna przez
Wreszcie liczba podzielna przez 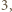 powiedzmy
powiedzmy 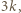 może zostać uzyskana w siedmiu krokach z liczby
może zostać uzyskana w siedmiu krokach z liczby 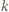 : w kolejnych pośrednich krokach dopisujemy
: w kolejnych pośrednich krokach dopisujemy 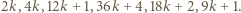
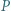 o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.
o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.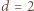 wywnioskujemy, że
wywnioskujemy, że 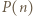 jest liczbą nieparzystą dla każdego całkowitego
jest liczbą nieparzystą dla każdego całkowitego 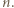
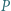 o współczynnikach całkowitych przyjmuje wartość
o współczynnikach całkowitych przyjmuje wartość 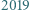 dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.
dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.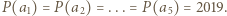 Liczby
Liczby 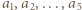 są różnymi pierwiastkami wielomianu
są różnymi pierwiastkami wielomianu 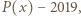 więc na mocy twierdzenia Bézouta
więc na mocy twierdzenia Bézouta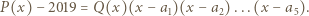
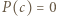 dla pewnego całkowitego
dla pewnego całkowitego 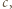 to liczba
to liczba 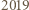 byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.
byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.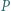 o współczynnikach całkowitych ma tę własność, że
o współczynnikach całkowitych ma tę własność, że 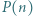 jest liczbą pierwszą dla wszystkich naturalnych
jest liczbą pierwszą dla wszystkich naturalnych 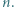 Dowieść, że
Dowieść, że 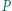 jest wielomianem stałym.
jest wielomianem stałym.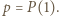 Na mocy twierdzenia
Na mocy twierdzenia 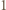 dla naturalnych
dla naturalnych 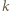 mamy
mamy 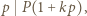 więc
więc 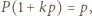 gdyż wartości
gdyż wartości 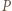 dla argumentów całkowitych są liczbami pierwszymi. Wielomian
dla argumentów całkowitych są liczbami pierwszymi. Wielomian 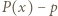 ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.
ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.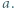 Niech
Niech 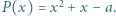 Udowodnić, że jeśli dla pewnego naturalnego
Udowodnić, że jeśli dla pewnego naturalnego 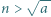 liczby
liczby 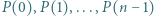 są względne pierwsze z
są względne pierwsze z 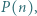 to liczba
to liczba 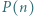 jest pierwsza.
jest pierwsza.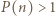 dla
dla 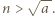 Przypuśćmy, że liczba
Przypuśćmy, że liczba 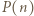 nie jest pierwsza. Wtedy ma ona dzielnik pierwszy
nie jest pierwsza. Wtedy ma ona dzielnik pierwszy 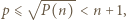 czyli
czyli 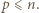 Wówczas
Wówczas 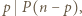 czyli
czyli 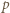 jest wspólnym dzielnikiem
jest wspólnym dzielnikiem 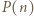 i
i 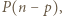 a to jest sprzeczne z założeniami.
a to jest sprzeczne z założeniami.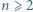 o następującej własności: Liczby całkowite od
o następującej własności: Liczby całkowite od 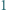 do
do 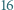 można tak wpisać w pola tablicy
można tak wpisać w pola tablicy 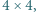 aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez
aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez 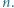
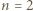 oraz
oraz 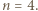
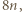 a z drugiej - nie większa od
a z drugiej - nie większa od 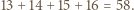 Stąd wniosek, że
Stąd wniosek, że 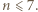 Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli
Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli 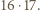 Liczba
Liczba 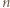 jest dzielnikiem tej sumy, wobec czego
jest dzielnikiem tej sumy, wobec czego 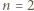 lub
lub 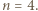 Poniższy przykład pozwala stwierdzić, że te wartości
Poniższy przykład pozwala stwierdzić, że te wartości 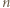 w istocie są osiągalne.
w istocie są osiągalne.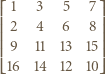
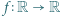 spełniające równanie
spełniające równanie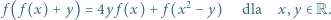
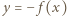 oraz
oraz 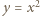 ; otrzymujemy równania
; otrzymujemy równania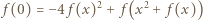
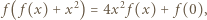
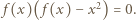 Zatem dla każdej liczby
Zatem dla każdej liczby 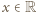 ma miejsce alternatywa:
ma miejsce alternatywa: 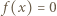 lub
lub 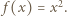 Stąd, w szczególności,
Stąd, w szczególności, 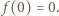
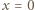 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 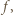 to
to 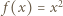 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 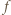 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 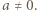 Wykażemy, że wówczas
Wykażemy, że wówczas 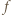 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.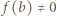 dla pewnego
dla pewnego 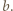 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 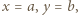 dostajemy
dostajemy 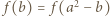 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 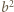 oraz
oraz 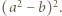 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 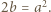 To liczba dodatnia; stąd
To liczba dodatnia; stąd 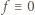 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 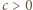 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 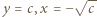 (już wiemy, że
(już wiemy, że 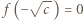 ). Wychodzi
). Wychodzi 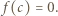 Tak więc
Tak więc 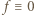 także w przedziale
także w przedziale 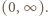
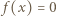 (dla wszystkich
(dla wszystkich 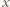 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).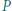 będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień
będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień 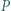 wynosi 1.
wynosi 1.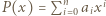 spełnia warunki zadania. Zauważmy, że możemy wybrać
spełnia warunki zadania. Zauważmy, że możemy wybrać 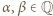 takie, że wielomian
takie, że wielomian 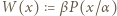 ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech
ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech 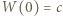 i niech
i niech 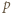 będzie liczbą pierwszą. Jeśli
będzie liczbą pierwszą. Jeśli 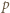 jest dostatecznie duże, to równanie
jest dostatecznie duże, to równanie 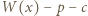 ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie
ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie 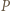 jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko
jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko 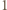 lub
lub 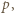 zatem dla dostatecznie dużych
zatem dla dostatecznie dużych 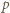 musi to być
musi to być 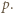 Wynika stąd, że
Wynika stąd, że 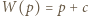 dla dostatecznie dużych liczb pierwszych
dla dostatecznie dużych liczb pierwszych 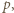 zatem
zatem 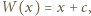 co oznacza, że
co oznacza, że 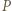 jest stopnia 1.
jest stopnia 1.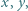 że
że 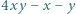 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.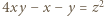 dla pewnych liczb całkowitych
dla pewnych liczb całkowitych 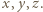 Równość tę możemy przepisać do postaci
Równość tę możemy przepisać do postaci 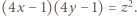 Niech
Niech 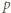 będzie dzielnikiem pierwszym
będzie dzielnikiem pierwszym 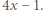 Wówczas
Wówczas 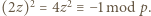 Z Małego Twierdzenia Fermata wiemy, że
Z Małego Twierdzenia Fermata wiemy, że 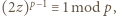 a zatem
a zatem 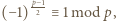 co oznacza że
co oznacza że 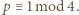 Ponieważ
Ponieważ 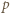 było dowolnym dzielnikiem pierwszym
było dowolnym dzielnikiem pierwszym 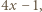 więc
więc 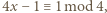 a to jest sprzeczność.
a to jest sprzeczność.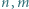 liczba rozwiązań nierówności
liczba rozwiązań nierówności 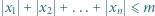 w liczbach całkowitych jest równa liczbie rozwiązań nierówności
w liczbach całkowitych jest równa liczbie rozwiązań nierówności 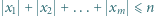 w liczbach całkowitych.
w liczbach całkowitych.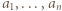 spełniają
spełniają 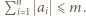 Możemy na dwa sposoby wskazać
Możemy na dwa sposoby wskazać 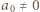 takie, że
takie, że 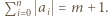 Każdy ciąg
Każdy ciąg 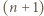 liczb spełniający tę równość (oraz
liczb spełniający tę równość (oraz 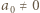 ) możemy podzielić na bloki, czyli fragmenty postaci
) możemy podzielić na bloki, czyli fragmenty postaci 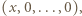 gdzie
gdzie 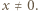 Jeśli długość takiego bloku to
Jeśli długość takiego bloku to 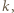 to przyporządkujemy mu blok
to przyporządkujemy mu blok 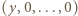 długości
długości 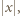 gdzie
gdzie 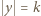 oraz
oraz 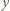 jest tego samego znaku, co
jest tego samego znaku, co 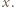 Wykonując tę operację na wszystkich blokach, dostaniemy ciąg
Wykonując tę operację na wszystkich blokach, dostaniemy ciąg 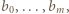 gdzie
gdzie 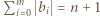 i
i 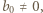 co daje nam ciąg liczb całkowitych
co daje nam ciąg liczb całkowitych 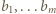 spełniający
spełniający 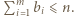 Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.
Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.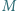 będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru
będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru 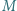 w ciąg
w ciąg 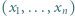 tak, by dla każdej trójki wskaźników
tak, by dla każdej trójki wskaźników 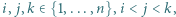 spełniony był warunek:
spełniony był warunek: 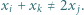
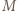 o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru
o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru 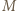 da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru
da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru 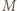 (po wykreśleniu zbędnych elementów).
(po wykreśleniu zbędnych elementów).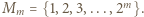 Dla
Dla 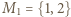 każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego
każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego 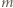 zbiór
zbiór 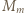 daje się ustawić w ciąg
daje się ustawić w ciąg 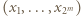 tak, że
tak, że 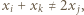 gdy
gdy 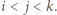 Wówczas ciąg
Wówczas ciąg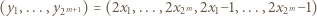
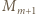 (jednym z możliwych); bo gdy
(jednym z możliwych); bo gdy 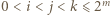 lub
lub 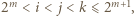 nierówność
nierówność 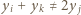 wynika z założenia indukcyjnego; gdy zaś
wynika z założenia indukcyjnego; gdy zaś 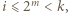 liczba
liczba 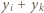 jest nieparzysta, więc
jest nieparzysta, więc 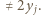 To kończy krok indukcyjny.
To kończy krok indukcyjny.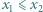 i
i 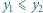 spełniają równości
spełniają równości 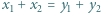 oraz
oraz 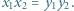 Udowodnić, że
Udowodnić, że 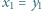 i
i 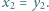
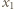 i
i 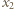 są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby
są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby 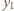 oraz
oraz 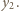
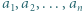 będą ustalonymi liczbami rzeczywistymi. Dla jakiego
będą ustalonymi liczbami rzeczywistymi. Dla jakiego 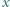 wartość funkcji
wartość funkcji
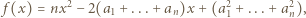
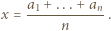
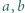 i
i  spełniają nierówność
spełniają nierówność 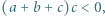 przy czym
przy czym 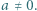 Wykazać, że
Wykazać, że 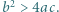
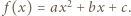 Wówczas mamy
Wówczas mamy 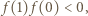 więc funkcja
więc funkcja 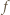 przyjmuje zarówno dodatnie i ujemne wartości, skąd
przyjmuje zarówno dodatnie i ujemne wartości, skąd 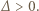
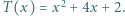
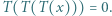
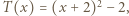
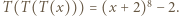
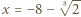
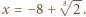
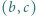
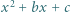
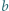
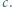
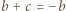
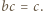
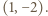


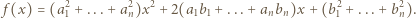
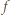 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 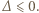 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.