Zagadki liczbowe»Zadanie 8
o zadaniu...
- Zadanie pochodzi z artykułu Zagadki liczbowe
- Publikacja w Delcie: kwiecień 2012
- Publikacja elektroniczna: 01-04-2012
Która liczba jest większa?

Która liczba jest większa?

Która liczba jest większa?
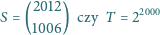
Która liczba jest większa?
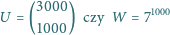
Dany jest wielomian
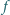 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
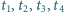 , że
, że

Udowodnić, że nie istnieje liczba całkowita
 , dla której
, dla której
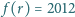 .
.
Zadanie 638 zaproponował pan Paweł Kubit z Krakowa.
Liczby dodatnie
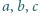 spełniają warunek
spełniają warunek
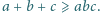 Udowodnić,
że co najwyżej jedna z liczb
Udowodnić,
że co najwyżej jedna z liczb
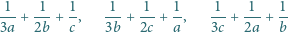
jest mniejsza od 1.
Dane są liczby rzeczywiste
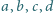 , takie że
, takie że
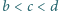 .
Udowodnić nierówność
.
Udowodnić nierówność
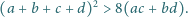
Zadanie zaproponował pan Paweł Najman z Krakowa.
Mamy cztery liczby rzeczywiste; można z nich wybrać parę liczb na
sześć sposobów. W każdej parze dodajemy obie liczby; dostajemy
układ sześciu liczb. Suma tych sześciu liczb jest znana, równa
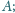 także suma ich kwadratów jest znana, równa
także suma ich kwadratów jest znana, równa
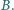 Wyznaczyć
wszystkie wartości, jakie może przyjąć suma sześcianów tych sześciu
liczb.
Wyznaczyć
wszystkie wartości, jakie może przyjąć suma sześcianów tych sześciu
liczb.
Udowodnić, że dla liczb rzeczywistych
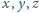 , spełniających
, spełniających
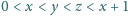 , zachodzi nierówność
, zachodzi nierówność
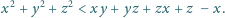
Znaleźć największą liczbę naturalną
 , nie większą od
, nie większą od
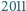 , dla
której liczba
, dla
której liczba
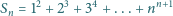
jest podzielna przez 3.
Udowodnić, że dla każdej liczby całkowitej dodatniej
 liczba
liczba
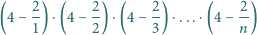
jest całkowita.
Liczby
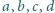 są liczbami rzeczywistymi dodatnimi. Wykaż, że
wśród liczb:
są liczbami rzeczywistymi dodatnimi. Wykaż, że
wśród liczb:

co najmniej dwie są dodatnie.
Udowodnić, że spośród dowolnych pięciu liczb całkowitych (niekoniecznie różnych) można wybrać trzy, których suma jest podzielna przez 3.
Zadanie 628 zaproponował pan Witold Bednarek z Łodzi.
Niech
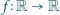 będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
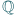 na cały zbiór
na cały zbiór
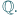 Czy stąd wynika,
że funkcja
Czy stąd wynika,
że funkcja
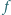 jest przedziałami liniowa (tzn. że
jest przedziałami liniowa (tzn. że
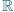 jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
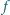 jest
liniowa)?
jest
liniowa)?
Znaleźć wszystkie takie liczby pierwsze
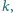 że liczba
że liczba
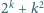 jest
pierwsza.
jest
pierwsza.
Czy można umieścić w polach szachownicy
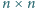 liczby
liczby
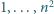 tak, by w każdym wierszu suma liczb była całkowitą
potęgą dwójki?
tak, by w każdym wierszu suma liczb była całkowitą
potęgą dwójki?
Udowodnij, że dla każdych liczb
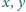 należących do przedziału
należących do przedziału
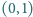 spełniona jest nierówność
spełniona jest nierówność
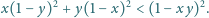
Udowodnić, że dla każdej liczby całkowitej dodatniej
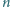 istnieje taka
liczba całkowita dodatnia
istnieje taka
liczba całkowita dodatnia
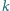 , że
, że
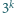 w zapisie dziesiętnym kończy
się cyframi
w zapisie dziesiętnym kończy
się cyframi
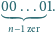
Czy kasjer może wydać 20 zł siedmioma monetami o wartości 1 zł i 5 zł?
Czy istnieją różne liczby pierwsze
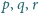 takie, że liczba
takie, że liczba

jest naturalna?
Zadanie zaproponował pan Tomasz Tkocz z Warszawy.
Udowodnić nierówność
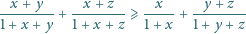
dla liczb