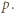Załóżmy, że dodatnie liczby całkowite 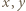 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 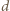 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 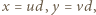 gdzie
gdzie 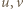 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 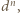 otrzymujemy
otrzymujemy
 |
(1) |
Niech 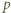 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 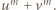 Wobec związku (1)
Wobec związku (1) 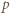 jest też dzielnikiem sumy
jest też dzielnikiem sumy 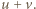 To znaczy, że
To znaczy, że 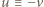 (mod
(mod 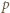 ); a skoro
); a skoro 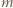 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 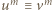 (mod
(mod 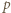 ), i dalej
), i dalej
Liczba  nie dzieli się przez
nie dzieli się przez 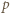 (bo
(bo 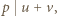 zaś
zaś 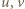 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
Skoro 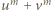 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
 |
(2) |
Zatem liczby 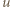 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 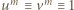 (mod 4), bo
(mod 4), bo 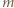 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 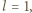 skąd
skąd 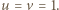 Wracamy do równania (1):
Wracamy do równania (1): 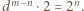 To pokazuje, że
To pokazuje, że 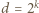 (dla pewnego
(dla pewnego 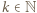 ); przy tym
); przy tym 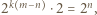 czyli
czyli 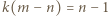 : liczba
: liczba 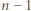 dzieli się przez
dzieli się przez 
Na odwrót, załóżmy, że 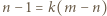 dla pewnego
dla pewnego 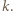 Wówczas para
Wówczas para 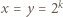 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania:
Uzyskaliśmy żądaną równoważność.
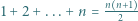 i
i 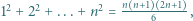 wyprowadzić wzór na
wyprowadzić wzór na 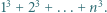
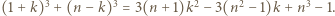
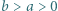 zachodzi nierówność
zachodzi nierówność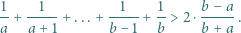
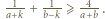
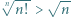 dla naturalnych
dla naturalnych 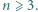
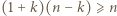 dla
dla 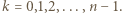 Ponadto dla
Ponadto dla 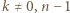 nierówność jest ostra.
nierówność jest ostra. zachodzą następujące równości:
zachodzą następujące równości: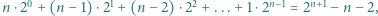
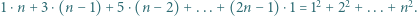
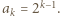
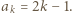 Przyda się też równość
Przyda się też równość 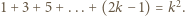
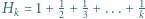 dla całkowitych dodatnich
dla całkowitych dodatnich 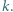 Udowodnić, że
Udowodnić, że 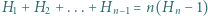 dla naturalnych
dla naturalnych 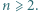
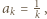 gdzie
gdzie 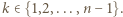
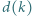 oznacza liczbę dzielników liczby naturalnej
oznacza liczbę dzielników liczby naturalnej 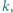 zaś
zaś 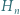 - jak w poprzednim zadaniu. Dowieść, że
- jak w poprzednim zadaniu. Dowieść, że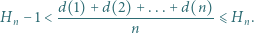
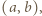 dla których
dla których 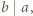 gdzie
gdzie 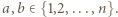 Po sporządzeniu tabeli w kolumnach mamy kolejno
Po sporządzeniu tabeli w kolumnach mamy kolejno 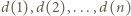 par, a w wierszach
par, a w wierszach 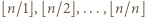 par. Trzeba jeszcze zastosować nierówność
par. Trzeba jeszcze zastosować nierówność 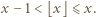
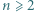 zachodzi równość
zachodzi równość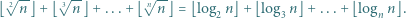
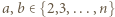 zaznaczamy takie pola
zaznaczamy takie pola 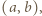 dla których
dla których 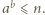 Wówczas w
Wówczas w 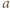 -tej kolumnie mamy
-tej kolumnie mamy 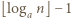 zaznaczonych pól, zaś w
zaznaczonych pól, zaś w 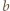 -tym wierszu jest ich
-tym wierszu jest ich 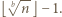
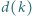 będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą
będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą 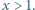 Dowieść, że dla wszystkich naturalnych
Dowieść, że dla wszystkich naturalnych 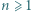 zachodzi nierówność
zachodzi nierówność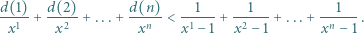
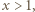 mamy
mamy 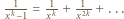 Dla
Dla 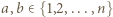 w polu
w polu 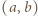 tabeli umieszczamy liczbę
tabeli umieszczamy liczbę 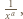 jeśli
jeśli 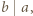 w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.
w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.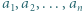 spełniają równości
spełniają równości 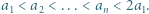 Udowodnić, że jeśli
Udowodnić, że jeśli 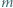 jest liczbą różnych dzielników pierwszych iloczynu
jest liczbą różnych dzielników pierwszych iloczynu 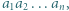 to
to 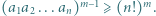
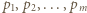 będą różnymi dzielnikami pierwszymi iloczynu
będą różnymi dzielnikami pierwszymi iloczynu 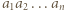 oraz niech
oraz niech 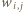 oznacza wykładnik liczby
oznacza wykładnik liczby 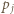 w rozkładzie
w rozkładzie 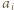 na czynniki pierwsze dla
na czynniki pierwsze dla 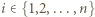 i
i 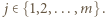 W pole tabeli o współrzędnych
W pole tabeli o współrzędnych 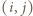 wpisujemy
wpisujemy 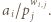 Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej
Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej 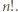 Ponadto iloczyny liczb w kolejnych kolumnach są równe
Ponadto iloczyny liczb w kolejnych kolumnach są równe 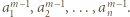
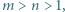 przy czym
przy czym 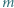 jest liczbą parzystą. Udowodnić, że równanie
jest liczbą parzystą. Udowodnić, że równanie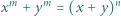
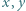 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 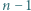 dzieli się przez
dzieli się przez 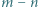 .
.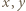 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 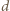 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 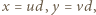 gdzie
gdzie 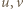 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 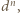 otrzymujemy
otrzymujemy
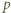 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 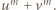 Wobec związku (1)
Wobec związku (1) 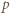 jest też dzielnikiem sumy
jest też dzielnikiem sumy 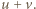 To znaczy, że
To znaczy, że 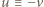 (mod
(mod 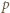 ); a skoro
); a skoro 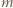 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 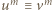 (mod
(mod 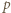 ), i dalej
), i dalej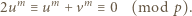
 nie dzieli się przez
nie dzieli się przez 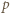 (bo
(bo 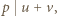 zaś
zaś 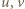 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
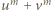 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
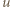 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 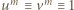 (mod 4), bo
(mod 4), bo 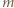 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 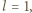 skąd
skąd 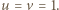 Wracamy do równania (1):
Wracamy do równania (1): 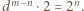 To pokazuje, że
To pokazuje, że 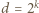 (dla pewnego
(dla pewnego 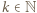 ); przy tym
); przy tym 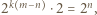 czyli
czyli 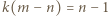 : liczba
: liczba 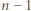 dzieli się przez
dzieli się przez 
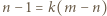 dla pewnego
dla pewnego 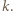 Wówczas para
Wówczas para 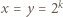 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania: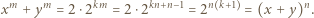
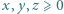 przyjmijmy:
przyjmijmy: 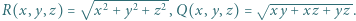 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia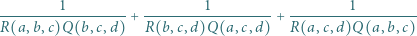
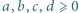 spełniających warunek
spełniających warunek 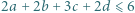 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 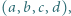 dla których to minimum jest osiągane.
dla których to minimum jest osiągane.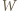 (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):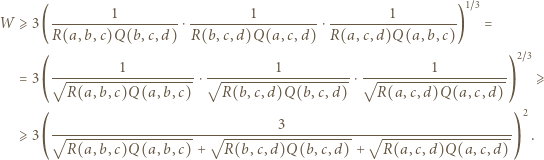
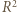 i
i 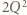 ), dostajemy oszacowanie
), dostajemy oszacowanie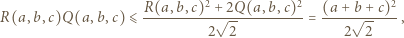
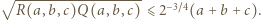 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 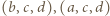 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności: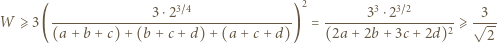
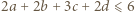 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 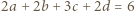 oraz
oraz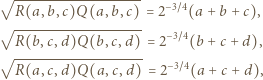
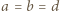 oraz
oraz 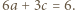 Ponadto - oznaczając krótko
Ponadto - oznaczając krótko 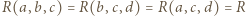 (i podobnie
(i podobnie 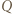 ) - musimy mieć równość
) - musimy mieć równość 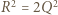 (do takiej pary też była stosowana nierówność między średnimi) - czyli
(do takiej pary też była stosowana nierówność między średnimi) - czyli 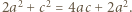 Wraz z równością
Wraz z równością 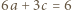 daje to alternatywę:
daje to alternatywę: 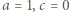 lub
lub 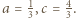 Dla czwórek
Dla czwórek 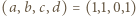 oraz
oraz 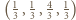 wyznaczone oszacowanie
wyznaczone oszacowanie 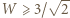 przechodzi w równość. Zatem szukane minimum wynosi
przechodzi w równość. Zatem szukane minimum wynosi 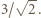
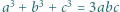 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 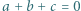 lub
lub 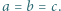
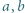 spełniają równość
spełniają równość 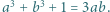 Wyznaczyć wszystkie możliwe wartości wyrażenia
Wyznaczyć wszystkie możliwe wartości wyrażenia 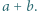
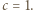 Są tu dwa przypadki do rozważania.
Są tu dwa przypadki do rozważania.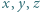 są rzeczywiste. Udowodnić, że jeśli
są rzeczywiste. Udowodnić, że jeśli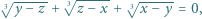
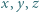 są równe.
są równe.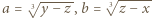 i
i 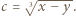
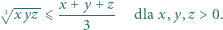
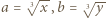 i
i 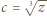 w tożsamości.
w tożsamości.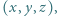 które spełniają równości
które spełniają równości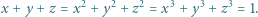
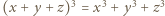 i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb
i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb 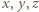 występuje co najmniej jedna para liczb przeciwnych.
występuje co najmniej jedna para liczb przeciwnych.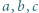 spełniają równość
spełniają równość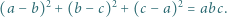
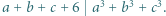
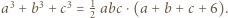 Wystarczy teraz wykazać, że co najmniej jedna z liczb
Wystarczy teraz wykazać, że co najmniej jedna z liczb 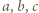 jest parzysta. To wynika z równości danej w zadaniu.
jest parzysta. To wynika z równości danej w zadaniu.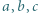 są całkowite. Wykazać, że jeśli liczba
są całkowite. Wykazać, że jeśli liczba 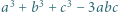 dzieli się przez 3, to dzieli się ona również przez 9.
dzieli się przez 3, to dzieli się ona również przez 9.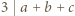 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 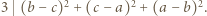 To ma miejsce dokładnie wtedy, gdy liczby
To ma miejsce dokładnie wtedy, gdy liczby 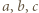 dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.
dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.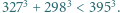 Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.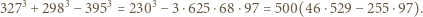
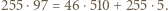
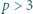 oraz takie liczby całkowite dodatnie
oraz takie liczby całkowite dodatnie 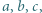 że
że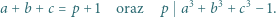
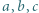 jest równa 1.
jest równa 1.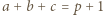 i
i 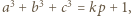 gdzie
gdzie 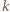 jest jakąś liczbą całkowitą. Wywnioskować stąd, że
jest jakąś liczbą całkowitą. Wywnioskować stąd, że 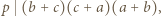 więc któryś z czynników dzieli się przez
więc któryś z czynników dzieli się przez 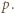 Te czynniki są dodatnie i nie przekraczają
Te czynniki są dodatnie i nie przekraczają 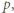 więc któryś z nich jest równy
więc któryś z nich jest równy