Zadanie ZM-1310
o zadaniu...
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31-03-2011
Znaleźć wszystkie liczby naturalne, których nie da się zapisać jako sumy co najmniej dwóch kolejnych liczb całkowitych dodatnich.
Znaleźć wszystkie liczby naturalne, których nie da się zapisać jako sumy co najmniej dwóch kolejnych liczb całkowitych dodatnich.
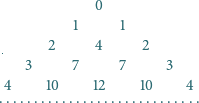
Diagram przedstawia początkowe wiersze nieskończonej tabeli trójkątnej.
Skrajnymi elementami kolejnych wierszy są kolejne liczby naturalne. Ponadto
obowiązuje reguła: jeśli liczby
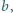
 są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
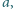 zaś pod nimi liczba
zaś pod nimi liczba
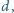 to
to
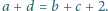 Udowodnić, że dla każdej liczby
całkowitej
Udowodnić, że dla każdej liczby
całkowitej
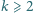 istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
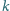 razy.
razy.
Udowodnić, że spośród dowolnych
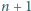 liczb ze zbioru
liczb ze zbioru
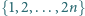 można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
Znaleźć wszystkie funkcje
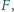 określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
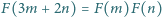 dla każdej pary liczb
całkowitych
dla każdej pary liczb
całkowitych
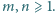
Dane są liczby całkowite dodatnie
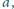
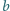 o następującej własności:
o następującej własności:
dla każdej liczby całkowitej dodatniej
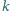 liczby
liczby
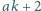 oraz
oraz
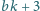 nie są względnie pierwsze. Udowodnić, że
nie są względnie pierwsze. Udowodnić, że
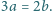
Znaleźć wszystkie liczby rzeczywiste
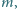 dla których nierówność
dla których nierówność
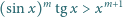
jest spełniona dla
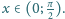
Zadanie zaproponował pan Paweł Kubit z Krakowa.
Udowodnić nierówność dla liczb dodatnich
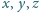 :
:
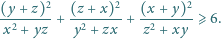
Udowodnić, że dla dowolnych liczb całkowitych dodatnich
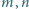 i dla
dowolnych liczb rzeczywistych nieujemnych
i dla
dowolnych liczb rzeczywistych nieujemnych
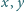 spełniających warunek
spełniających warunek
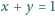 zachodzi nierówność
zachodzi nierówność
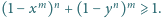
Udowodnij, że dla każdego
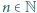 prawdziwe są poniższe nierówności
pomiędzy średnią arytmetyczną i geometryczną
prawdziwe są poniższe nierówności
pomiędzy średnią arytmetyczną i geometryczną
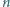 dodatnich liczb
rzeczywistych.
dodatnich liczb
rzeczywistych.

Rozwiązać równanie
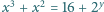 w liczbach całkowitych
w liczbach całkowitych
Zadanie 614 zaproponował pan Paweł Najman z Jaworzna.
Wyznaczyć wszystkie liczby wymierne
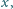 niecałkowite, dla których
wartość wyrażenia
niecałkowite, dla których
wartość wyrażenia
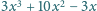 jest liczbą całkowitą.
jest liczbą całkowitą.
Udowodnij, że nie istnieją liczby nieparzyste
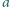 i
i
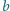 spełniające
równanie
spełniające
równanie
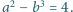
Czy istnieją różne liczby pierwsze
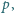
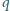 i
i
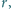 dla których
liczba
dla których
liczba
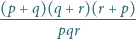
jest liczbą całkowitą? Odpowiedź uzasadnij.
Niech
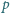 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci
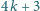 . Dowieść, że
zbioru złożonego z
. Dowieść, że
zbioru złożonego z
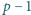 kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
Wyznaczyć wszystkie liczby całkowite dodatnie
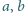 , dla których liczba
, dla których liczba
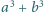 jest czwartą potęgą liczby pierwszej.
jest czwartą potęgą liczby pierwszej.
Dowieść, że dla każdej parzystej liczby naturalnej
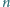 oraz dla każdej
liczby rzeczywistej
oraz dla każdej
liczby rzeczywistej
 zachodzi nierówność
zachodzi nierówność
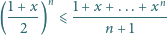
Niech
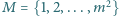 , gdzie
, gdzie
 jest ustaloną liczbą naturalną.
jest ustaloną liczbą naturalną.
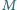 podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
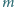 ?
?
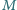 podzbiorów niezawierających pary liczb,
których różnica jest
równa
podzbiorów niezawierających pary liczb,
których różnica jest
równa
 ?
?Zadanie zaproponował pan Paweł Kubit z Krakowa.
Dane są takie liczby wymierne
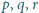 , dla których
, dla których
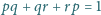 .
Wykazać, że liczba
.
Wykazać, że liczba
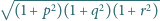
jest wymierna.
Wyznaczyć najmniejszą liczbą naturalną, której nie da się przedstawić w postaci

gdzie
 ,
,
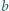 ,
,
 ,
,
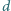 są liczbami całkowitymi dodatnimi.
są liczbami całkowitymi dodatnimi.
Rozstrzygnąć, czy istnieje 19-cyfrowa liczba naturalna N podzielna przez 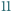 o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez
o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez