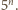Zadanie ZM-1545
o zadaniu...
- Publikacja w Delcie: październik 2017
- Publikacja elektroniczna: 29 września 2017
Niech 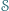 będzie takim podzbiorem zbioru
będzie takim podzbiorem zbioru 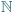 dodatnich liczb całkowitych, że dla każdej pary
dodatnich liczb całkowitych, że dla każdej pary 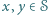 również
również 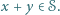 Przypuśćmy, że zbiór
Przypuśćmy, że zbiór 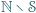 jest skończony i
jest skończony i 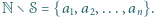 Udowodnić, że
Udowodnić, że

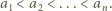
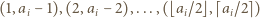
 Rzeczywiście, gdyby w pewnej parze obie liczby należały do
Rzeczywiście, gdyby w pewnej parze obie liczby należały do  to ich suma także, co przeczy definicji
to ich suma także, co przeczy definicji  Z drugiej strony liczb spoza
Z drugiej strony liczb spoza 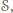 które są mniejsze od
które są mniejsze od 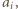 jest dokładnie
jest dokładnie  Stąd
Stąd 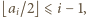 a zatem
a zatem 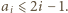 Sumując te nierówności dla
Sumując te nierówności dla 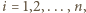 uzyskujemy
uzyskujemy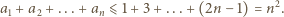
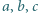 są takie, że
są takie, że 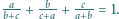 Sprawdzić, że wartość wyrażenia
Sprawdzić, że wartość wyrażenia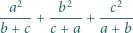
 uzyskujemy
uzyskujemy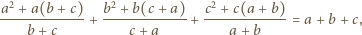
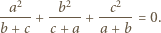
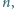 dla których każda z liczb
dla których każda z liczb 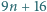 oraz
oraz 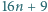 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.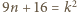 oraz
oraz 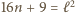 dla pewnych dodatnich liczb całkowitych
dla pewnych dodatnich liczb całkowitych 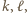 to
to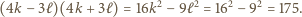
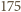 ma trzy przedstawienia w postaci iloczynu dwóch dodatnich liczb całkowitych:
ma trzy przedstawienia w postaci iloczynu dwóch dodatnich liczb całkowitych: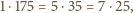
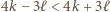 prowadzi do par
prowadzi do par 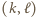 :
: 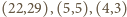 i w konsekwencji do
i w konsekwencji do 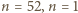 lub
lub 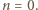 Bezpośrednio sprawdzamy, że każda z tych liczb ma żądaną własność.
Bezpośrednio sprawdzamy, że każda z tych liczb ma żądaną własność.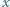 oraz dla każdej dodatniej liczby całkowitej
oraz dla każdej dodatniej liczby całkowitej 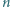 istnieje co najmniej
istnieje co najmniej 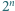 różnych wyborów znaków
różnych wyborów znaków 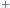 i
i  w wyrażeniu
w wyrażeniu 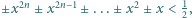 dla których ta nierówność jest spełniona.
dla których ta nierówność jest spełniona.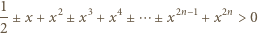
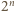 możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci
możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci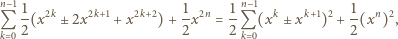
 oraz
oraz 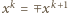 (dla
(dla 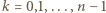 i pewnych wyborów znaków
i pewnych wyborów znaków 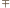 ) nie mogą wszystkie zachodzić jednocześnie.
) nie mogą wszystkie zachodzić jednocześnie.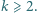 Czy istnieje rosnący ciąg liczb naturalnych
Czy istnieje rosnący ciąg liczb naturalnych 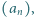 którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest
którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest 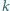 -tą potęgą liczby naturalnej, a przy tym ciąg
-tą potęgą liczby naturalnej, a przy tym ciąg 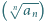 jest ograniczony?
jest ograniczony?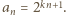
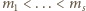 :
: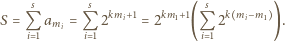
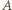 zachodziła równość
zachodziła równość 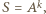 wówczas pisząc
wówczas pisząc 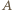 w postaci
w postaci 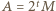 (
( 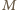 nieparzyste) i przyrównując potęgi dwójki w
nieparzyste) i przyrównując potęgi dwójki w 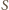 i w
i w 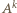 uzyskalibyśmy równość
uzyskalibyśmy równość 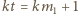 ; oczywista sprzeczność.
; oczywista sprzeczność.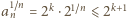 jest ograniczony.
jest ograniczony.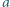 i
i 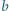 jest równy
jest równy 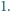 Dowieść, że największy wspólny dzielnik liczb
Dowieść, że największy wspólny dzielnik liczb 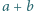 i
i 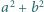 nie przekracza
nie przekracza 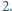
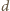 największy wspólny dzielnik liczb
największy wspólny dzielnik liczb 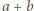 i
i 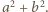 Ponieważ liczby
Ponieważ liczby 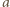 i
i 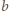 są względnie pierwsze, a ich suma jest podzielna przez
są względnie pierwsze, a ich suma jest podzielna przez 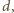 więc liczba
więc liczba 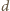 jest względnie pierwsza z liczbami
jest względnie pierwsza z liczbami 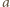 i
i 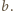 Ponadto liczba
Ponadto liczba 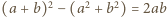 jest podzielna przez
jest podzielna przez 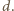 Stąd wynika, że
Stąd wynika, że 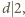 czyli
czyli 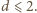
 spełniają warunek
spełniają warunek 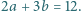 Wykazać, że dla każdej liczby naturalnej
Wykazać, że dla każdej liczby naturalnej 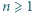 zachodzi nierówność
zachodzi nierówność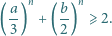
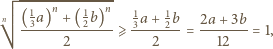
 dla pewnych liczb naturalnych
dla pewnych liczb naturalnych 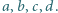
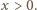
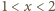 ; tak więc
; tak więc 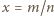
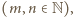
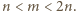 W tym przypadku wystarczy przyjąć
W tym przypadku wystarczy przyjąć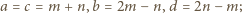
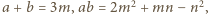
![a3 + b3 = (a +b)[(a + b)2− 3ab] = 3m(3m2](/math/temat/matematyka/algebra/zadania/2017/08/22/zm-k44-495/7x-65a3a08157267fadfd427493aa9c892345a613f2-dm-66,57,43-FF,FF,FF.gif)
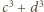 i otrzymujemy
i otrzymujemy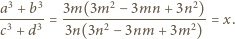
 jest dowolną liczbą wymierną dodatnią, znajdujemy liczbę wymierną
jest dowolną liczbą wymierną dodatnią, znajdujemy liczbę wymierną 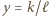 taką, że
taką, że 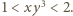 W myśl konkluzji poprzedniego przypadku liczba
W myśl konkluzji poprzedniego przypadku liczba 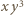 daje się zapisać jako ułamek
daje się zapisać jako ułamek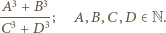
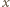 :
: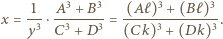
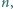 dla której
dla której 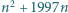 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.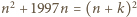 dla pewnego naturalnego
dla pewnego naturalnego 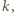 to
to 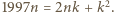 Stąd
Stąd 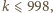 a wtedy
a wtedy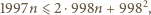
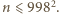 Z drugiej strony
Z drugiej strony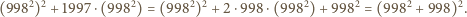
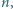 dla której istnieją czteroelementowe zbiory
dla której istnieją czteroelementowe zbiory 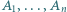 o następującej własności: każdy zbiór
o następującej własności: każdy zbiór 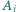 ma z każdym innym zbiorem
ma z każdym innym zbiorem 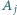 dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów
dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów 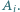
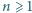 oraz pewien zbiór
oraz pewien zbiór 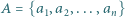 dodatnich liczb całkowitych. Na okręgu wyróżniono
dodatnich liczb całkowitych. Na okręgu wyróżniono 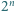 punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru
punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru 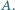 Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej. Dla każdej liczby
Dla każdej liczby 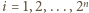 zdefiniujmy
zdefiniujmy 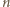 -wyrazowy ciąg binarny
-wyrazowy ciąg binarny 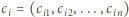 następująco:
następująco: 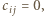 jeżeli pośród liczb
jeżeli pośród liczb 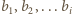 wartość
wartość 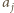 występuje parzystą liczbę razy oraz
występuje parzystą liczbę razy oraz 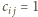 w przeciwnym przypadku.
w przeciwnym przypadku.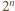 binarnych ciągów długości
binarnych ciągów długości 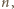 więc albo ciągi
więc albo ciągi 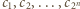 są parami różne i
są parami różne i 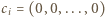 dla pewnego
dla pewnego 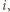 albo
albo 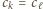 dla pewnych
dla pewnych 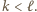 W pierwszym przypadku iloczyn liczb
W pierwszym przypadku iloczyn liczb 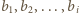 jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb
jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb 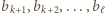 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej. będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby  w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.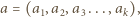
 nazwiemy kompozycją liczby
nazwiemy kompozycją liczby 
 -elementowe kompozycje liczby
-elementowe kompozycje liczby 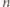 pozostają we wzajemnie jednoznacznej odpowiedniości z
pozostają we wzajemnie jednoznacznej odpowiedniości z 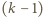 -elementowymi podzbiorami zbioru
-elementowymi podzbiorami zbioru 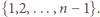 Każdej takiej kompozycji
Każdej takiej kompozycji 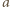 możemy przypisać zbiór
możemy przypisać zbiór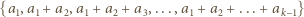
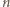 jest równa liczbie podzbiorów zbioru
jest równa liczbie podzbiorów zbioru 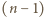 -elementowego, czyli
-elementowego, czyli 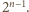
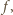 która przyporządkowuje każdej kompozycji
która przyporządkowuje każdej kompozycji  liczby
liczby 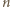 pewną kompozycję następująco: jeżeli
pewną kompozycję następująco: jeżeli 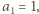 to
to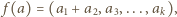
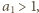 to
to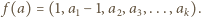
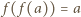 dla każdej kompozycji
dla każdej kompozycji 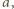 więc
więc 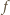 zadaje podział zbioru wszystkich kompozycji liczby
zadaje podział zbioru wszystkich kompozycji liczby 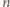 na pary. Wprost z definicji
na pary. Wprost z definicji 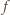 wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli
wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli 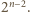
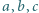 większe od
większe od 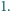 Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań
Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań 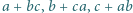 oraz
oraz 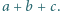 Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?
Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?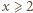 oraz
oraz 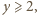 to
to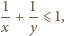
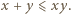 To oznacza, że
To oznacza, że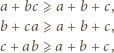
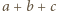 ; oznaczmy tę liczbę przez
; oznaczmy tę liczbę przez 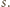 Pozostałe liczby oznaczmy przez
Pozostałe liczby oznaczmy przez  i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że
i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że 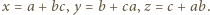 Wówczas
Wówczas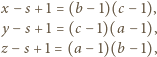
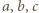 są większe od
są większe od 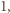 to
to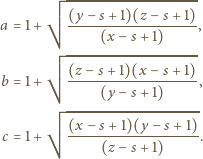
 Niech
Niech 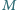 będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb
będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb 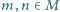 zachodzi nierówność
zachodzi nierówność 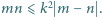 Wykazać, że zbiorze
Wykazać, że zbiorze 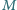 jest nie więcej niż
jest nie więcej niż 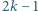 liczb. Czy dla każdej liczby
liczb. Czy dla każdej liczby 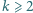 istnieje
istnieje 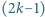 -elementowy zbiór
-elementowy zbiór 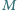 o podanej własności?
o podanej własności? Niech
Niech 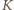 będzie zbiorem odwrotności wszystkich liczb za zbioru
będzie zbiorem odwrotności wszystkich liczb za zbioru 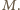 Dowolne dwa elementy zbioru
Dowolne dwa elementy zbioru 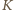 są więc oddalone o co najmniej
są więc oddalone o co najmniej 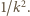 Zatem w każdym spośród
Zatem w każdym spośród 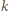 przedziałów
przedziałów![(0, 1-], (-1,-2-], ( 2-,-3] ,...,( k-−1, k-] k2 k2 k2 k2 k2 k2 k2](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/7x-d28462c3f0c14c690f4776454216c605e7515ddb-dm-66,57,43-FF,FF,FF.gif)
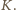 Pozostałe liczby dodatnie tworzą przedział
Pozostałe liczby dodatnie tworzą przedział 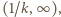 w którym są jedynie odwrotności liczb naturalnych
w którym są jedynie odwrotności liczb naturalnych 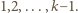 To pokazuje, że zbiór
To pokazuje, że zbiór 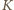 (więc i zbiór
(więc i zbiór 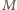 ) może liczyć co najwyżej
) może liczyć co najwyżej 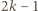 elementów.
elementów.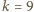 nie istnieje
nie istnieje 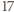 -elementowy zbiór
-elementowy zbiór 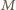 o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów
o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów ![|(0, 181] ,( 181,821],(821, 381]](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/4x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) może być tylko jeden element zbioru
może być tylko jeden element zbioru 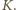 Dalej, odwrotności liczb naturalnych, leżące w przedziale
Dalej, odwrotności liczb naturalnych, leżące w przedziale ![(-1, 1] , 27 9](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/6x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) rozbijamy na pięć podzbiorów:
rozbijamy na pięć podzbiorów: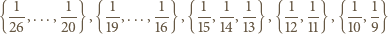
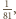 więc zawiera co najwyżej jeden element zbioru
więc zawiera co najwyżej jeden element zbioru 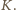 No i zostają jeszcze ułamki
No i zostają jeszcze ułamki 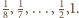 Liczność zbioru
Liczność zbioru 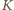 (więc i
(więc i 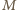 ) nie przekracza
) nie przekracza 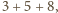 czyli 16.
czyli 16.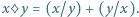 Niech
Niech 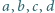 będą liczbami, spełniającymi równanie
będą liczbami, spełniającymi równanie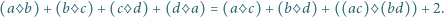
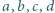 mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?
mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?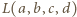 oznacza lewą stronę podanego równania, pomnożoną przez
oznacza lewą stronę podanego równania, pomnożoną przez 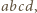 i niech
i niech 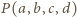 oznacza prawą stronę tego równania, pomnożoną przez
oznacza prawą stronę tego równania, pomnożoną przez 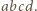 Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np.
Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np. 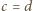 :
: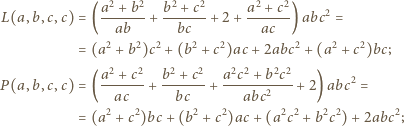
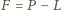 dzieli się przez dwumian
dzieli się przez dwumian 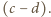 Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany
Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany 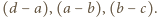 Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby
Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby 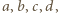 stwierdzamy, że ta stała to 1. Tak więc
stwierdzamy, że ta stała to 1. Tak więc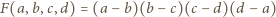
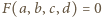 nie jest spełnione dla żadnej czwórki różnych liczb
nie jest spełnione dla żadnej czwórki różnych liczb 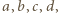 jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem). będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci 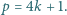 Dowieść, że istnieje liczba całkowita dodatnia
Dowieść, że istnieje liczba całkowita dodatnia 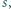 mniejsza od
mniejsza od 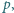 dla której różnica
dla której różnica 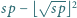 jest kwadratem liczby całkowitej dodatniej.
jest kwadratem liczby całkowitej dodatniej.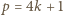 jest sumą dwóch kwadratów (jedno z dobrze znanych twierdzeń Fermata):
jest sumą dwóch kwadratów (jedno z dobrze znanych twierdzeń Fermata): 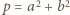 ; liczby całkowite
; liczby całkowite 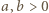 muszą być względnie pierwsze. Istnieją wobec tego liczby całkowite
muszą być względnie pierwsze. Istnieją wobec tego liczby całkowite 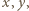 dla których
dla których 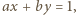 przy czym
przy czym 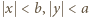 (łatwe uzasadnienie przez algorytm Euklidesa).
(łatwe uzasadnienie przez algorytm Euklidesa).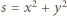 ma własności, o które chodzi w zadaniu. Mamy bowiem oszacowanie
ma własności, o które chodzi w zadaniu. Mamy bowiem oszacowanie 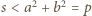 oraz równość
oraz równość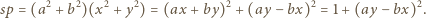
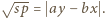 W konsekwencji
W konsekwencji 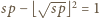 ; jest to niewątpliwie kwadrat liczby całkowitej dodatniej.
; jest to niewątpliwie kwadrat liczby całkowitej dodatniej.
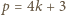 zachodzi równość
zachodzi równość 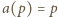 ; natomiast dla liczb pierwszych
; natomiast dla liczb pierwszych 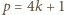 zachodzi nierówność
zachodzi nierówność 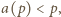 i to była treść naszego zadania; autorem podanego dowodu jest Robert Israel. (Dla liczb złożonych ciąg zachowuje się dość kapryśnie).
i to była treść naszego zadania; autorem podanego dowodu jest Robert Israel. (Dla liczb złożonych ciąg zachowuje się dość kapryśnie).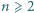 liczba
liczba 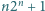 jest pierwsza, to liczby
jest pierwsza, to liczby 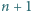 oraz
oraz 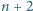 są złożone.
są złożone.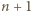 jest nieparzystą liczbą pierwszą. Wówczas z małego twierdzenia Fermata wynika, że liczba
jest nieparzystą liczbą pierwszą. Wówczas z małego twierdzenia Fermata wynika, że liczba 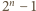 jest podzielna przez
jest podzielna przez 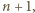 a zatem również
a zatem również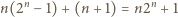
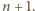 To przeczy pierwszości liczby
To przeczy pierwszości liczby 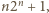 gdyż
gdyż 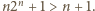
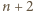 jest nieparzystą liczbą pierwszą, to z małego twierdzenia Fermata wynika, że liczba
jest nieparzystą liczbą pierwszą, to z małego twierdzenia Fermata wynika, że liczba 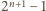 jest podzielna przez
jest podzielna przez 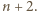 Wobec tego również liczba
Wobec tego również liczba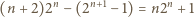
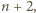 ale
ale 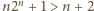 na mocy nierówności
na mocy nierówności 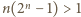 prawdziwej dla
prawdziwej dla 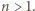
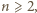 dla której
dla której 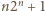 jest liczbą pierwszą, jest
jest liczbą pierwszą, jest 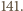 Liczby postaci
Liczby postaci 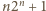 nazywane są liczbami Cullena.
nazywane są liczbami Cullena.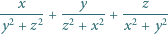
 mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 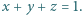
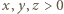 o sumie równej 1. Funkcja
o sumie równej 1. Funkcja 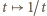 jest wypukła w przedziale
jest wypukła w przedziale 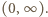 Stosujemy do niej nierówność Jensena dla trójki punktów
Stosujemy do niej nierówność Jensena dla trójki punktów 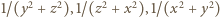 z wagami
z wagami 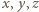 :
: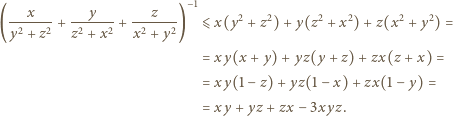
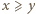 oraz
oraz 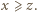 Wówczas
Wówczas 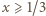 oraz
oraz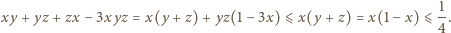
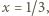 zaś druga - tylko dla
zaś druga - tylko dla 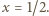 Stąd wniosek, że
Stąd wniosek, że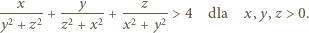
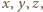 wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla
wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla 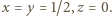 Przy założeniu, że
Przy założeniu, że 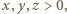 wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla
wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla 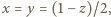 gdy
gdy 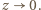 Jest więc jej kresem dolnym.
Jest więc jej kresem dolnym. o następujących własnościach:
o następujących własnościach: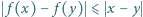 dla
dla 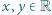 ;
;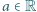 ciąg
ciąg 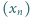 określony wzorami
określony wzorami 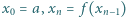 (dla
(dla 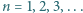 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.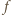 będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja
będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja 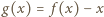 nie jest stała. Istnieją więc liczby
nie jest stała. Istnieją więc liczby 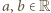 dla których
dla których 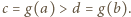 W drugim z warunków, podanych w zadaniu, przyjmujemy
W drugim z warunków, podanych w zadaniu, przyjmujemy 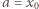 i tworzymy ciąg arytmetyczny
i tworzymy ciąg arytmetyczny 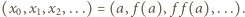 Skoro
Skoro 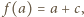 zatem
zatem 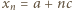 (dla wszystkich
(dla wszystkich  ). Jednocześnie
). Jednocześnie 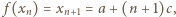 czyli
czyli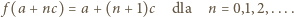
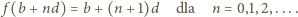
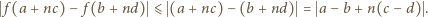
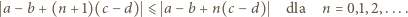
 wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo
wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo 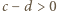 ). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci
). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci 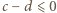 ; sprzeczność.
; sprzeczność.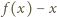 musi być stała. Jasne, że każda funkcja postaci
musi być stała. Jasne, że każda funkcja postaci 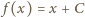 spełnia wymagane warunki.
spełnia wymagane warunki.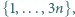 które nie zawierają dwóch liczb różniących się o
które nie zawierają dwóch liczb różniących się o 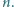
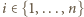 jest dokładnie pięć możliwości opisujących, które z liczb
jest dokładnie pięć możliwości opisujących, które z liczb 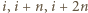 należą do podzbioru spełniającego warunek zadania. Mianowicie:
należą do podzbioru spełniającego warunek zadania. Mianowicie: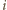 należy;
należy;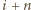 należy;
należy;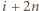 należy;
należy;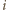 oraz
oraz 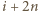 należą (natomiast
należą (natomiast 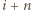 nie należy).
nie należy).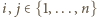 możliwości te są niezależne, to liczba szukanych pozdbiorów wynosi
możliwości te są niezależne, to liczba szukanych pozdbiorów wynosi