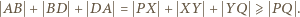a) Pewien wierzchołek otrzymuje nazwę 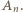 Idąc od
Idąc od 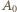 do
do 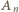 wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki
wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki 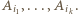 Przechodzimy przez
Przechodzimy przez 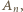 dalej mijamy wierzchołki
dalej mijamy wierzchołki 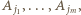 i wracamy do
i wracamy do 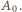 Numery
Numery 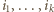 oraz
oraz 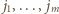 tworzą permutację zbioru
tworzą permutację zbioru 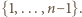 Liczby, przyporządkowane wszystkim bokom, sumują się do wartości
Liczby, przyporządkowane wszystkim bokom, sumują się do wartości
Równość w tym szacowaniu jest osiągalna; ma ona miejsce wtedy i tylko wtedy, gdy 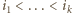 oraz
oraz 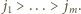 Zatem
Zatem 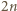 to szukane minimum.
to szukane minimum.
b) Zbiór 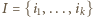 może być dowolnym podzbiorem zbioru
może być dowolnym podzbiorem zbioru 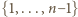 (również pustym, wtedy pierwszy składnik rozpisanej sumy
(również pustym, wtedy pierwszy składnik rozpisanej sumy 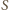 ma postać
ma postać 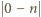 ). Zauważmy teraz, że już sam wybór zbioru
). Zauważmy teraz, że już sam wybór zbioru 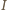 determinuje ponumerowanie, realizujące równość
determinuje ponumerowanie, realizujące równość 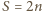 ; liczby ze zbioru
; liczby ze zbioru 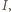 uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od
uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od 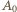 w wybranym kierunku), następny wierzchołek trzeba nazwać
w wybranym kierunku), następny wierzchołek trzeba nazwać 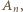 a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.
a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.
Konkluzja: jest tyle możliwości optymalnego ponumerowania 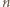 wierzchołków, ile podzbiorów ma zbiór
wierzchołków, ile podzbiorów ma zbiór 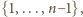 to znaczy
to znaczy 
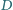 i
i 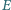 leżą odpowiednio na bokach
leżą odpowiednio na bokach 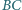 i
i 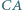 trójkąta
trójkąta 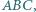 przy czym
przy czym 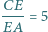 oraz
oraz 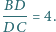 Odcinki
Odcinki 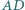 i
i 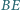 przecinają się w punkcie
przecinają się w punkcie 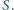 W jakim stosunku punkt
W jakim stosunku punkt 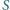 dzieli odcinek
dzieli odcinek 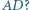
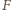 będzie takim punktem na odcinku
będzie takim punktem na odcinku 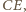 że proste
że proste 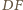 i
i 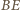 są równoległe. Wówczas z twierdzenia Talesa otrzymujemy
są równoległe. Wówczas z twierdzenia Talesa otrzymujemy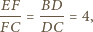
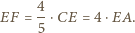
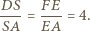
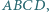 w którym boki
w którym boki 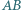 i
i 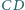 nie są równoległe. Rozważamy okrąg, przechodzący przez punkty
nie są równoległe. Rozważamy okrąg, przechodzący przez punkty 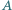 i
i 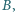 styczny do prostej
styczny do prostej 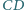 w punkcie
w punkcie 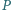 oraz okrąg, przechodzący przez punkty
oraz okrąg, przechodzący przez punkty 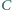 i
i 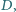 styczny do prostej
styczny do prostej 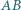 w punkcie
w punkcie 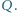 Zakładamy, że punkty
Zakładamy, że punkty 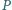 i
i 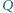 leżą na odcinkach
leżą na odcinkach 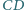 i
i 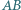 oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka
oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka 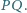 Udowodnić, że proste
Udowodnić, że proste 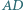 i
i 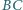 są równoległe.
są równoległe.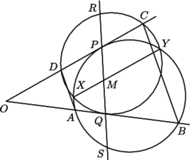
 przecięcia prostych
przecięcia prostych 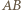 i
i 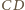 leży na półprostych
leży na półprostych 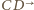 i
i 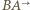 oraz że prosta
oraz że prosta 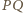 przecina okręgi
przecina okręgi 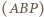 i
i 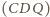 odpowiednio w punktach
odpowiednio w punktach 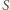 i
i 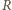 (różnych od
(różnych od 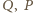 ). Wspólna cięciwa tych okręgów - nazwijmy ją
). Wspólna cięciwa tych okręgów - nazwijmy ją 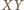 - przechodzi przez środek
- przechodzi przez środek 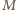 odcinka
odcinka 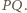 Z równości
Z równości 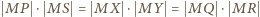 oraz
oraz 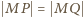 wnosimy, że
wnosimy, że 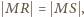 a stąd
a stąd 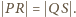
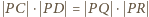 oraz
oraz 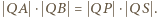 Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów
Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów 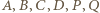 od punktu
od punktu 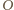 kolejno literami
kolejno literami 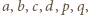 przepisujemy uzyskaną zależność w postaci
przepisujemy uzyskaną zależność w postaci 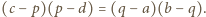 Po wymnożeniu i uwzględnieniu równości
Po wymnożeniu i uwzględnieniu równości 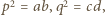 otrzymujemy związek
otrzymujemy związek 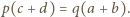 Tak więc
Tak więc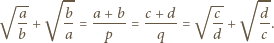
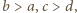 wynika stąd, że
wynika stąd, że 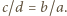 To zaś oznacza, że proste
To zaś oznacza, że proste 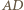 i
i 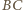 są równoległe.
są równoległe.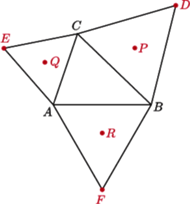
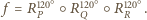 Na mocy
Na mocy 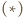 jest to przesunięcie. Ponieważ
jest to przesunięcie. Ponieważ 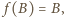 to wektor przesunięcia jest zerowy, czyli
to wektor przesunięcia jest zerowy, czyli 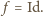 Zatem na mocy
Zatem na mocy 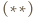 trójkąt
trójkąt 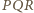 jest równoboczny.
jest równoboczny.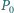 i trójkąt
i trójkąt 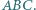 Niech
Niech 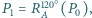
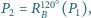
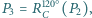
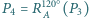 itd. Udowodnij, że jeżeli
itd. Udowodnij, że jeżeli 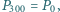 to trójkąt
to trójkąt 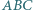 jest równoboczny.
jest równoboczny.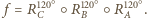 Na mocy
Na mocy 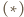 jest to przesunięcie. Z treści zadania wynika, że
jest to przesunięcie. Z treści zadania wynika, że 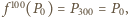 stąd wektor przesunięcia jest zerowy, czyli
stąd wektor przesunięcia jest zerowy, czyli 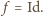 Wobec tego na mocy
Wobec tego na mocy 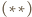 trójkąt
trójkąt 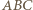 ma kąty równe
ma kąty równe 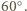
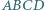 i
i 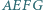 o środkach odpowiednio
o środkach odpowiednio 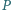 i
i 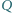 są tak samo zorientowane i mają rozłączne wnętrza. Punkty
są tak samo zorientowane i mają rozłączne wnętrza. Punkty 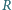 i
i 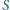 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 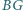 i
i 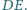 Wykaż, że czworokąt
Wykaż, że czworokąt 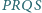 jest kwadratem.
jest kwadratem.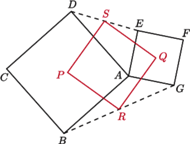
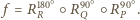 Na mocy
Na mocy 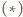 jest to przesunięcie;
jest to przesunięcie; 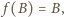 więc
więc 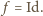 Na mocy
Na mocy 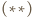 trójkąt
trójkąt 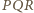 jest prostokątny i
jest prostokątny i 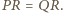 Tak samo dowodzimy, że trójkąt
Tak samo dowodzimy, że trójkąt 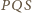 jest drugą połową kwadratu
jest drugą połową kwadratu 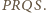
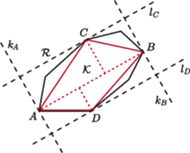
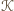 wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez
wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez 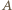 i
i 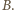 Przez te wierzchołki przeprowadźmy proste
Przez te wierzchołki przeprowadźmy proste 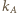 i
i 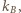 prostopadłe do odcinka
prostopadłe do odcinka 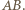 Wówczas
Wówczas 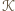 jest zawarty w pasie
jest zawarty w pasie 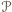 ograniczonym prostymi
ograniczonym prostymi 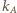 i
i 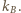 Po obu stronach prostej
Po obu stronach prostej 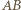 znajdźmy te wierzchołki
znajdźmy te wierzchołki 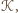 które są najdalej od tej prostej, i nazwijmy je
które są najdalej od tej prostej, i nazwijmy je 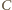 i
i 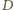 (być może któryś z nich jest wierzchołkiem
(być może któryś z nich jest wierzchołkiem 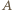 lub
lub 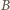 ). Przez
). Przez 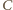 i
i 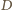 poprowadźmy proste
poprowadźmy proste 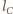 i
i 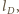 równoległe do
równoległe do 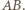 Wielokąt
Wielokąt 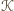 jest zawarty w pasie
jest zawarty w pasie 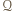 ograniczonym tymi prostymi, jest zatem zawarty w prostokącie
ograniczonym tymi prostymi, jest zatem zawarty w prostokącie 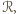 będącym przecięciem pasów
będącym przecięciem pasów 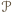 i
i 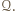 Z konstrukcji wynika, że pole prostokąta
Z konstrukcji wynika, że pole prostokąta 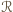 jest dwa razy większe od pola
jest dwa razy większe od pola 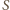 czworokąta
czworokąta 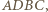 który jest zawarty w
który jest zawarty w 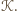 Zatem
Zatem 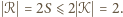
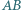 i
i 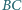 kwadratu
kwadratu 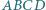 leżą (odpowiednio) takie punkty
leżą (odpowiednio) takie punkty 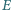 i
i 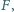 zaś wewnątrz tego kwadratu znajduje się taki punkt
zaś wewnątrz tego kwadratu znajduje się taki punkt 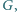 że
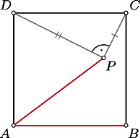
że 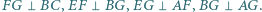 Sporządzony odręcznie rysunek sugeruje, że trapez
Sporządzony odręcznie rysunek sugeruje, że trapez 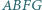 pokrywa około 40% powierzchni kwadratu
pokrywa około 40% powierzchni kwadratu 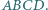 Czy jest to równość dokładna?
Czy jest to równość dokładna?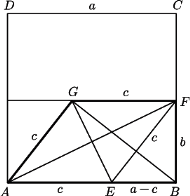
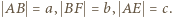 Z podanych warunków wynika, że czworokąt
Z podanych warunków wynika, że czworokąt 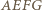 jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty
jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty 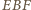 i
i 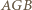 są podobne. Stąd
są podobne. Stąd 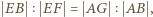 czyli
czyli 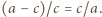 Z tego równania wyznaczamy
Z tego równania wyznaczamy 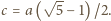 Z trójkąta prostokątnego
Z trójkąta prostokątnego 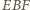 dostajemy
dostajemy 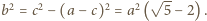 Pole trapezu
Pole trapezu 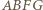 wynosi
wynosi 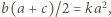 gdzie
gdzie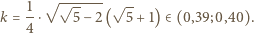
 punkty
punkty 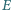 i
i 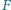 są środkami boków
są środkami boków 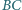 i
i 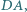 ponadto
ponadto 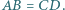 Wykaż, że prosta
Wykaż, że prosta 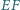 tworzy z prostymi
tworzy z prostymi 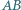 i
i 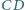 równe kąty.
równe kąty.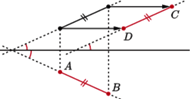
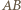 na
na 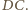 Na mocy
Na mocy 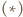 jej osią jest prosta
jej osią jest prosta 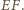 Prosta
Prosta 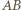 i jej obraz (prosta równoległa do
i jej obraz (prosta równoległa do 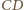 ) tworzą z osią symetrii równe kąty, co kończy dowód.
) tworzą z osią symetrii równe kąty, co kończy dowód.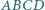 i
i 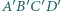 są przeciwnie zorientowane. Udowodnij, że środki odcinków
są przeciwnie zorientowane. Udowodnij, że środki odcinków 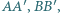
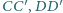 są współliniowe.
są współliniowe.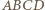 na
na 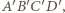 a następnie wykorzystać uwagę (*).
a następnie wykorzystać uwagę (*).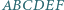 zachodzą równości
zachodzą równości 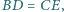
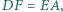
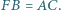 Wykaż, że symetralne boków
Wykaż, że symetralne boków  przecinają się w jednym punkcie.
przecinają się w jednym punkcie.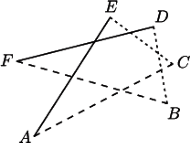
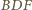 i
i 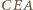 są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki
są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki 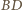 i
i 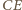 przecinają się, jako przekątne czworokąta wypukłego
przecinają się, jako przekątne czworokąta wypukłego 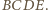 Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez
Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez 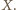
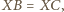 czyli punkt
czyli punkt 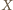 leży na symetralnej odcinka
leży na symetralnej odcinka 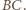 Analogicznie leży też na symetralnych
Analogicznie leży też na symetralnych 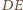 i
i 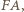 co kończy dowód.
co kończy dowód.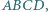 że
że 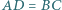 oraz boki
oraz boki 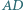 i
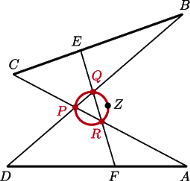
i 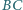 nie są równoległe. Zmienne punkty
nie są równoległe. Zmienne punkty 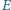 i
i 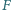 należą odpowiednio do boków
należą odpowiednio do boków 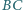 i
i 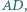 przy czym
przy czym 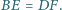 Proste
Proste 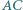 i
i 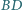 przecinają się w punkcie
przecinają się w punkcie 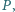 proste
proste 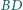 i
i 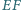 w punkcie
w punkcie 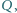 a proste
a proste 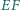 i
i 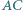 - w punkcie
- w punkcie 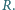 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach 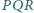 mają wspólny punkt różny od
mają wspólny punkt różny od 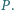
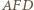 na
na 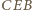 ; oznaczmy jego środek przez
; oznaczmy jego środek przez 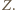 Podobnie jak w rozwiązaniu zadania 3, punkt
Podobnie jak w rozwiązaniu zadania 3, punkt 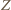 należy do symetralnych odcinków
należy do symetralnych odcinków 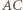 i
i 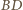 (a więc nie zależy od wyboru punktów
(a więc nie zależy od wyboru punktów 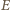 i
i 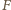 ) oraz do symetralnej
) oraz do symetralnej 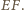 Stąd rzutami punktu
Stąd rzutami punktu 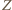 na odcinki
na odcinki 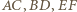 są ich środki.
są ich środki.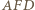 na
na 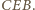 Na mocy (*), środki odcinków
Na mocy (*), środki odcinków 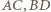 i
i 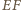 są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu
są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu 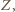 więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt
więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt  leży na każdym z okręgów opisanych na zmiennych trójkątach
leży na każdym z okręgów opisanych na zmiennych trójkątach 
 wybrano taki punkt
wybrano taki punkt 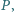 że
że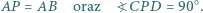
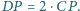
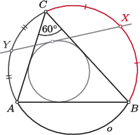
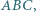 w którym
w którym 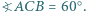 Na trójkącie tym opisano okrąg
Na trójkącie tym opisano okrąg 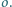 Punkt
Punkt 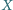 jest środkiem tego łuku
jest środkiem tego łuku 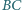 okręgu
okręgu 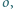 który nie zawiera punktu
który nie zawiera punktu 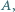 a punkt
a punkt 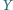 jest środkiem tego łuku
jest środkiem tego łuku 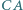 okręgu
okręgu 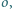 który nie zawiera punktu
który nie zawiera punktu 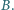 Udowodnij, że prosta
Udowodnij, że prosta 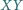 jest styczna do okręgu wpisanego w trójkąt
jest styczna do okręgu wpisanego w trójkąt 
 -kąta foremnego rozmieszczono liczby
-kąta foremnego rozmieszczono liczby 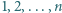 w taki sposób, że suma liczb znajdujących się w każdych trzech kolejnych wierzchołkach
w taki sposób, że suma liczb znajdujących się w każdych trzech kolejnych wierzchołkach  -kąta jest parzysta. Wyznacz wszystkie liczby naturalne
-kąta jest parzysta. Wyznacz wszystkie liczby naturalne 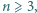 dla których takie rozmieszczenie jest możliwe.
dla których takie rozmieszczenie jest możliwe.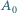 będzie ustalonym wierzchołkiem
będzie ustalonym wierzchołkiem 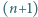 -kąta foremnego. Numerujemy pozostałe wierzchołki
-kąta foremnego. Numerujemy pozostałe wierzchołki 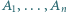 w dowolnej kolejności. Każdemu bokowi
w dowolnej kolejności. Każdemu bokowi 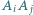 przyporządkowujemy liczbę
przyporządkowujemy liczbę 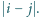 Niech
Niech 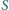 będzie sumą
będzie sumą 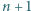 liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej
liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej  :
: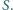
 wierzchołków (poza
wierzchołków (poza 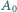 ), przy których
), przy których 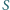 osiąga ową minimalną wartość.
osiąga ową minimalną wartość.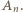 Idąc od
Idąc od 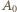 do
do 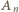 wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki
wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki 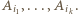 Przechodzimy przez
Przechodzimy przez 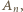 dalej mijamy wierzchołki
dalej mijamy wierzchołki 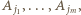 i wracamy do
i wracamy do 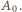 Numery
Numery 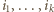 oraz
oraz 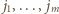 tworzą permutację zbioru
tworzą permutację zbioru 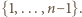 Liczby, przyporządkowane wszystkim bokom, sumują się do wartości
Liczby, przyporządkowane wszystkim bokom, sumują się do wartości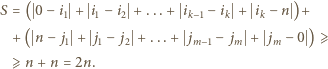
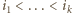 oraz
oraz 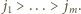 Zatem
Zatem 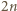 to szukane minimum.
to szukane minimum.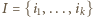 może być dowolnym podzbiorem zbioru
może być dowolnym podzbiorem zbioru 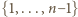 (również pustym, wtedy pierwszy składnik rozpisanej sumy
(również pustym, wtedy pierwszy składnik rozpisanej sumy 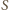 ma postać
ma postać 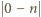 ). Zauważmy teraz, że już sam wybór zbioru
). Zauważmy teraz, że już sam wybór zbioru 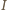 determinuje ponumerowanie, realizujące równość
determinuje ponumerowanie, realizujące równość 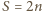 ; liczby ze zbioru
; liczby ze zbioru 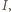 uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od
uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od 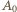 w wybranym kierunku), następny wierzchołek trzeba nazwać
w wybranym kierunku), następny wierzchołek trzeba nazwać 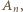 a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.
a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.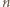 wierzchołków, ile podzbiorów ma zbiór
wierzchołków, ile podzbiorów ma zbiór 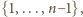 to znaczy
to znaczy 
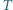 jest wpisany w okrąg
jest wpisany w okrąg 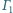 oraz opisany na okręgu
oraz opisany na okręgu 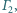 przy czym
przy czym 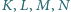 są kolejnymi punktami styczności
są kolejnymi punktami styczności 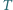 z
z 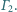 Wykaż, że
Wykaż, że 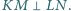
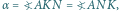
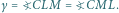
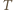 jest wpisany w okrąg, to
jest wpisany w okrąg, to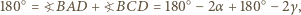
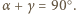
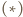 dla okręgu
dla okręgu 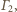 mamy
mamy 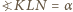 oraz
oraz 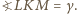 Wobec tego
Wobec tego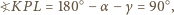
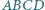 i taki punkt
i taki punkt 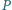 w jego wnętrzu, dla którego
w jego wnętrzu, dla którego 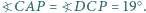 Wyznacz
Wyznacz 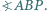
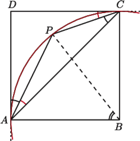
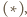 prosta
prosta 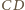 jest styczna do okręgu opisanego na trójkącie
jest styczna do okręgu opisanego na trójkącie 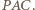 Wobec tego środek tego okręgu leży na prostej
Wobec tego środek tego okręgu leży na prostej 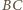 (bo
(bo 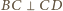 ). Analogicznie prosta
). Analogicznie prosta 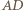 także jest styczna do tego okręgu, gdyż
także jest styczna do tego okręgu, gdyż 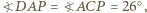 zatem środek rozważanego okręgu leży też na prostej
zatem środek rozważanego okręgu leży też na prostej 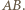 Stąd jest nim punkt
Stąd jest nim punkt 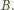
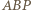 jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany
jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany 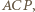 zatem
zatem 
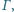 wpisany w trójkąt
wpisany w trójkąt 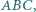 jest styczny do boków
jest styczny do boków 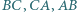 odpowiednio w punktach
odpowiednio w punktach 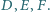 Wykaż, że środki
Wykaż, że środki 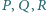 okręgów wpisanych w trójkąty
okręgów wpisanych w trójkąty 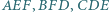 leżą na okręgu
leżą na okręgu 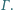
 okręgu
okręgu  przez
przez 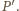 Wówczas
Wówczas 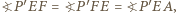 przy czym druga równość wynika z twierdzenia
przy czym druga równość wynika z twierdzenia 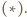 Wobec tego
Wobec tego 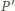 leży na dwusiecznej kąta
leży na dwusiecznej kąta 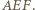 Analogicznie dla kąta
Analogicznie dla kąta 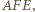 więc
więc 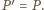 Dowód dla punktów
Dowód dla punktów 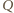 i
i 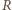 przebiega podobnie.
przebiega podobnie.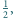 a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.
a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.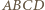 i w nim trójkąt
i w nim trójkąt 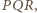 którego wierzchołki leżą na różnych bokach kwadratu tak, że
którego wierzchołki leżą na różnych bokach kwadratu tak, że 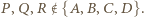 Wówczas trójkąt
Wówczas trójkąt 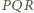 łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (
łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (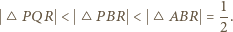


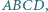 w którym kąty wewnętrzne przy wierzchołkach
w którym kąty wewnętrzne przy wierzchołkach 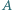 oraz
oraz 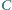 są równe, przy tym ostre. Punkty
są równe, przy tym ostre. Punkty 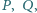 leżące odpowiednio na półprostych
leżące odpowiednio na półprostych 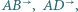 są wyznaczone przez warunki
są wyznaczone przez warunki 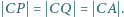 Wykazać, że długość odcinka
Wykazać, że długość odcinka 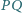 nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 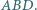
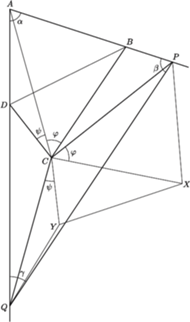
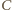 leży wewnątrz trójkąta
leży wewnątrz trójkąta 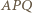 (jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego
(jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego 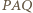 ). Oznaczmy kąty tego trójkąta:
). Oznaczmy kąty tego trójkąta: 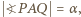
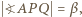
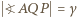 ; ponadto niech
; ponadto niech 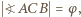
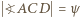 ; z założenia
; z założenia 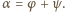
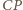 i
i  czworokąta (wklęsłego)
czworokąta (wklęsłego) 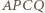 budujemy, po zewnętrznej jego stronie, trójkąty
budujemy, po zewnętrznej jego stronie, trójkąty 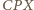 i
i 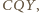 przystające odpowiednio do trójkątów
przystające odpowiednio do trójkątów 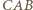 i
i 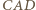 :
: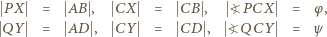
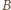 leży między
leży między 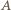 i
i 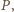 zaś
zaś 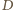 między
między 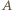 i
i 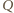 ; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro
; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro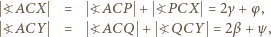
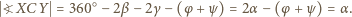
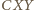 jest przystający do trójkąta
jest przystający do trójkąta 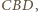 wobec czego
wobec czego 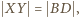 i otrzymujemy tezę zadania:
i otrzymujemy tezę zadania: