Kochajcie trygonometrię, dziewczęta»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Kochajcie trygonometrię, dziewczęta
- Publikacja w Delcie: luty 2020
- Publikacja elektroniczna: 1 lutego 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Punkt 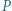 leży na boku
leży na boku 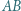 trójkąta
trójkąta 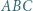 . Niech
. Niech 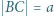 ,
, 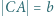 ,
, 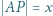 i
i 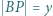 . Dowieść, że
. Dowieść, że 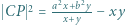 (twierdzenie Stewarta).
(twierdzenie Stewarta).
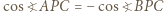 . Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio
. Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio 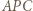 i
i 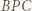 , a następnie przekształcić otrzymaną równość, by otrzymać
, a następnie przekształcić otrzymaną równość, by otrzymać 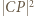 .
.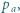
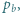
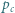 i
i 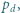 mające wspólny początek
mające wspólny początek 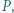 które zostały podane w kolejności antyzegarowej. Prosta
które zostały podane w kolejności antyzegarowej. Prosta 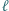 przecina je odpowiednio w punktach
przecina je odpowiednio w punktach 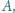
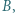
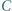 i
i 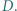 Dowieść, że wartość wyrażenia
Dowieść, że wartość wyrażenia 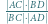 nie zależy od wyboru prostej
nie zależy od wyboru prostej 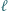 (niezmienniczość dwustosunku).
(niezmienniczość dwustosunku).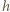 będzie odległością punktu
będzie odległością punktu 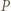 od prostej
od prostej 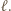 Oznaczmy przez
Oznaczmy przez 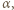
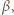
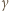 kąty pomiędzy półprostymi odpowiednio
kąty pomiędzy półprostymi odpowiednio 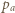 i
i 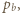
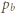 i
i 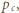
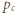 i
i 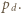 Wówczas obliczając na dwa sposoby pole trójkąta
Wówczas obliczając na dwa sposoby pole trójkąta 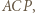 otrzymamy
otrzymamy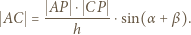
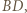
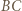 i
i 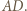
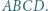 Punkty
Punkty 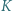 i
i 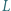 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 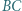 i
i 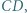 przy czym trójkąt
przy czym trójkąt 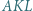 jest równoboczny. Dowieść, że suma pól trójkątów
jest równoboczny. Dowieść, że suma pól trójkątów 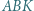 i
i 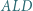 jest równa polu trójkąta
jest równa polu trójkąta 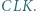
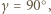 to
to ![1 [ABC] = 4 c2sin2α .](/math/temat/matematyka/geometria/zadania/2020/01/29/zm-20-02-kpo-4/2x-d78da09147956ae846d84f71c06c7431235d18c7-im-66,57,43-FF,FF,FF.gif) Niech
Niech 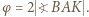 Zadanie sprowadza się do wykazania równości
Zadanie sprowadza się do wykazania równości 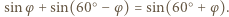
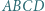 wpisany jest w okrąg. Na tym okręgu leży punkt
wpisany jest w okrąg. Na tym okręgu leży punkt 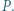 Udowodnić, że iloczyn odległości punktu
Udowodnić, że iloczyn odległości punktu 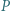 od prostych
od prostych 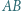 i
i 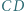 jest równy iloczynowi odległości punktu
jest równy iloczynowi odległości punktu 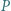 od prostych
od prostych 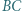 i
i 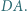
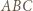 opuszczona z wierzchołka
opuszczona z wierzchołka 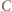 ma długość
ma długość 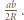 Odległości punktu
Odległości punktu 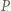 od prostych
od prostych 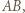
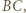
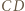 i
i 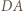 są odpowiednio wysokościami trójkątów
są odpowiednio wysokościami trójkątów 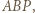
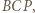
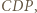
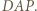
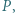
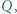
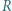 leżą odpowiednio na bokach
leżą odpowiednio na bokach 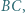
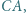
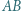 trójkąta
trójkąta 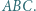 Spełnione są następujące równości:
Spełnione są następujące równości:
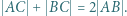
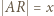 i
i 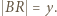 Obliczając pole trójkąta
Obliczając pole trójkąta  na dwa sposoby, otrzymamy równość
na dwa sposoby, otrzymamy równość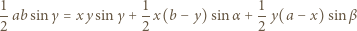
 i uprościć tę równość.
i uprościć tę równość. zachodzą następujące równości:
zachodzą następujące równości: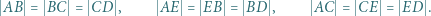
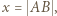
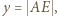
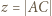 oraz
oraz 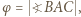
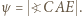 Z równości
Z równości 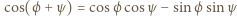 otrzymamy po przekształceniach
otrzymamy po przekształceniach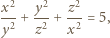
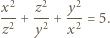
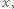
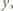
 są równe, a dzięki założeniu o wypukłości pięciokąta mamy
są równe, a dzięki założeniu o wypukłości pięciokąta mamy 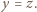 Dalszą część rozwiązania stanowią proste rachunki na kątach.
Dalszą część rozwiązania stanowią proste rachunki na kątach.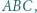 wpisanym w okrąg o środku
wpisanym w okrąg o środku 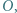 kąt przy wierzchołku
kąt przy wierzchołku 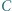 jest rozwarty oraz zachodzi równość
jest rozwarty oraz zachodzi równość 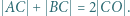 Odcinki
Odcinki 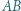 i
i 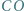 przecinają się w punkcie
przecinają się w punkcie 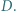 Dwusieczne kątów
Dwusieczne kątów 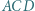 i
i 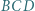 przecinają odcinek
przecinają odcinek 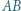 w punktach odpowiednio
w punktach odpowiednio 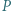 i
i 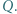 Dowieść, że punkt
Dowieść, że punkt 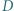 jest środkiem odcinka
jest środkiem odcinka 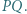
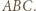 Z twierdzenia o dwusiecznej zastosowanego dla trójkąta
Z twierdzenia o dwusiecznej zastosowanego dla trójkąta 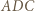 otrzymujemy
otrzymujemy 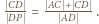 Miary kątów trójkąta
Miary kątów trójkąta 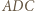 wynoszą odpowiednio
wynoszą odpowiednio 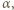
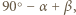
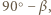 więc z twierdzenia sinusów
więc z twierdzenia sinusów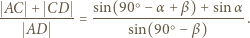
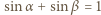 (treść zadania + twierdzenie sinusów), otrzymamy
(treść zadania + twierdzenie sinusów), otrzymamy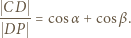
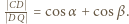
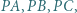 gdzie
gdzie 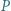 jest punktem wewnątrz trójkąta równobocznego
jest punktem wewnątrz trójkąta równobocznego 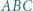 o boku 1.
o boku 1.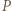 poprowadźmy proste równoległe do boków trójkąta
poprowadźmy proste równoległe do boków trójkąta 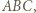 przecinające te boki w punktach
przecinające te boki w punktach 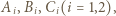 jak na rysunku. Wówczas
jak na rysunku. Wówczas 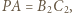 podobnie z długościami
podobnie z długościami 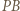 i
i 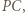 stąd należy zmaksymalizować pole trójkąta
stąd należy zmaksymalizować pole trójkąta 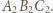 Oznaczając przez
Oznaczając przez ![[ |ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/8x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) pole figury
pole figury 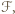 dostajemy
dostajemy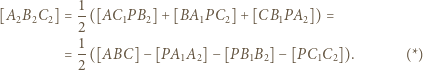
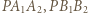 i
i 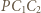 są podobne do
są podobne do 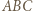 w skalach odpowiednio
w skalach odpowiednio 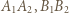 i
i 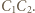 W związku z tym
W związku z tym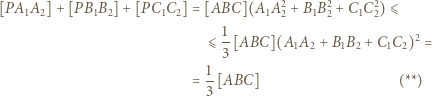
![|[A2B2C2]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/17x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) Równość otrzymamy, biorąc za punkt
Równość otrzymamy, biorąc za punkt 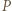 środek ciężkości trójkąta
środek ciężkości trójkąta  co kończy rozwiązanie.
co kończy rozwiązanie.
 można wpisać okrąg. Przez środek każdego z odcinków
można wpisać okrąg. Przez środek każdego z odcinków  poprowadzono proste prostopadłe do przeciwległych boków czworokąta
poprowadzono proste prostopadłe do przeciwległych boków czworokąta 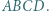 Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
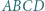 można opisać okrąg. Niech
można opisać okrąg. Niech 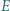 będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta
będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta 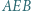 przecina prostą
przecina prostą 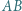 w punkcie
w punkcie 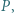 zaś prostą
zaś prostą 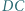 w punkcie
w punkcie 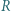 ; niech ponadto dwusieczna kąta
; niech ponadto dwusieczna kąta 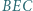 przecina prostą
przecina prostą 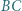 w punkcie
w punkcie 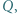 zaś prostą
zaś prostą 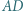 w punkcie
w punkcie 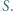 Udowodnić, że okręgi opisane na trójkątach
Udowodnić, że okręgi opisane na trójkątach 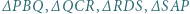 mają punkt wspólny.
mają punkt wspólny.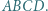 Punkty
Punkty 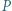 i
i 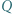 leżące odpowiednio wewnątrz trójkątów
leżące odpowiednio wewnątrz trójkątów 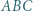 i
i 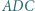 mają tę własność, że
mają tę własność, że 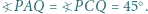 Wykazać, że
Wykazać, że
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-36c19e6efa8cca90b4ecde58a9ea9c818585cc21-im-2C,6B,73-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 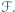
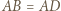 oraz
oraz 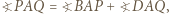 to istnieje punkt jednocześnie symetryczny do
to istnieje punkt jednocześnie symetryczny do 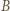 względem
względem 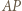 i do
i do 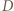 względem
względem 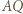 ; nazwijmy go
; nazwijmy go 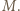 Skoro
Skoro ![|[ABP P]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![QQ]], |[AD](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/9x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif) to lewa strona dowodzonej równości przybiera postać
to lewa strona dowodzonej równości przybiera postać 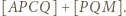
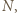 jednocześnie symetryczny do
jednocześnie symetryczny do 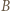 względem
względem 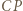 oraz do
oraz do 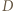 względem
względem 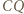 i podobnie prawą stronę dowodzonej równości można przepisać jako
i podobnie prawą stronę dowodzonej równości można przepisać jako 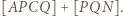 Do zakończenia rozwiązania wystarczy zauważyć, że trójkąty
Do zakończenia rozwiązania wystarczy zauważyć, że trójkąty 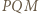 oraz
oraz 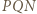 są przystające (cecha bok-bok-bok).
są przystające (cecha bok-bok-bok).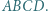 Punkty
Punkty 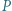 i
i 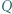 leżące odpowiednio wewnątrz trójkątów
leżące odpowiednio wewnątrz trójkątów 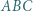 i
i 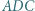 mają tę własność, że
mają tę własność, że 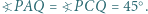 Wykazać, że
Wykazać, że 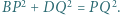
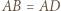 oraz
oraz 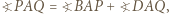 to istnieje punkt jednocześnie symetryczny do
to istnieje punkt jednocześnie symetryczny do 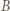 względem
względem 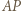 i do
i do 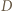 względem
względem 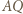 ; nazwijmy go
; nazwijmy go 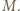 Trójkąt
Trójkąt 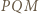 ma boki o długościach
ma boki o długościach 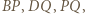 a jego kąt wewnętrzny przy wierzchołku
a jego kąt wewnętrzny przy wierzchołku 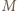 ma miarę
ma miarę 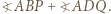
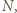 jednocześnie symetryczny do
jednocześnie symetryczny do 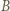 względem
względem 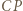 oraz do
oraz do 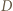 względem
względem 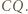 Trójkąt
Trójkąt 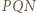 jest przystający do trójkąta
jest przystający do trójkąta 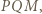 a kąt wewnętrzny przy wierzchołku
a kąt wewnętrzny przy wierzchołku 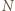 ma miarę
ma miarę 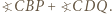 Pozostaje zauważyć, że
Pozostaje zauważyć, że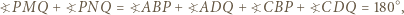
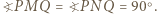 Teza zadania wynika więc z twierdzenia Pitagorasa zastosowanego do dowolnego z tych dwóch trójkątów.
Teza zadania wynika więc z twierdzenia Pitagorasa zastosowanego do dowolnego z tych dwóch trójkątów.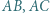 trójkąta ostrokątnego
trójkąta ostrokątnego 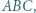 po jego zewnętrznej stronie, zbudowano trójkąty prostokątne równoramienne
po jego zewnętrznej stronie, zbudowano trójkąty prostokątne równoramienne 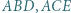 z kątami prostymi przy wierzchołkach
z kątami prostymi przy wierzchołkach 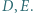 Odcinki
Odcinki 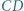 i
i 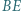 przecinają się w punkcie
przecinają się w punkcie 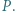 Punkty
Punkty 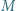 i
i 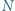 są środkami odcinków
są środkami odcinków 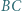 i
i 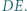 Udowodnić, że każda z prostych
Udowodnić, że każda z prostych 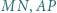 jest prostopadła do prostej
jest prostopadła do prostej 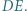
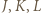 będą rzutami prostokątnymi punktów
będą rzutami prostokątnymi punktów 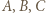 na prostą
na prostą 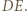 Trójkąt prostokątny
Trójkąt prostokątny 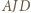 jest przystający do trójkąta
jest przystający do trójkąta 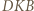 ; analogicznie, trójkąt
; analogicznie, trójkąt 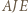 przystaje do
przystaje do 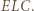 Zatem
Zatem 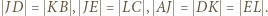 Z ostatniej równości wynika, że środek
Z ostatniej równości wynika, że środek 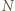 odcinka
odcinka 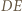 jest też środkiem odcinka
jest też środkiem odcinka 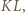 i wobec tego
i wobec tego 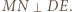
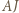 przecina odcinki
przecina odcinki 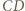 i
i 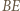 w punktach, które nazwiemy odpowiednio
w punktach, które nazwiemy odpowiednio 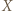 i
i 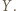 Z proporcji
Z proporcji

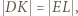 zatem
zatem 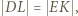 i w takim razie
i w takim razie 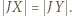 To oznacza, że
To oznacza, że 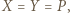 a prosta
a prosta 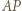 to prosta
to prosta 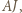 prostopadła (z definicji) do
prostopadła (z definicji) do 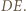
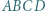 o podstawach
o podstawach 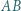 i
i 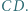 Okręgi o średnicach
Okręgi o średnicach 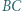 i
i 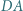 przecinają się w punktach
przecinają się w punktach 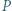 i
i 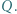 Przekątne trapezu przecinają się w punkcie
Przekątne trapezu przecinają się w punkcie 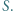 Dowieść, że punkty
Dowieść, że punkty 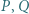 i
i 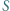 leżą na jednej prostej.
leżą na jednej prostej.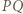 jest osią potęgową pary okręgów z zadania, więc wystarczy wykazać, że punkt
jest osią potęgową pary okręgów z zadania, więc wystarczy wykazać, że punkt 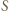 ma jednakową względem nich potęgę. Można to zrobić za pomocą podobieństwa trójkątów
ma jednakową względem nich potęgę. Można to zrobić za pomocą podobieństwa trójkątów 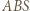 i
i 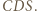
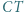 jest wysokością trójkąta
jest wysokością trójkąta 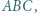 w którym
w którym 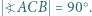 Okrąg o środku
Okrąg o środku 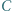 i promieniu
i promieniu 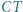 oraz okrąg opisany na trójkącie
oraz okrąg opisany na trójkącie 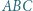 przecinają się w punktach
przecinają się w punktach 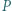 i
i 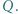 Dowieść, że prosta
Dowieść, że prosta 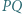 przechodzi przez środek odcinka
przechodzi przez środek odcinka 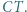
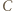 ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.
ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.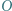 jest środkiem okręgu opisanego, a punkt
jest środkiem okręgu opisanego, a punkt 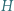 ortocentrum trójkąta ostrokątnego i różnobocznego
ortocentrum trójkąta ostrokątnego i różnobocznego 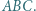 Punkty
Punkty 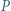 i
i 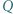 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 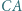 i
i 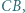 przy czym czworokąt
przy czym czworokąt 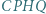 jest równoległobokiem. Wykazać, że
jest równoległobokiem. Wykazać, że 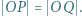
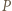 i
i 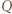 mają równą potęgę względem okręgu opisanego na trójkącie
mają równą potęgę względem okręgu opisanego na trójkącie 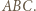 Do tego celu wystarczy podobieństwo odpowiednich trójkątów.
Do tego celu wystarczy podobieństwo odpowiednich trójkątów.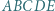 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 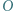 ; przy tym
; przy tym 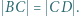 Przekątne
Przekątne 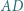 i
i 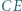 są prostopadłe, zaś przekątne
są prostopadłe, zaś przekątne 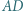 i
i 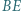 przecinają się w takim punkcie
przecinają się w takim punkcie 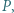 że
że 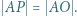 Wykazać, że trójkąt
Wykazać, że trójkąt 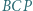 jest równoboczny.
jest równoboczny.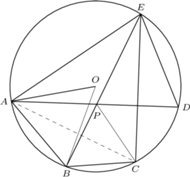
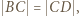 punkt
punkt 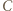 jest środkiem łuku
jest środkiem łuku 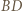 ; zatem prosta
; zatem prosta 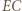 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 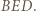 Przy tym jest prostopadła do prostej
Przy tym jest prostopadła do prostej 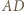 ; jest więc symetralną odcinka
; jest więc symetralną odcinka 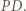 Stąd wynika, że
Stąd wynika, że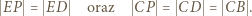
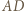 i
i 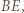 przecinające się w punkcie
przecinające się w punkcie 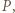 wyznaczają trójkąty podobne:
wyznaczają trójkąty podobne: 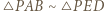 ; a ponieważ
; a ponieważ 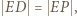 zatem
zatem 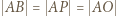 (ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 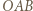 jest równoboczny, wobec czego
jest równoboczny, wobec czego 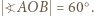 W takim razie
W takim razie 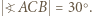
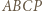 to deltoid
to deltoid 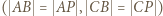 ; stąd
; stąd 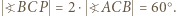 Wobec wcześniejszego spostrzeżenia, że
Wobec wcześniejszego spostrzeżenia, że 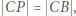 dostajemy tezę zadania: trójkąt
dostajemy tezę zadania: trójkąt 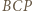 jest równoboczny.
jest równoboczny.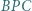 i
i 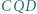 są równoboczne i leżą na zewnątrz równoległoboku
są równoboczne i leżą na zewnątrz równoległoboku 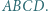 Udowodnić, że trójkąt
Udowodnić, że trójkąt 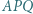 też jest równoboczny.
też jest równoboczny.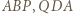 i
i 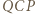 są przystające (bkb).
są przystające (bkb).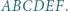 Punkty
Punkty 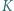 i
i 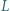 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 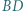 i
i 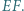 Dowieść, że trójkąt
Dowieść, że trójkąt 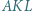 jest równoboczny.
jest równoboczny.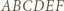 na
na 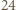 przystające trójkąty równoboczne można zauważyć, że odcinki
przystające trójkąty równoboczne można zauważyć, że odcinki 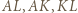 są dłuższymi przekątnymi przystających równoległoboków
są dłuższymi przekątnymi przystających równoległoboków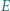 i
i 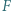 leżą odpowiednio na bokach
leżą odpowiednio na bokach 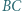 i
i 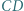 prostokąta
prostokąta 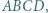 przy czym trójkąt
przy czym trójkąt 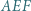 jest równoboczny. Punkt
jest równoboczny. Punkt 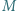 jest środkiem odcinka
jest środkiem odcinka 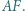 Wykazać, że trójkąt
Wykazać, że trójkąt 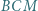 jest równoboczny.
jest równoboczny.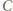 i
i 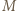 leżą na okręgu o średnicy
leżą na okręgu o średnicy 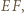 więc
więc 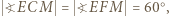 analogicznie
analogicznie