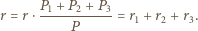Czy aby na pewno?»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Czy aby na pewno?
- Publikacja w Delcie: lipiec 2016
- Publikacja elektroniczna: 1 lipca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (42 KB)
Pewien sześciokąt wypukły ma wszystkie kąty równe 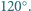 Czy wynika z tego, że jest on foremny?
Czy wynika z tego, że jest on foremny?
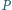 leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 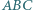 oraz
oraz 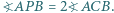 Czy wynika z tego, że
Czy wynika z tego, że 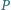 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 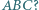
 boków. Czy wynika z tego, że ściana ta graniczy z
boków. Czy wynika z tego, że ściana ta graniczy z  innymi ścianami tego wielościanu?
innymi ścianami tego wielościanu?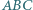 kąt przy wierzchołku
kąt przy wierzchołku 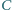 ma miarę
ma miarę 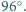 Wewnątrz trójkąta leży taki punkt
Wewnątrz trójkąta leży taki punkt 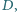 że
że 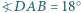 i
i 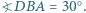 Wyznaczyć miarę kąta
Wyznaczyć miarę kąta 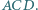
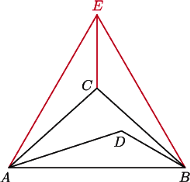
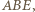 że punkt
że punkt 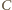 leży w jego wnętrzu. Wówczas punkty
leży w jego wnętrzu. Wówczas punkty 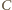 i
i 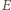 leżą na symetralnej odcinka
leżą na symetralnej odcinka 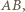 więc
więc 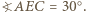 Ponadto
Ponadto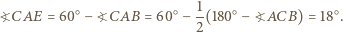
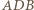 i
i 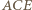 są przystające, w szczególności
są przystające, w szczególności 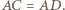 Stąd łatwo otrzymujemy
Stąd łatwo otrzymujemy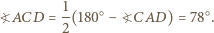
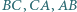 trójkąta
trójkąta 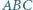 leżą punkty
leżą punkty 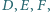 w których okręgi dopisane do trójkąta są styczne do tych boków. Niech
w których okręgi dopisane do trójkąta są styczne do tych boków. Niech 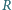 i
i  będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów
będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów 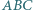 i
i 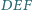 wynosi
wynosi 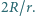
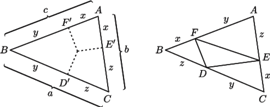
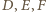 są położone na bokach
są położone na bokach 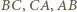 symetrycznie (względem środków owych boków) do punktów
symetrycznie (względem środków owych boków) do punktów 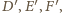 w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia:
w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia: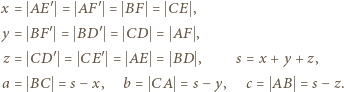
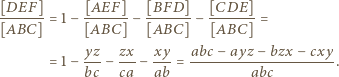
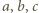 przez
przez 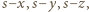 otrzymujemy po krótkim rachunku wzór
otrzymujemy po krótkim rachunku wzór![EF] [D----- 2xyz- [ABC]= abc .](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/4x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
 i
i 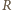 to promienie okręgów wpisanego i opisanego):
to promienie okręgów wpisanego i opisanego):![[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/7x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
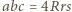 oraz
oraz 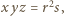 które po wprowadzeniu do równości
które po wprowadzeniu do równości 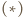 dają tezę zadania.
dają tezę zadania.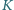 i
i 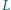 są środkami odpowiednio boków
są środkami odpowiednio boków 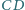 i
i 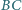 równoległoboku
równoległoboku 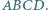 Udowodnij, że odcinki
Udowodnij, że odcinki 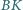 i
i 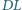 przecinają się na przekątnej
przecinają się na przekątnej 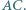

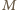 będzie punktem przecięcia przekątnych danego równoległoboku. Wówczas
będzie punktem przecięcia przekątnych danego równoległoboku. Wówczas 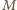 jest środkiem odcinka
jest środkiem odcinka 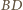 i odcinki
i odcinki 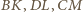 przecinają się w jednym punkcie jako środkowe trójkąta
przecinają się w jednym punkcie jako środkowe trójkąta 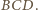
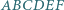 jest wpisany w okrąg i
jest wpisany w okrąg i 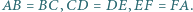 Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
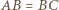 wynika, że punkt
wynika, że punkt 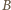 jest środkiem łuku
jest środkiem łuku 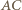 danego okręgu i kąty wpisane
danego okręgu i kąty wpisane 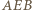 i
i 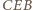 są równe. Prosta
są równe. Prosta 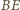 jest więc dwusieczną kąta
jest więc dwusieczną kąta 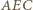 w trójkącie
w trójkącie 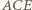 ; analogicznie proste
; analogicznie proste 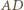 i
i 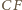 są dwusiecznymi pozostałych kątów tego trójkąta.
są dwusiecznymi pozostałych kątów tego trójkąta.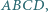 w którym
w którym 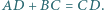 Dwusieczne kątów
Dwusieczne kątów 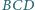 i
i 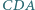 przecinają się w punkcie
przecinają się w punkcie 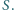 Udowodnij, że
Udowodnij, że 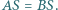

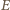 będzie takim punktem boku
będzie takim punktem boku 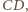 że
że 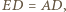 wtedy
wtedy 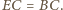 Wówczas punkty
Wówczas punkty 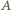 i
i 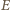 są symetryczne względem dwusiecznej kąta
są symetryczne względem dwusiecznej kąta 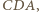 zatem prosta
zatem prosta 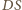 jest symetralną odcinka
jest symetralną odcinka 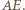 Analogicznie prosta
Analogicznie prosta 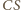 jest symetralną odcinka
jest symetralną odcinka 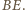 Symetralne boków trójkąta
Symetralne boków trójkąta 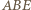 przecinają się w punkcie
przecinają się w punkcie 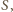 a stąd
a stąd 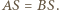
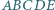 są równe. Symetralne odcinków
są równe. Symetralne odcinków 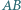 i
i  przecinają się w punkcie
przecinają się w punkcie 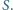 Wykaż, że proste
Wykaż, że proste 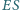 i
i 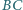 są prostopadłe.
są prostopadłe.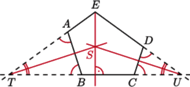
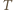 i
i 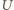 będą punktami przecięcia prostej
będą punktami przecięcia prostej 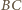 odpowiednio z prostymi
odpowiednio z prostymi 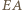 i
i 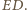 Wobec równości kątów, trójkąty
Wobec równości kątów, trójkąty 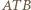 i
i 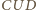 są równoramienne i podobne, a stąd
są równoramienne i podobne, a stąd 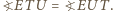 Symetralna boku
Symetralna boku 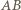 jest jednocześnie dwusieczną kąta przy wierzchołku
jest jednocześnie dwusieczną kąta przy wierzchołku 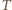 w trójkącie
w trójkącie 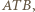 a więc także w trójkącie
a więc także w trójkącie 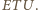 Podobnie symetralna odcinka
Podobnie symetralna odcinka 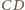 jest dwusieczną kąta
jest dwusieczną kąta 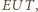 zatem
zatem 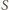 jest punktem przecięcia dwusiecznych trójkąta równoramiennego
jest punktem przecięcia dwusiecznych trójkąta równoramiennego 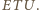 Dwusieczna
Dwusieczna 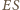 jest więc prostopadła do podstawy
jest więc prostopadła do podstawy 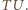
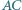 i
i 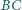 trójkąta
trójkąta 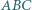 zbudowano, na zewnątrz, kwadraty
zbudowano, na zewnątrz, kwadraty 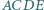 i
i 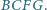 Udowodnij, że proste
Udowodnij, że proste 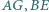 oraz wysokość
oraz wysokość 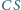 trójkąta
trójkąta 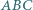 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.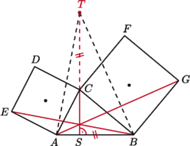
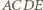 o
o 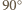 wokół środka tak, by punkt
wokół środka tak, by punkt 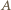 przeszedł na punkt
przeszedł na punkt 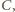 natomiast kwadrat
natomiast kwadrat 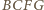 o
o 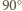 wokół swojego środka tak, by punkt
wokół swojego środka tak, by punkt 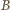 przeszedł na punkt
przeszedł na punkt 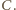 Przy obydwu tych obrotach odcinek
Przy obydwu tych obrotach odcinek 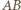 przechodzi na ten sam odcinek o końcu w punkcie
przechodzi na ten sam odcinek o końcu w punkcie 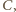 prostopadły do
prostopadły do 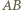 i równy
i równy 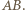 Nazwijmy drugi jego koniec
Nazwijmy drugi jego koniec 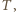 wówczas punkty
wówczas punkty 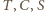 są współliniowe.
są współliniowe.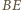 przechodzi na
przechodzi na 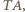 stąd
stąd 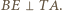 Przy drugim obrocie odcinek
Przy drugim obrocie odcinek 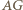 przechodzi na
przechodzi na 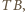 zatem
zatem 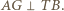 Wobec tego proste
Wobec tego proste 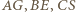 są wysokościami trójkąta
są wysokościami trójkąta 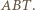
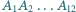 przekątne
przekątne 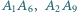 i
i 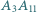 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.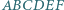 jest równa
jest równa 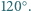 Udowodnij, że symetralne odcinków
Udowodnij, że symetralne odcinków 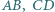 i
i 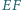 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.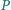 leży wewnątrz trójkąta
leży wewnątrz trójkąta 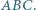 Punkty
Punkty 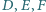 to punkty symetryczne do punktu
to punkty symetryczne do punktu 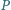 odpowiednio względem prostych
odpowiednio względem prostych 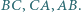 Wykaż, że jeśli trójkąt
Wykaż, że jeśli trójkąt 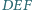 jest równoboczny, to proste
jest równoboczny, to proste 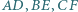 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.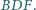
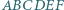 jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że
jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że 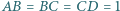 oraz
oraz 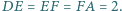
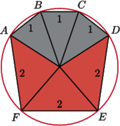
 jak na rysunku.
jak na rysunku.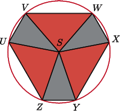
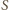 oznacza środek okręgu opisanego na sześciokącie
oznacza środek okręgu opisanego na sześciokącie 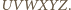 Z przystawania czworokątów
Z przystawania czworokątów 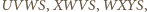
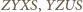 i
i 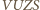 wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po
wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po 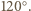 Z twierdzenia cosinusów dla trójkąta
Z twierdzenia cosinusów dla trójkąta 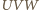 otrzymujemy
otrzymujemy 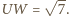 Trójkąt
Trójkąt 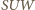 jest trójkątem równoramiennym o kącie
jest trójkątem równoramiennym o kącie 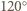 w wierzchołku
w wierzchołku 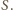 Stąd możemy obliczyć szukany promień, równy
Stąd możemy obliczyć szukany promień, równy 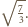
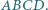 Proste zawierające dwusieczne kątów wewnętrznych
Proste zawierające dwusieczne kątów wewnętrznych 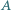 i
i 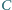 przecinają się w punkcie
przecinają się w punkcie 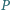 leżącym wewnątrz czworokąta
leżącym wewnątrz czworokąta 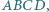 a proste zawierające dwusieczne kątów wewnętrznych
a proste zawierające dwusieczne kątów wewnętrznych 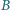 i
i 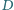 przecinają się w punkcie
przecinają się w punkcie 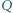 na zewnątrz czworokąta. Udowodnij, że jeżeli kąt
na zewnątrz czworokąta. Udowodnij, że jeżeli kąt 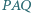 jest prosty, to również kąt
jest prosty, to również kąt 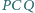 jest prosty.
jest prosty.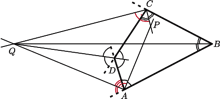
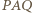 jest prosty, to
jest prosty, to 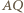 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 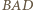 czworokąta. Z kolei aby dowieść, że kąt
czworokąta. Z kolei aby dowieść, że kąt 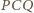 jest prosty, wystarczy wykazać, że
jest prosty, wystarczy wykazać, że 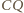 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 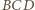 czworokąta.
czworokąta.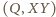 odległość punktu
odległość punktu 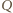 od prostej
od prostej 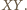 Zachodzą równości
Zachodzą równości 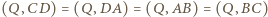 oraz
oraz 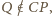 co kończy dowód.
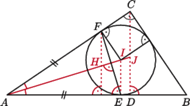
co kończy dowód.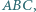 w którym kąt przy wierzchołku
w którym kąt przy wierzchołku 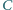 jest prosty. Punkt
jest prosty. Punkt 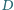 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 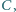 a okrąg wpisany w dany trójkąt jest styczny do boków
a okrąg wpisany w dany trójkąt jest styczny do boków 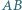 i
i 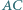 odpowiednio w punktach
odpowiednio w punktach 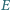 i
i 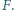 Wykaż, że ortocentrum trójkąta
Wykaż, że ortocentrum trójkąta 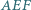 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 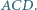
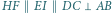
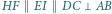
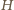 ortocentrum trójkąta
ortocentrum trójkąta 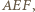 przez
przez 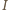 środek okręgu wpisanego w trójkąt
środek okręgu wpisanego w trójkąt 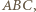 a przez
a przez 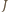 punkt przecięcia prostych
punkt przecięcia prostych 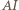 i
i 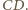 Ponieważ
Ponieważ 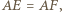 więc półprosta
więc półprosta 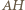 jest dwusieczną kąta
jest dwusieczną kąta 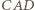 i do zakończenia dowodu wystarczy wykazać, że półprosta
i do zakończenia dowodu wystarczy wykazać, że półprosta 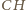 jest dwusieczną kąta
jest dwusieczną kąta 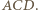
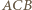 jest prosty, więc punkty
jest prosty, więc punkty 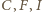 i punkt styczności okręgu wpisanego w trójkąt
i punkt styczności okręgu wpisanego w trójkąt 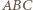 z bokiem
z bokiem 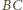 tworzą kwadrat. Stąd
tworzą kwadrat. Stąd 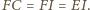
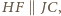 równości odcinków, twierdzenia Talesa dla
równości odcinków, twierdzenia Talesa dla 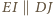 i twierdzenia o dwusiecznej, uzyskujemy
i twierdzenia o dwusiecznej, uzyskujemy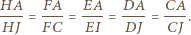
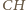 jest dwusieczną kąta
jest dwusieczną kąta 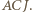
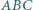 punkty
punkty 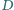 i
i 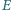 są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach
są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach 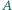 i
i 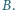 Punkt
Punkt 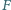 jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku
jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku 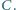 Wykaż, że punkty
Wykaż, że punkty 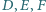 są współliniowe.
są współliniowe.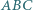 wpisany jest okrąg o promieniu
wpisany jest okrąg o promieniu 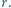 Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa
Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa 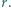

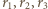 oznaczają odpowiednio promienie okręgów wpisanych w trójkąty
oznaczają odpowiednio promienie okręgów wpisanych w trójkąty 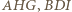 i
i 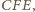 a
a 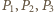 - obwody tych trójkątów. Ponadto niech
- obwody tych trójkątów. Ponadto niech 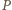 oznacza obwód trójkąta
oznacza obwód trójkąta 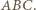
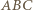 oraz punktów
oraz punktów 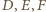 ) otrzymujemy
) otrzymujemy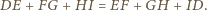
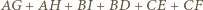
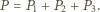
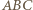 wynika, że dla
wynika, że dla 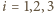 zachodzi równość
zachodzi równość