Zadanie ZM-1578
o zadaniu...
- Publikacja w Delcie: wrzesień 2018
- Publikacja elektroniczna: 1 września 2018
Rozważamy trójkąt równoboczny 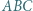 o boku
o boku 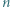 podzielony na
podzielony na 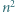 trójkątów równobocznych o boku
trójkątów równobocznych o boku 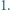 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 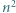 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę trójkątów równobocznych o wierzchołkach w węzłach (ale bokach niekoniecznie równoległych do boków 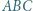 ).
).
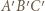 o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli
o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli 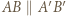 oraz punkty
oraz punkty 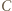 i
i 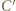 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 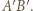
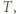 spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli
spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli 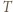 jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do
jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do 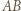 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 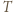 leżący najbliżej
leżący najbliżej 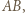 równoległą do
równoległą do 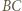 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 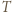 leżący najbliżej
leżący najbliżej 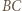 oraz równoległą do
oraz równoległą do 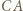 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 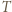 leżący najbliżej
leżący najbliżej 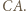
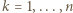 zostało w ten sposób przyporządkowanych dokładnie
zostało w ten sposób przyporządkowanych dokładnie 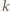 trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku
trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku 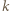 jest równa
jest równa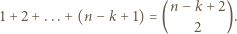
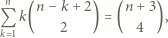
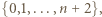 którego drugim co do wielkości elementem jest
którego drugim co do wielkości elementem jest 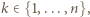 można wybrać na dokładnie
można wybrać na dokładnie 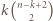 sposobów (wybierając najmniejszy element spośród
sposobów (wybierając najmniejszy element spośród 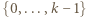 oraz dwa większe od
oraz dwa większe od 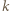 spośród
spośród 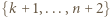 ). Sumując po wszystkich możliwych
). Sumując po wszystkich możliwych 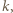 uzyskujemy liczbę sposobów wyboru
uzyskujemy liczbę sposobów wyboru 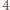 spośród
spośród 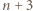 elementów.
elementów.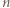 ) oraz w poprzednim (dla trójkąta o boku
) oraz w poprzednim (dla trójkąta o boku 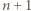 ).
).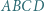 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 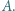 Zakładamy, że proste
Zakładamy, że proste 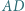 i
i 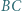 przecinają się w punkcie
przecinają się w punkcie 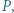 zaś proste
zaś proste 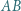 i
i 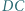 przecinają się w punkcie
przecinają się w punkcie 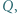 przy czym
przy czym 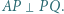 Niech
Niech 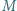 będzie środkiem przekątnej
będzie środkiem przekątnej 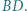 Wykazać, że
Wykazać, że 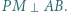
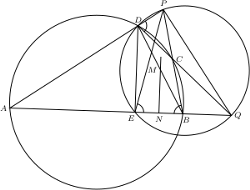
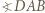 jest najmniejszym kątem czworokąta
jest najmniejszym kątem czworokąta 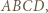 nietrudno wywnioskować, że punkt
nietrudno wywnioskować, że punkt 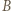 leży między
leży między 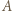 i
i 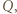 a punkt
a punkt 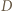 między
między 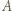 i
i 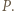 Weźmy pod uwagę okrąg o średnicy
Weźmy pod uwagę okrąg o średnicy 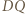 ; ów okrąg przechodzi przez punkt
; ów okrąg przechodzi przez punkt 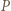 (bo
(bo 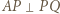 ) oraz przecina odcinek
) oraz przecina odcinek 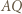 w punkcie, który nazwiemy
w punkcie, który nazwiemy 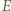 ; zatem
; zatem 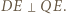
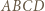 i
i 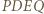 ma okrąg opisany. Wynikają stąd równości kątów
ma okrąg opisany. Wynikają stąd równości kątów 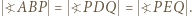 Zatem trójkąt
Zatem trójkąt 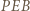 jest równoramienny.
jest równoramienny.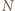 będzie środkiem odcinka
będzie środkiem odcinka 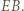 Skoro
Skoro 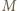 jest środkiem odcinka
jest środkiem odcinka 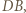 prosta
prosta 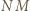 jest równoległa do prostej
jest równoległa do prostej 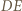 - która jest prostopadła do
- która jest prostopadła do 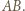 To znaczy, że prosta
To znaczy, że prosta 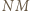 jest symetralną podstawy
jest symetralną podstawy 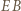 trójkąta równoramiennego
trójkąta równoramiennego 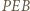 ; przechodzi więc przez punkt
; przechodzi więc przez punkt 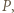 i mamy tezę
i mamy tezę 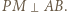
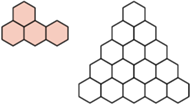
 oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei
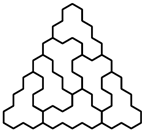
oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei 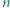 -trójkątem nazwiemy trójkątny układ tworzony przez
-trójkątem nazwiemy trójkątny układ tworzony przez 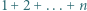 sześciokątów foremnych o boku
sześciokątów foremnych o boku 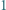 (na rysunku pokazano
(na rysunku pokazano 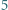 -trójkąt). Znaleźć wszystkie dodatnie liczby całkowite
-trójkąt). Znaleźć wszystkie dodatnie liczby całkowite 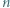 o tej własności, że z pewnej liczby płytek można ułożyć
o tej własności, że z pewnej liczby płytek można ułożyć 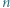 -trójkąt.
-trójkąt.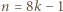 lub
lub 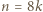 dla
dla 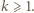
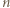 -trójkąt można ułożyć z płytek, to jest on złożony z podzielnej przez
-trójkąt można ułożyć z płytek, to jest on złożony z podzielnej przez 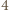 liczby sześciokątów foremnych o boku
liczby sześciokątów foremnych o boku 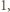 co oznacza, że liczba
co oznacza, że liczba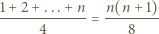
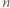 daje resztę 0 lub
daje resztę 0 lub 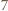 przy dzieleniu przez
przy dzieleniu przez 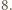
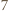 -trójkąt oraz
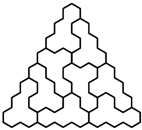
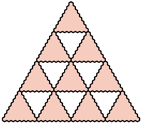
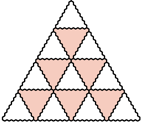
-trójkąt oraz 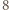 -trójkąt można ułożyć z płytek. Ponadto dla każdego
-trójkąt można ułożyć z płytek. Ponadto dla każdego 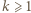 z
z 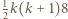 -trójkątów oraz
-trójkątów oraz 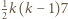 -trójkątów można ułożyć
-trójkątów można ułożyć 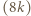 -trójkąt, a z
-trójkąt, a z 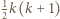
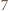 -trójkątów oraz
-trójkątów oraz 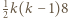 -trójkątów można ułożyć
-trójkątów można ułożyć 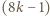 -trójkąt (rysunki 3 i 4;
-trójkąt (rysunki 3 i 4; 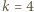 ).
).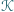 znajduje się wielokąt wypukły
znajduje się wielokąt wypukły  o polu większym od
o polu większym od 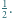 Wykazać, że wewnątrz wielokąta
Wykazać, że wewnątrz wielokąta  można wskazać odcinek o długości
można wskazać odcinek o długości  równoległy do boku kwadratu
równoległy do boku kwadratu 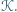
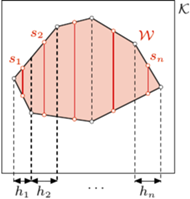
 przez wszystkie wierzchołki wielokąta
przez wszystkie wierzchołki wielokąta 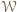 - dzielą one
- dzielą one 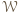 na pewną liczbę trapezów i trójkątów
na pewną liczbę trapezów i trójkątów 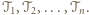 Niech
Niech 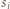 będzie odcinkiem łączącym środki tych boków wielokąta
będzie odcinkiem łączącym środki tych boków wielokąta 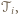 które nie są równoległe do poprowadzonych prostych, a
które nie są równoległe do poprowadzonych prostych, a 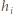 - wysokością
- wysokością 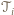 prostopadłą do
prostopadłą do 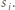 Wówczas
Wówczas![[𝒯i] = sihi](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/10x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
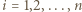 oraz
oraz![n [𝒲] = Q [𝒯 ], i 1 i](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/12x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/13x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 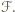 Zauważmy, że gdyby każdy z odcinków
Zauważmy, że gdyby każdy z odcinków 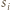 miał długość nie większą od
miał długość nie większą od 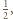 to uzyskalibyśmy nierówność
to uzyskalibyśmy nierówność![n n [𝒲] = Q sihi ⩽ 12Q hi⩽ 12, i 1 i 1](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/17x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
![1 [𝒲] > 2.](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/18x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-im-66,57,43-FF,FF,FF.gif) Wobec tego dla pewnego
Wobec tego dla pewnego 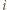 mamy
mamy 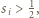 czyli
czyli 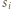 zawiera odcinek o postulowanej własności.
zawiera odcinek o postulowanej własności.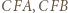 mają podstawy równe
mają podstawy równe 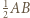 i wspólną wysokość z
i wspólną wysokość z 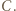
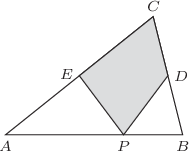
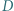 i
i 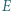 są środkami odpowiednio boków
są środkami odpowiednio boków 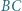 i
i 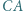 trójkąta
trójkąta 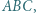 punkt
punkt 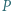 leży na boku
leży na boku 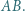 Wyznacz możliwe wartości
Wyznacz możliwe wartości ![CE] [A[PBDC].](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/8x-d6b862d2b936660f4e232be0352df6872ed9f71a-im-2C,6B,73-FF,FF,FF.gif)
![CE] [A[PBDC]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/1x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif) gdyż
gdyż ![C]=[PDB] [PD](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/2x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![[PEC]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/3x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif)
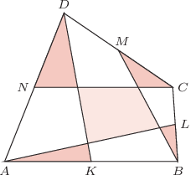
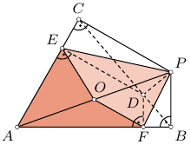
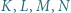 są środkami boków czworokąta wypukłego
są środkami boków czworokąta wypukłego 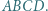 Wykaż, że suma pól ciemnych trójkątów równa jest polu jasnego czworokąta.
Wykaż, że suma pól ciemnych trójkątów równa jest polu jasnego czworokąta.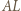 i
i 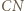 są środkowymi odpowiednio w trójkątach
są środkowymi odpowiednio w trójkątach 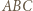 i
i 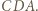 Stąd i z zadania 1 mamy
Stąd i z zadania 1 mamy ![1 ]=2[ABC][ABL] |](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/5x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) Podobnie
Podobnie ![K]+[BDM]=12[ABCD].[BD](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/6x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) Zatem
Zatem ![]=[BMDK], [ABL]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/7x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) co, po odjęciu od obu stron ich części wspólnej, kończy dowód.
co, po odjęciu od obu stron ich części wspólnej, kończy dowód.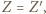 gdyż
gdyż 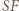 jest środkową w trójkącie
jest środkową w trójkącie 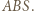 Analogicznie
Analogicznie 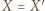 i
i 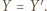 Ale także
Ale także 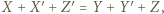 bo
bo 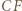 jest środkową trójkąta
jest środkową trójkąta 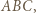 co wobec powyższego daje
co wobec powyższego daje 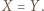 Podobnie
Podobnie 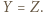
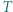 należy do wnętrza trójkąta
należy do wnętrza trójkąta 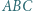 oraz
oraz 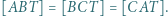 Wykaż, że
Wykaż, że 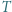 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 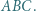
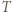 leży wewnątrz lub na brzegu trójkąta
leży wewnątrz lub na brzegu trójkąta 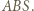 Wtedy jeśli
Wtedy jeśli 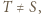 to
to 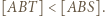 Z treści zadania wynika, że
Z treści zadania wynika, że 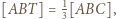 a z zadania 4 wiemy, że
a z zadania 4 wiemy, że ![|[ABS]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-5/6x-4d0410538dd904420200c91e9bf3d520281bcf04-im-66,57,43-FF,FF,FF.gif) Stąd
Stąd 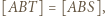 więc
więc 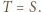
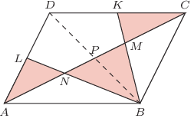
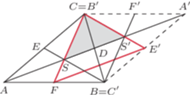
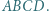 Punkty
Punkty 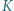 i
i 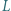 są środkami boków
są środkami boków 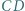 i
i 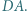 Proste
Proste 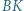 i
i 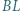 przecinają przekątną
przecinają przekątną 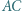 odpowiednio w punktach
odpowiednio w punktach 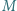 i
i 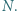 Wykaż, że
Wykaż, że ![1 ]+[BMN]+[CKM]=3[ABCD] |[ALN](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/11x-a985b0af3fbf2b8f27676b5a2afc831fe04a782f-im-2C,6B,73-FF,FF,FF.gif) oraz że
oraz że 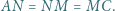
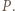 Odcinki
Odcinki 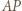 i
i 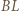 oraz
oraz 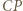 i
i 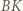 są zatem środkowymi odpowiednio w trójkątach
są zatem środkowymi odpowiednio w trójkątach 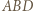 i
i 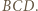 Trójkąty te mają pola równe
Trójkąty te mają pola równe ![1[ABCD] 2](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/8x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd
i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd ![12111 ]+[BMN]+[CKM]=(6+6+6)⋅2[ABCD]=3[ABCD] [ALN .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/9x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) Ponadto
Ponadto 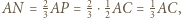 podobnie
podobnie 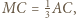 więc też
więc też 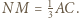
 o
o 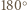 wokół punktu
wokół punktu  Boki trójkąta
Boki trójkąta  mają długości
mają długości 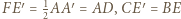 oraz
oraz 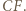
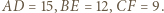 Obróćmy trójkąt
Obróćmy trójkąt 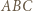 o
o 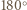 wokół punktu
wokół punktu 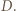 Trójkąt
Trójkąt 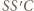 ma wówczas boki o długościach
ma wówczas boki o długościach 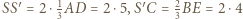 oraz
oraz 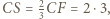 jest więc prostokątny. Stąd jego pole równe jest
jest więc prostokątny. Stąd jego pole równe jest 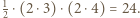 Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest
Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest 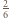 pola trójkąta
pola trójkąta 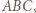 zatem
zatem ![|[ABC] .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-8/11x-8282951b1e1d6cfb55ae221251f78463d5dae986-im-66,57,43-FF,FF,FF.gif)
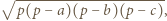
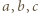 to boki,
to boki, 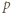 - połowa obwodu.
- połowa obwodu.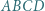 podstawa
podstawa 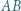 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 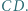 Punkt
Punkt 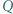 jest środkiem przekątnej
jest środkiem przekątnej 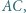 a prosta
a prosta 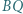 przecina bok
przecina bok 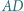 w punkcie
w punkcie 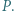 Wyznacz
Wyznacz ![[PQCD]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-9/9x-59beed1787f722ef146fe03a4f1f01fb55efe3fb-im-2C,6B,73-FF,FF,FF.gif)
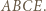
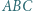 wyznacz zbiór takich punktów
wyznacz zbiór takich punktów 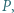 że miary kątów
że miary kątów 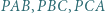 tworzą w tej właśnie kolejności ciąg arytmetyczny.
tworzą w tej właśnie kolejności ciąg arytmetyczny.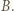
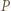 tej wysokości mamy
tej wysokości mamy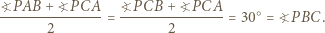
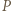 wnętrza trójkąta równobocznego
wnętrza trójkąta równobocznego 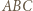 jest taki, że
jest taki, że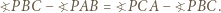
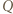 obraz punktu
obraz punktu 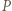 w obrocie wokół
w obrocie wokół 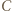 przeprowadzającym
przeprowadzającym 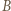 na
na 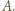 Wówczas trójkąt
Wówczas trójkąt 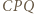 jest równoboczny.
jest równoboczny.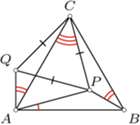
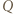 obraz punktu
obraz punktu 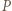 w obrocie wokół
w obrocie wokół 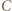 przeprowadzającym
przeprowadzającym 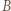 na
na 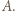 Wówczas trójkąt
Wówczas trójkąt 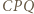 jest równoboczny.
jest równoboczny.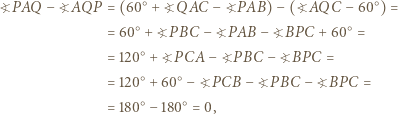
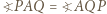 i
i 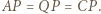 To oznacza, że punkt
To oznacza, że punkt 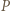 leży na symetralnej odcinka
leży na symetralnej odcinka 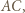 czyli na wysokości trójkąta
czyli na wysokości trójkąta 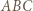 opuszczonej z
opuszczonej z 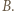
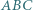 (nie prostokątny) jest wpisany w okrąg o średnicy
(nie prostokątny) jest wpisany w okrąg o średnicy 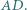 Punkt
Punkt 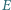 jest symetryczny do
jest symetryczny do 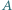 względem środka boku
względem środka boku 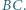 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 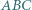 i
i 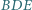 mają równe promienie.
mają równe promienie.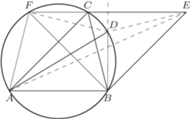
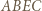 jest równoległobokiem. Niech prosta
jest równoległobokiem. Niech prosta 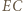 przecina okrąg, opisany na trójkącie
przecina okrąg, opisany na trójkącie 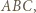 w punktach
w punktach 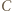 i
i 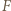 (gdy jest styczna, przyjmujemy
(gdy jest styczna, przyjmujemy 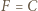 ). Powstaje trapez równoramienny
). Powstaje trapez równoramienny 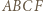 lub
lub 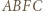 (gdy
(gdy 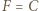 - trójkąt równoramienny). W każdym przypadku
- trójkąt równoramienny). W każdym przypadku 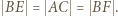
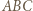 z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą
z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą 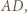 na której oparty jest kąt prosty
na której oparty jest kąt prosty 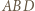 ; a ponieważ
; a ponieważ 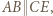 zatem
zatem 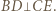 To znaczy, że w trójkącie równoramiennym
To znaczy, że w trójkącie równoramiennym 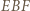 prosta
prosta 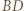 jest symetralną boku
jest symetralną boku 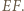 W konsekwencji trójkąt
W konsekwencji trójkąt 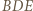 jest względem niej symetryczny do trójkąta
jest względem niej symetryczny do trójkąta  Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie
Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie 
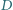 leży na boku
leży na boku 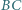 trójkąta ostrokątnego
trójkąta ostrokątnego 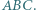 Punkty
Punkty 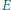 i
i 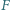 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 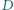 odpowiednio na boki
odpowiednio na boki 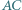 i
i 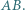 Punkt
Punkt 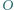 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie  Udowodnić, że pole czworokąta
Udowodnić, że pole czworokąta  jest równe połowie pola trójkąta
jest równe połowie pola trójkąta 
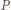 punkt symetryczny do
punkt symetryczny do 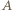 względem
względem 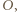 czyli taki punkt, że odcinek
czyli taki punkt, że odcinek 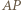 jest średnicą okręgu opisanego na trójkącie
jest średnicą okręgu opisanego na trójkącie 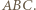 Wówczas
Wówczas 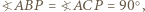 wobec czego
wobec czego 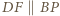 oraz
oraz 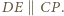 Stąd
Stąd ![F]=[PDF] |[BD](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/9x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![[CDE]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/10x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) a zatem
a zatem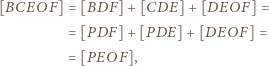
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/12x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 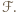 Ponieważ punkt
Ponieważ punkt 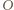 jest środkiem odcinka
jest środkiem odcinka 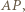 więc
więc ![F]=[AOF] [PO](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/16x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![E]=[AOE] [PO](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/17x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) i w konsekwencji
i w konsekwencji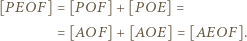
![EOF], |[BCEOF]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/19x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) co jest równoznaczne z tezą zadania.
co jest równoznaczne z tezą zadania.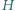 jest ortocentrum trójkąta
jest ortocentrum trójkąta 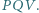
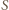 zamienia punkty
zamienia punkty 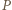 i
i 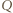 oraz punkty
oraz punkty 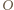 i
i 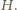 Symetralna odcinka
Symetralna odcinka 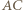 jest do niego prostopadła, przechodzi przez jego środek
jest do niego prostopadła, przechodzi przez jego środek 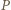 i przez
i przez 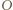 - środek okręgu, w którym
- środek okręgu, w którym 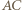 jest cięciwą. Jej obrazem w symetrii względem
jest cięciwą. Jej obrazem w symetrii względem 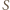 jest więc prosta prostopadła do
jest więc prosta prostopadła do 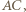 przechodząca przez
przechodząca przez 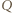 (czyli wysokość trójkąta
(czyli wysokość trójkąta 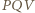 ) i przez
) i przez 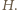 Analogicznie wysokość trójkąta
Analogicznie wysokość trójkąta 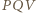 z wierzchołka
z wierzchołka 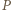 też przechodzi przez
też przechodzi przez 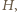 co kończy dowód.
co kończy dowód.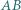 i
i 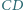 przecinają się w punkcie
przecinają się w punkcie 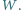 Wykaż, że
Wykaż, że 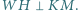
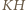 i
i 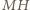 są wysokościami trójkąta
są wysokościami trójkąta 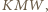 więc
więc 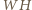 też jest.
też jest.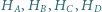 będą odpowiednio ortocentrami trójkątów
będą odpowiednio ortocentrami trójkątów 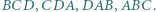 Wykaż, że odcinki
Wykaż, że odcinki 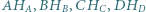 mają wspólny punkt.
mają wspólny punkt.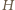 jest ich wspólnym środkiem.
jest ich wspólnym środkiem.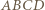 oraz
oraz 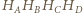 są przystające, co daje inne rozwiązanie zadania 4 z
są przystające, co daje inne rozwiązanie zadania 4 z 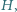 środek ciężkości
środek ciężkości 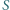 i środek okręgu opisanego
i środek okręgu opisanego  leżą na jednej prostej (prostej Eulera), w tej kolejności i
leżą na jednej prostej (prostej Eulera), w tej kolejności i