Klub 44M - zadania III 2017»Zadanie 737
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2017
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (67 KB)
Pięciokąt 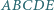 jest wpisany w okrąg
jest wpisany w okrąg 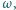 przy czym proste
przy czym proste 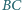 i
i 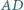 przecinają się w takim punkcie
przecinają się w takim punkcie 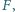 że prosta
że prosta 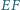 jest styczna do
jest styczna do 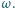 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 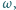 równoległa do
równoległa do 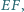 przecina proste
przecina proste 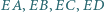 odpowiednio w punktach
odpowiednio w punktach 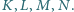 Udowodnić, że odcinki
Udowodnić, że odcinki 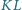 i
i 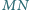 mają jednakową długość.
mają jednakową długość.

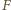 prostą różną od
prostą różną od 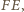 styczną do okręgu
styczną do okręgu 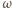 w punkcie
w punkcie 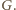 Prosta przechodząca przez punkty
Prosta przechodząca przez punkty 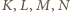 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 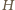 i przecina prostą
i przecina prostą 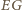 w punkcie
w punkcie 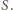 Pokażemy, że
Pokażemy, że 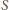 jest środkiem odcinka
jest środkiem odcinka 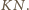 Ponieważ
Ponieważ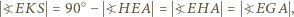
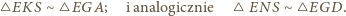
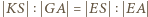 oraz
oraz 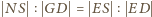 ; a z nich -
; a z nich -
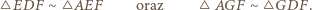
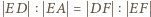 oraz
oraz 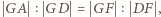 z których wynika, że prawa strona wzoru (1) jest równa
z których wynika, że prawa strona wzoru (1) jest równa 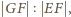 czyli 1.
czyli 1.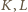 leżą po jednej stronie punktu
leżą po jednej stronie punktu 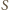 ; punkty
; punkty 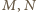 po drugiej. Uzyskana równość
po drugiej. Uzyskana równość 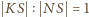 oznacza, że
oznacza, że 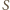 jest środkiem odcinka
jest środkiem odcinka 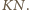 Przez analogię, ten sam punkt
Przez analogię, ten sam punkt 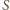 jest też środkiem odcinka
jest też środkiem odcinka 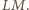 Stąd wniosek, że odcinki
Stąd wniosek, że odcinki 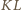 i
i 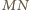 są przystające.
są przystające.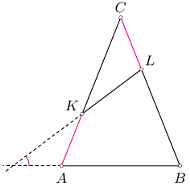
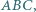 w którym
w którym 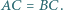 Na odcinkach
Na odcinkach 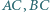 znajdują się odpowiednio takie punkty
znajdują się odpowiednio takie punkty 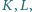 że
że 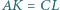 oraz
oraz 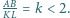 Wyznaczyć, w zależności od
Wyznaczyć, w zależności od 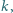 miarę kąta między prostymi
miarę kąta między prostymi 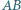 i
i 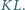
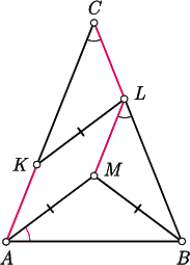
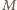 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt 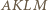 jest równoległobokiem. Wówczas
jest równoległobokiem. Wówczas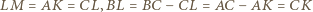
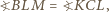
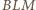 oraz
oraz 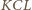 są przystające (cecha bok-kąt-bok). Zatem
są przystające (cecha bok-kąt-bok). Zatem 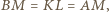 czyli trójkąt
czyli trójkąt 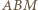 jest równoramienny, więc
jest równoramienny, więc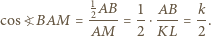
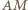 i
i 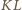 są równoległe, więc
są równoległe, więc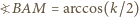
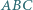 bok
bok 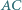 jest dłuższy niż
jest dłuższy niż 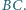 Punkt
Punkt 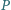 leży na dwusiecznej
leży na dwusiecznej 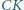 kąta
kąta 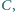 zaś punkt
zaś punkt 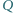 leży na środkowej
leży na środkowej 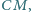 połowiącej bok
połowiącej bok 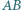 ; przy tym
; przy tym 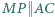 oraz
oraz 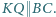 Wykazać, że odcinek
Wykazać, że odcinek 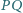 jest prostopadły do
jest prostopadły do 
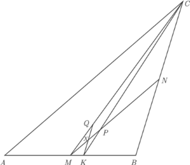
 punkt przecięcia przekątnych czworokąta
punkt przecięcia przekątnych czworokąta 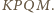 Prosta
Prosta 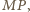 równoległa do
równoległa do 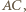 przecina bok
przecina bok 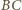 w punkcie
w punkcie 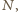 będącym środkiem tego boku. Skoro ów bok jest równoległy do
będącym środkiem tego boku. Skoro ów bok jest równoległy do 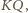 zatem punkt
zatem punkt 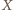 (leżący na prostej
(leżący na prostej 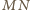 ) jest środkiem odcinka
) jest środkiem odcinka 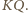
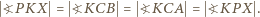
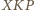 jest więc równoramienny:
jest więc równoramienny: 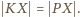 Punkt
Punkt 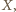 jako środek odcinka
jako środek odcinka 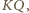 jest w takim razie środkiem okręgu opisanego na trójkącie
jest w takim razie środkiem okręgu opisanego na trójkącie 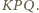 Wynika stąd, że kąt
Wynika stąd, że kąt 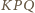 jest prosty - a to teza zadania.
jest prosty - a to teza zadania.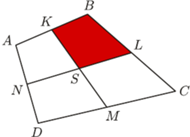
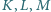 i
i 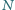 są odpowiednio środkami boków
są odpowiednio środkami boków 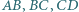 i
i 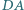 czworokąta wypukłego
czworokąta wypukłego 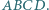 Odcinki
Odcinki 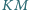 i
i 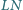 przecinają się w punkcie
przecinają się w punkcie 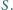 Znaleźć kres dolny i górny pola czworokąta
Znaleźć kres dolny i górny pola czworokąta 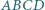 przy założeniu, że pole czworokąta
przy założeniu, że pole czworokąta 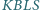 jest równe
jest równe 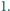
![|[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/1x-9dbfe84ebf61bac61555ddb19dc430d0032fb9e1-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 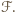
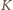 i
i 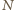 są środkami odcinków
są środkami odcinków 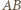 i
i 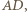 to
to 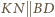 oraz
oraz 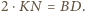 Podobnie otrzymujemy
Podobnie otrzymujemy 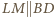 oraz
oraz 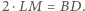 W takim razie czworokąt
W takim razie czworokąt 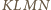 ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku
ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku 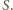 Ponadto trójkąt
Ponadto trójkąt 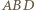 jest obrazem trójkąta
jest obrazem trójkąta 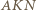 w jednokładności o środku
w jednokładności o środku 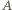 i skali
i skali 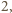 więc
więc ![]=4⋅[A].[AKBND](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/15x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) Z analogicznych rozważań dla trójkątów
Z analogicznych rozważań dla trójkątów 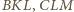 i
i 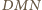 otrzymujemy
otrzymujemy![]+4⋅[BKL]+4⋅[C]+4⋅[DMN]=[ADB]+[BAC]+[CBD]+[DCA]=2⋅[ABCD].4L⋅[MAKN](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/18x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![N]=8⋅[KLS]. [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/19x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![4 ⋅[BKL] = [BAC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/20x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![-1 [KBLS] = [KBL] + [KLS] ⩽ 4 [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/21x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![1- [KBLS] ⩾ [KLS] = 8[ABCD].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/22x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![8-⩽ [ABCD] 3](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/23x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
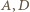 i
i 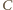 są współliniowe (wówczas
są współliniowe (wówczas ![[ABC] |](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/26x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ), a maksimum - gdy wierzchołki
), a maksimum - gdy wierzchołki 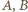 i
i 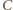 są współliniowe (wówczas
są współliniowe (wówczas ![|[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/29x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ).
).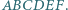 Każda z przekątnych
Każda z przekątnych 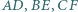 dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.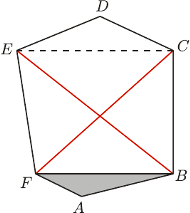
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/1x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 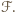 Skoro
Skoro ![1 |[BACF] = 2[BACDEF] = [ABEF],](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/3x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) to
to ![|[FBC] = [FBE].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/4x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) Trójkąty te mają wspólną podstawę
Trójkąty te mają wspólną podstawę 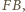 zatem mają też równe wysokości na nią. Ponieważ punkty
zatem mają też równe wysokości na nią. Ponieważ punkty 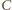 i
i 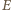 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 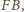 wynika stąd, że
wynika stąd, że 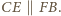 Analogicznie
Analogicznie 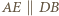 oraz
oraz 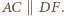
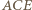 i
i 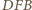 spełniają założenia twierdzenia
spełniają założenia twierdzenia 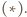 Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków
Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków 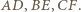
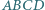 oraz punkt
oraz punkt 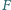 leżący na odcinku
leżący na odcinku 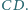 Punkty
Punkty 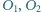 i
i 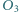 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 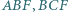 i
i 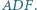 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 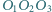 leży na prostej
leży na prostej 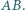
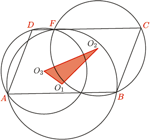
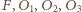 leżą na jednym okręgu. Istotnie,
leżą na jednym okręgu. Istotnie,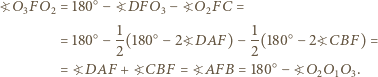
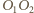 i
i 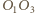 są prostopadłe odpowiednio do
są prostopadłe odpowiednio do 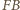 i
i 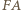 ). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu
). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu 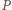 względem boków trójkąta
względem boków trójkąta 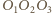 leżą na prostej
leżą na prostej 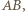 jednakże jest to oczywiste, gdyż proste
jednakże jest to oczywiste, gdyż proste 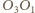 oraz
oraz 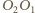 są symetralnymi odcinków odpowiednio
są symetralnymi odcinków odpowiednio 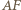 i
i 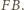
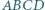 opisanym na okręgu prosta
opisanym na okręgu prosta 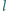 przechodząca przez wierzchołek
przechodząca przez wierzchołek 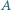 przecina bok
przecina bok 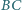 w punkcie
w punkcie 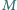 oraz półprostą
oraz półprostą 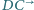 w punkcie
w punkcie 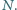 Punkty
Punkty 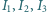 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 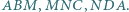 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 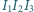 leży na prostej
leży na prostej 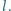
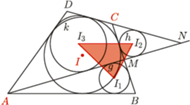
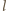 przecina półprostą
przecina półprostą 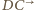 w punkcie
w punkcie 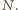 Trójki punktów
Trójki punktów 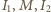 oraz
oraz 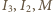 są, oczywiście, współliniowe. Oznaczmy przez
są, oczywiście, współliniowe. Oznaczmy przez 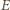 przecięcie prostych
przecięcie prostych 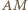 i drugiej stycznej poprowadzonej z punktu
i drugiej stycznej poprowadzonej z punktu 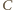 do okręgu o środku w punkcie
do okręgu o środku w punkcie 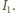 Łatwo zauważyć, że
Łatwo zauważyć, że 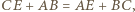 więc
więc 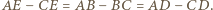 Oznacza to, że półprosta
Oznacza to, że półprosta 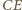 jest również styczna do okręgu o środku w punkcie
jest również styczna do okręgu o środku w punkcie 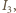 stąd punkty
stąd punkty 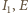 i
i 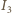 są współliniowe. Wobec tego
są współliniowe. Wobec tego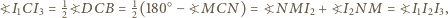
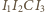 można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu
można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu 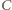 w symetrii względem prostych
w symetrii względem prostych 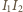 oraz
oraz 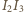 leżą na prostej
leżą na prostej 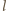 i zastosować twierdzenie Steinera.
i zastosować twierdzenie Steinera.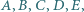 takie, że czworokąt
takie, że czworokąt 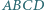 jest równoległobokiem, a czworokąt
jest równoległobokiem, a czworokąt 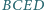 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 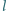 przechodząca przez
przechodząca przez 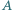 przecina wnętrze odcinka
przecina wnętrze odcinka 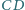 w punkcie
w punkcie 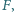 a prostą
a prostą 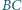 w punkcie
w punkcie 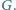 Przypuśćmy, że
Przypuśćmy, że 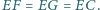 Wykazać, że
Wykazać, że 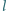 jest dwusieczną kąta
jest dwusieczną kąta 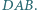
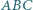 wpisany w okrąg
wpisany w okrąg 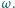 Punkt
Punkt 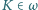 i punkt
i punkt 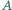 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 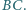 Punkty
Punkty 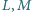 są odbiciami punktu
są odbiciami punktu 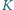 względem
względem 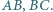 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 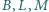 przecina
przecina 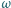 po raz drugi w punkcie
po raz drugi w punkcie 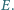 Punkt
Punkt 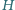 jest ortocentrum trójkąta
jest ortocentrum trójkąta 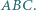 Wykazać, że proste
Wykazać, że proste 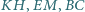 mają punkt wspólny.
mają punkt wspólny.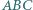 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków 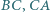 i
i 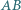 w punktach odpowiednio
w punktach odpowiednio 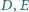 i
i 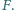 Punkt
Punkt 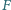 jest punktem Feuerbacha trójkąta
jest punktem Feuerbacha trójkąta 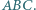 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 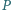 względem trójkąta
względem trójkąta 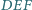 jest równoległa do prostej
jest równoległa do prostej 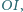 która łączy środki
która łączy środki 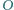 i
i 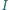 - okręgów opisanego i wpisanego trójkąta
- okręgów opisanego i wpisanego trójkąta 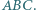
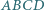 o obwodzie
o obwodzie 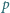 został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie
został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie 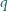 . Wykazać, że pole
. Wykazać, że pole 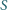 czworokąta
czworokąta 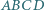 jest mniejsze niż
jest mniejsze niż 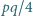 .
.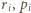 i
i 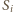 oznaczają dla
oznaczają dla 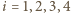 odpowiednio promienie okręgów wpisanych, obwody i pola powstałych czterech trójkątów. Wiemy, że wówczas dla każdego
odpowiednio promienie okręgów wpisanych, obwody i pola powstałych czterech trójkątów. Wiemy, że wówczas dla każdego 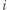 zachodzi równość
zachodzi równość 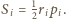 W takim razie
W takim razie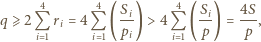
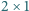 ułożono szachownicę
ułożono szachownicę 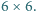 Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.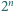 dowolnego spośród
dowolnego spośród 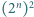 tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami
tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami 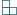 , zbudowanymi z trzech kwadratów jednostkowych.
, zbudowanymi z trzech kwadratów jednostkowych.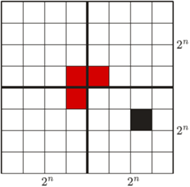
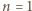 teza jest prawdziwa: rozważana figura jest pojedynczym klockiem. Załóżmy, że teza zachodzi dla pewnego
teza jest prawdziwa: rozważana figura jest pojedynczym klockiem. Załóżmy, że teza zachodzi dla pewnego 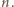 Niech
Niech 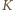 będzie kwadratem o krawędzi
będzie kwadratem o krawędzi 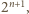 z którego usuwamy jedno pole. Podzielmy
z którego usuwamy jedno pole. Podzielmy 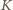 na cztery przystające mniejsze kwadraty o krawędzi
na cztery przystające mniejsze kwadraty o krawędzi 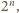 jeden z nich zawiera usunięte pole. Umieśćmy pojedynczy klocek na środku kwadratu
jeden z nich zawiera usunięte pole. Umieśćmy pojedynczy klocek na środku kwadratu 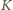 w sposób przedstawiony na rysunku Wówczas na mocy założenia indukcyjnego każdy z czterech mniejszych kwadratów bez jednego pola da się szczelnie wypełnić klockami, co kończy dowód.
w sposób przedstawiony na rysunku Wówczas na mocy założenia indukcyjnego każdy z czterech mniejszych kwadratów bez jednego pola da się szczelnie wypełnić klockami, co kończy dowód.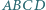 kąty przy wierzchołkach
kąty przy wierzchołkach 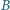 i
i 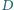 są proste. Przekątne przecinają się w punkcie
są proste. Przekątne przecinają się w punkcie 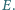 Prosta prostopadła do
Prosta prostopadła do 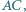 przechodząca przez punkt
przechodząca przez punkt 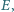 przecina proste
przecina proste 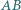 i
i 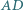 w punktach
w punktach 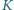 i
i 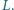 Wykazać, że punkty
Wykazać, że punkty 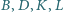 leżą na jednym okręgu.
leżą na jednym okręgu.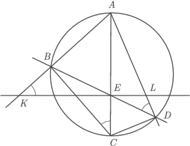
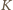 i
i 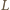 pokrywają się z
pokrywają się z 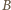 i
i 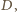 i nie ma czego dowodzić. Przyjmijmy dalej, nie tracąc ogólności, że kąt
i nie ma czego dowodzić. Przyjmijmy dalej, nie tracąc ogólności, że kąt 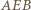 jest ostry (wtedy punkt
jest ostry (wtedy punkt 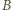 leży między
leży między 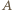 i
i 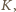 zaś
zaś 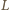 leży między
leży między 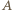 i
i 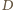 ). Czworokąt
). Czworokąt 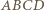 ma okrąg opisany (o średnicy
ma okrąg opisany (o średnicy 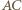 ). Stąd oraz z zależności w trójkątach prostokątnych
). Stąd oraz z zależności w trójkątach prostokątnych 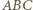 i
i 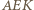 dostajemy ciąg równości
dostajemy ciąg równości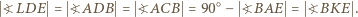
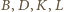 na wspólnym okręgu.
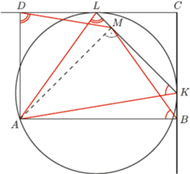
na wspólnym okręgu.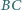 i
i 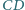 prostokąta
prostokąta 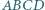 są styczne odpowiednio w punktach
są styczne odpowiednio w punktach 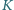 i
i 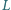 do okręgu przechodzącego przez
do okręgu przechodzącego przez 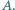 Na odcinku
Na odcinku 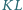 leży taki punkt
leży taki punkt 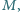 że proste
że proste 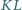 i
i 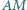 są prostopadłe. Obliczyć pole prostokąta
są prostopadłe. Obliczyć pole prostokąta 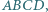 wiedząc, że odcinek
wiedząc, że odcinek 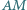 ma długość
ma długość 
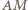 jest prostopadła do
jest prostopadła do 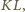 więc jest nachylona do boków prostokąta pod kątem
więc jest nachylona do boków prostokąta pod kątem 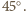 Ponadto kąt środkowy oparty na cięciwie
Ponadto kąt środkowy oparty na cięciwie 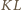 jest prosty, a stąd
jest prosty, a stąd 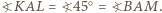
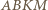 jest opisany na okręgu o średnicy
jest opisany na okręgu o średnicy 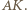 W takim razie kąty
W takim razie kąty 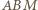 i
i 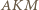 są równe.
są równe.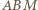 i
i 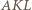 są podobne. Analogicznie trójkąty
są podobne. Analogicznie trójkąty 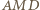 i
i 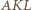 są podobne. W takim razie mamy podobieństwo trójkątów
są podobne. W takim razie mamy podobieństwo trójkątów 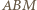 i
i 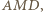 a stąd
a stąd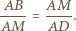
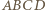 jest równe
jest równe 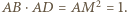
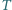 rozcięto wzdłuż odcinka na dwa trójkąty
rozcięto wzdłuż odcinka na dwa trójkąty 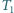 i
i 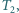 a trójkąt
a trójkąt 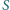 - na trójkąty
- na trójkąty 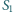 i
i 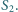 Okazało się, że trójkąt
Okazało się, że trójkąt 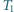 jest przystający do trójkąta
jest przystający do trójkąta 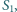 a trójkąt
a trójkąt 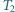 jest przystający do trójkąta
jest przystający do trójkąta 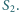 Czy wynika z tego, że trójkąty
Czy wynika z tego, że trójkąty 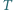 i
i 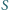 są przystające?
są przystające?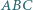 i
i 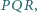 przy czym
przy czym 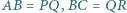 oraz
oraz 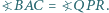 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?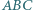 i
i 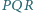 mają równe pola oraz
mają równe pola oraz 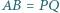 i
i 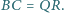 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?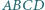 i
i 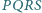 mają równe pola oraz
mają równe pola oraz 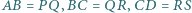 i
i 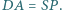 Czy wynika z tego, że czworokąty te są przystające?
Czy wynika z tego, że czworokąty te są przystające?