Ciąg Fibonacciego»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Ciąg Fibonacciego
- Publikacja w Delcie: maj 2012
- Publikacja elektroniczna: 28-04-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (90 KB)
Na ile różnych sposobów można ułożyć chodnik o długości
 i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
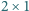 oraz
oraz
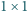 ?
?
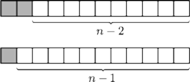
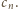 Dla
Dla
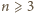 na początku
chodnika możemy położyć płytę
na początku
chodnika możemy położyć płytę
 a następnie na
a następnie na
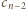 sposobów ułożyć resztę (chodnik o długości
sposobów ułożyć resztę (chodnik o długości
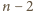 );
możemy też zacząć od płyty
);
możemy też zacząć od płyty
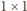 i wtedy na
i wtedy na
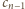 sposobów
ułożyć resztę. Stąd
sposobów
ułożyć resztę. Stąd
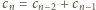 dla
dla
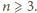 Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
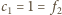 oraz
oraz
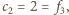 uzyskujemy więc wniosek, że
uzyskujemy więc wniosek, że
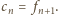
 punkt
punkt
 jest środkiem okręgu wpisanego.
Prosta
jest środkiem okręgu wpisanego.
Prosta
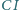 przecina bok
przecina bok
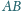 w punkcie
w punkcie
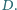 Prowadzimy
przez punkt
Prowadzimy
przez punkt
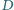 dowolną prostą, przecinającą okrąg opisany na
trójkącie
dowolną prostą, przecinającą okrąg opisany na
trójkącie
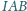 w punktach
w punktach
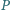 i
i
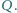 Wykazać, że prosta
Wykazać, że prosta
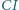 jest dwusieczną kąta
jest dwusieczną kąta
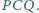

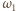 i
i
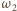 będą (odpowiednio) okręgami opisanymi
na trójkątach
będą (odpowiednio) okręgami opisanymi
na trójkątach
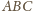 i
i
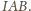 Dwusieczna
Dwusieczna
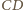 kąta
kąta
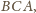 a raczej jej przedłużenie, przecina okrąg
a raczej jej przedłużenie, przecina okrąg
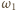 w środku
łuku
w środku
łuku
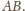 Oznaczmy ten punkt przez
Oznaczmy ten punkt przez
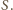 Zachodzi równość
Zachodzi równość
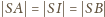 (znana, a przy tym łatwa do wykazania). Punkt
(znana, a przy tym łatwa do wykazania). Punkt
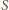 jest więc środkiem okręgu
jest więc środkiem okręgu
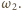 Zatem
Zatem
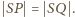
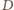 przecinają się cięciwy
przecinają się cięciwy
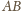 i
i
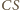 okręgu
okręgu
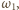 a także cięciwy
a także cięciwy
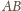 i
i
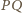 okręgu
okręgu
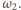 Tak
więc
Tak
więc
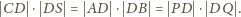
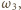 przechodzący przez punkty
przechodzący przez punkty
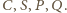 Jego cięciwy
Jego cięciwy
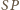 i
i
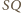 mają jednakową długość, więc wyznaczają przystające
łuki
mają jednakową długość, więc wyznaczają przystające
łuki
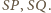 Oparte na nich kąty
Oparte na nich kąty
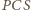 i
i
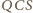 (wpisane
w okrąg
(wpisane
w okrąg
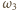 ) są równe – a to jest teza zadania.
) są równe – a to jest teza zadania.

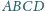 jest styczny do boków
jest styczny do boków
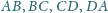 odpowiednio w punktach
odpowiednio w punktach
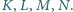 Udowodnij,
że proste
Udowodnij,
że proste
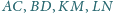 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
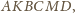 proste
proste
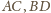 i
i
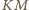 przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
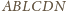 wynika, że przez punkt przecięcia prostych
wynika, że przez punkt przecięcia prostych
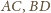 przechodzi także prosta
przechodzi także prosta
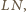 co kończy dowód.
co kończy dowód.
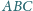 jest styczny do boków
jest styczny do boków
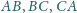 odpowiednio w punktach
odpowiednio w punktach
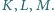 Wykaż, że
proste
Wykaż, że
proste
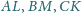 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
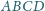 jest opisany na okręgu o środku
jest opisany na okręgu o środku
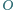 i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
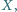 przy czym
przy czym
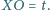 Wyznacz stosunek
Wyznacz stosunek
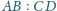 długości podstaw tego
trapezu, jeśli
długości podstaw tego
trapezu, jeśli
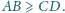
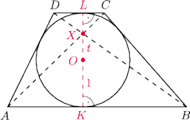
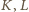 odpowiednio punkty styczności podstaw
odpowiednio punkty styczności podstaw
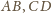 z okręgiem. Wtedy
z okręgiem. Wtedy
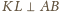 oraz
oraz
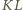 przechodzi
przez punkt
przechodzi
przez punkt
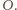 Z twierdzenia Brianchona dla czworokąta,
Z twierdzenia Brianchona dla czworokąta,
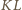 przechodzi też przez punkt
przechodzi też przez punkt
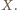 Trójkąty
Trójkąty
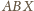 i
i
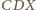 są podobne, więc
są podobne, więc
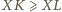 oraz
oraz
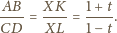
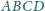 jest styczny do boku
jest styczny do boku
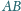 w punkcie
w punkcie
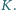 Styczna do tego okręgu przecina boki
Styczna do tego okręgu przecina boki
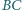 i
i
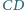 odpowiednio
w punktach
odpowiednio
w punktach
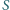 i
i
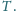 Wykaż, że
Wykaż, że

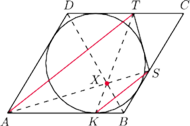
 proste
proste
 przecinają się w jednym punkcie
przecinają się w jednym punkcie
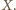 Z twierdzenia
Talesa ponieważ
Z twierdzenia
Talesa ponieważ
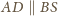 oraz
oraz
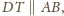 więc
więc
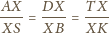
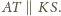
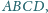 w którym zachodzi równość
w którym zachodzi równość

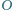 jest środkiem okręgu opisanego na trójkacie
jest środkiem okręgu opisanego na trójkacie
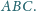 Wykaż, że punkt
Wykaż, że punkt
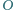 jest jednakowo odległy od prostych
jest jednakowo odległy od prostych
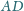 i
i
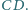
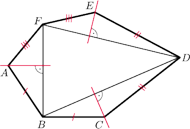
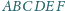 jest wypukły oraz
jest wypukły oraz
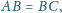
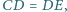
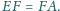 Wykaż, że proste zawierające
wysokości trójkątów
Wykaż, że proste zawierające
wysokości trójkątów
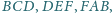 poprowadzone odpowiednio
z wierzchołków
poprowadzone odpowiednio
z wierzchołków
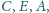 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
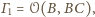
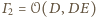 oraz
oraz
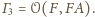 Punkt
Punkt
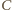 należy do
należy do
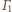 i
i
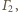 więc osią potęgową
tych okręgów jest rozważana w zadaniu prosta przechodząca przez
więc osią potęgową
tych okręgów jest rozważana w zadaniu prosta przechodząca przez
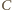 i prostopadła do prostej
i prostopadła do prostej
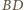 łączącej ich środki. Pozostałe
rozważane proste są osiami potęgowymi okręgów
łączącej ich środki. Pozostałe
rozważane proste są osiami potęgowymi okręgów
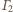 i
i
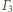 oraz
oraz
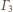 i
i
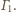 Środki
Środki
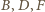 okręgów nie są współliniowe,
więc osie potęgowe przecinają się w jednym punkcie.
okręgów nie są współliniowe,
więc osie potęgowe przecinają się w jednym punkcie.
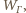 zawierającej okrąg
zawierającej okrąg
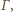 niech należą punkty,
których potęga względem
niech należą punkty,
których potęga względem
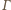 jest mniejsza niż względem innych
okręgów. Granice między częściami wyznaczają wtedy osie potęgowe
(dlaczego?)...
jest mniejsza niż względem innych
okręgów. Granice między częściami wyznaczają wtedy osie potęgowe
(dlaczego?)...
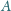 i
i
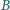 . Dany jest też kąt
skierowany
. Dany jest też kąt
skierowany
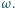 Przez
Przez
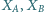 oznaczamy obraz punktu
oznaczamy obraz punktu
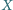 przy obrocie o kąt
przy obrocie o kąt
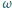 względem punktu
względem punktu
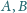 , odpowiednio.
Znaleźć wszystkie punkty
, odpowiednio.
Znaleźć wszystkie punkty
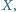 dla których trójkąt
dla których trójkąt
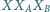 jest równoboczny.
jest równoboczny.
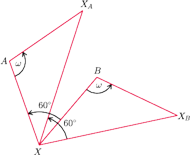
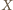 jest taki, że trójkąt
jest taki, że trójkąt
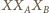 jest
równoboczny. Wówczas trójkąty
jest
równoboczny. Wówczas trójkąty
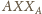 i
i
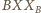 są przystające,
gdyż są podobne i
są przystające,
gdyż są podobne i
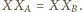 Ponieważ obrazem odcinka
Ponieważ obrazem odcinka
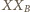 przy obrocie o kąt
przy obrocie o kąt
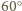 (skierowany zgodnie z kątem
(skierowany zgodnie z kątem
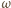 ) względem punktu
) względem punktu
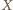 jest odcinek
jest odcinek
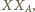 więc obrazem
trójkąta
więc obrazem
trójkąta
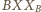 jest trójkąt
jest trójkąt
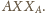 Zatem kąt
Zatem kąt
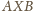 ma
miarę
ma
miarę
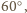 a ponadto
a ponadto
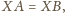 więc trójkąt
więc trójkąt
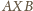 jest
równoboczny.
jest
równoboczny. 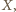 dla których trójkąt
dla których trójkąt
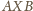 jest równoboczny.
Łatwo sprawdzić, że dla nich trójkąt
jest równoboczny.
Łatwo sprawdzić, że dla nich trójkąt
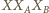 jest też równoboczny.
Zatem są to wszystkie szukane punkty.
jest też równoboczny.
Zatem są to wszystkie szukane punkty.
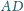 i
i
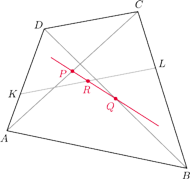
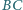 czworokąta wypukłego
czworokąta wypukłego
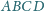 wybrano
takie punkty
wybrano
takie punkty
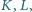 że
że
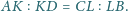 Wykaż, że środki
Wykaż, że środki
 odcinków
odcinków
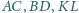 są współliniowe.
są współliniowe.
 i
i
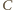 masy
masy
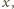 a w
a w
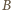 i
i
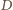 masy
masy
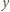 takie, by
takie, by
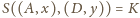 (da się takie masy
dobrać). Wtedy
(da się takie masy
dobrać). Wtedy
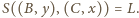 Wobec tego
Wobec tego
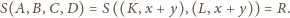
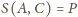 oraz
oraz
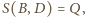 więc
więc
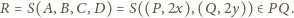
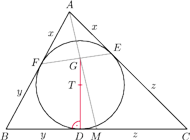
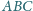 jest styczny do boków
jest styczny do boków
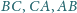 odpowiednio w punktach
odpowiednio w punktach
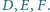 Punkt
Punkt
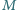 jest
środkiem boku
jest
środkiem boku
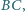 zaś odcinki
zaś odcinki
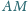 i
i
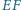 przecinają
się w punkcie
przecinają
się w punkcie
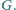 Wykaż, że proste
Wykaż, że proste
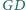 i
i
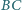 są
prostopadłe.
są
prostopadłe.
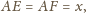
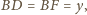
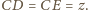 Umieśćmy w
Umieśćmy w
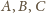 odpowiednio masy
odpowiednio masy
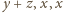 i wyznaczmy środek ciężkości
i wyznaczmy środek ciężkości
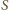 tego układu.
tego układu.
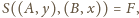
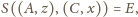 więc
więc
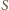 leży na prostej
leży na prostej
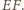 Jednocześnie
Jednocześnie
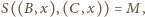 więc
więc
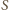 leży też na prostej
leży też na prostej
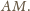 Stąd
Stąd
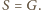
 w punkcie
w punkcie
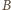 i masę
i masę
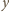 w punkcie
w punkcie
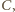 wtedy
wtedy
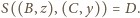 Niech
Niech
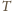 będzie środkiem ciężkości „starych” i „nowych” mas, wtedy
będzie środkiem ciężkości „starych” i „nowych” mas, wtedy
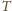 leży na prostej
leży na prostej
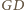 łączącej ich środki ciężkości.
łączącej ich środki ciężkości.
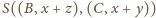 jest
jej spodkiem dla
jest
jej spodkiem dla
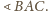 Leży więc na niej punkt
Leży więc na niej punkt
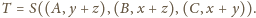 Analogicznie leży on też
na pozostałych dwusiecznych kątów trójkąta, jest zatem środkiem okręgu
wpisanego. Stąd
Analogicznie leży on też
na pozostałych dwusiecznych kątów trójkąta, jest zatem środkiem okręgu
wpisanego. Stąd
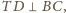 co kończy dowód.
co kończy dowód.
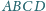 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
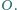 Przekątne
Przekątne
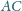 i
i
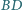 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie
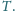 Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
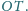
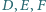 należą odpowiednio do boków
należą odpowiednio do boków
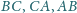 trójkąta
trójkąta
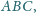 proste
proste
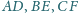 przecinają się w punkcie
przecinają się w punkcie
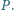 Wykaż,
że
Wykaż,
że
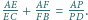
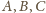 takie masy
takie masy
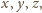 by
by
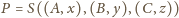 (czy zawsze się da?). Wtedy
(czy zawsze się da?). Wtedy
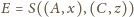 (bo
(bo
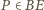 ), zatem
), zatem
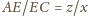 i analogicznie
i analogicznie
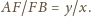
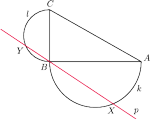
 , na przyprostokątnych
, na przyprostokątnych
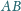 i
i
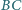 jako na średnicach, zbudowano półokręgi
jako na średnicach, zbudowano półokręgi
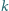 i
i
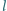 , odpowiednio. Prosta
, odpowiednio. Prosta
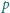 przechodząca przez
punkt
przechodząca przez
punkt
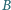 przecina łuki
przecina łuki
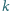 i
i
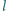 w punktach
w punktach
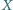 i
i
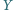 .
Znaleźć położenie tej prostej, dla którego obwód czworokąta
.
Znaleźć położenie tej prostej, dla którego obwód czworokąta
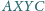 jest maksymalny.
jest maksymalny.
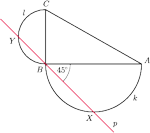
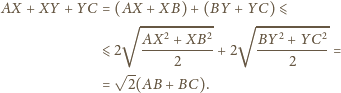
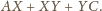 Powyżej zachodzi równość wtedy i tylko wtedy, gdy
Powyżej zachodzi równość wtedy i tylko wtedy, gdy
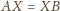 i
i
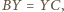 czyli wtedy i tylko wtedy, gdy prosta
czyli wtedy i tylko wtedy, gdy prosta
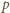 tworzy z półprostą
tworzy z półprostą
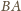 kąt
kąt
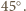
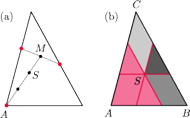
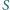 wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
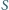 ?
?
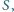 zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
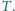 Wykaż, że wszystkie tak wyznaczone
proste
Wykaż, że wszystkie tak wyznaczone
proste
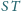 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
 jego wierzchołków, bo obrazem
jego wierzchołków, bo obrazem
 w symetrii względem takiej
osi jest on sam.
w symetrii względem takiej
osi jest on sam.
 trójkąta. Środek ciężkości pozostałych dwóch
much jest w środku
trójkąta. Środek ciężkości pozostałych dwóch
much jest w środku
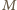 odcinka pomiędzy nimi (
odcinka pomiędzy nimi (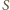 wszystkich much jest na odcinku
wszystkich much jest na odcinku
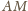 oraz
oraz
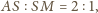 czyli
czyli
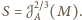 Stąd
Stąd
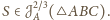
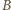 i
i
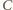 prowadzi do
wniosku, że jedynym możliwym położeniem
prowadzi do
wniosku, że jedynym możliwym położeniem
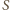 jest środek
ciężkości trójkąta (
jest środek
ciężkości trójkąta (