Zadanie ZM-1456
o zadaniu...
- Publikacja w Delcie: maj 2015
- Publikacja elektroniczna: 30-04-2015
Skonstruuj trójkąt 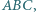 mając dany jego wierzchołek
mając dany jego wierzchołek 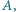 punkt
punkt 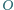 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 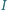 - środek okręgu wpisanego.
- środek okręgu wpisanego.
Czworokąt 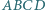 jest wpisany w okrąg
jest wpisany w okrąg 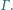 Punkt
Punkt 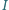 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 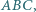 prosta
prosta 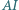 przecina okrąg
przecina okrąg 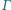 w punkcie
w punkcie 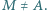 Punkt
Punkt 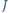 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 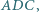 prosta
prosta 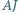 przecina okrąg
przecina okrąg 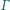 w punkcie
w punkcie 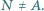 Wykaż, że jeżeli
Wykaż, że jeżeli 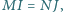 to
to 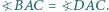
Punkt 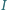 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 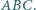 Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie 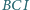 wyznacza na prostych
wyznacza na prostych 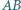 i
i 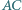 równe cięciwy.
równe cięciwy.
Punkt 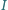 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 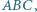 punkt
punkt 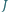 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka 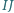 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 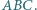
W dany okrąg wpisz trójkąt 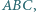 mając dane jego wierzchołki
mając dane jego wierzchołki 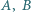 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego.
Okrąg  jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 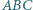 w punkcie
w punkcie 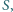 a do boków
a do boków 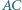 i
i 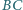 odpowiednio w punktach
odpowiednio w punktach 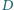 i
i 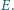 Wykaż, że jeśli
Wykaż, że jeśli 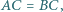 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 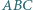 jest środkiem odcinka
jest środkiem odcinka 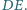
Udowodnij, że w dowolnym trójkącie środkowe przecinają się w jednym punkcie i dzielą w stosunku 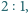 licząc od wierzchołka.
licząc od wierzchołka.
Wykaż, że w każdym trapezie o nierównoległych ramionach punkt przecięcia ich przedłużeń, punkt przecięcia przekątnych i środki podstaw leżą na jednej prostej.
Punkty 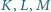 leżą odpowiednio na bokach
leżą odpowiednio na bokach 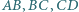 równoległoboku
równoległoboku 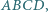 przy czym
przy czym

Proste 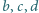 przechodzą odpowiednio przez punkty
przechodzą odpowiednio przez punkty 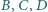 oraz są równoległe odpowiednio do prostych
oraz są równoległe odpowiednio do prostych 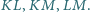 Udowodnij, że proste
Udowodnij, że proste 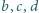 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Każda z przekątnych czworokąta wypukłego dzieli go na trójkąty o równych polach. Wykaż, że ten czworokąt jest równoległobokiem.
Dany jest trójkąt 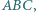 w którym
w którym 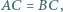 i takie punkty
i takie punkty 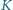 i
i 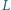 w jego wnętrzu, że
w jego wnętrzu, że 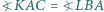 oraz
oraz 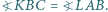 Udowodnij, że punkty
Udowodnij, że punkty 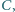
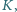
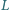 są współliniowe.
są współliniowe.
Dane są liczby dodatnie
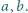 Rozważmy trójkąty prostokątne
Rozważmy trójkąty prostokątne
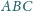 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
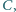 dla których
dla których
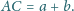 Niech
Niech
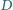 będzie punktem na
będzie punktem na
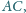 dla którego
dla którego
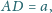
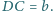 Znaleźć długość boku
Znaleźć długość boku
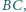 dla
której kąt
dla
której kąt
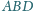 jest maksymalny.
jest maksymalny.
Dany jest kwadrat
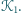 Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
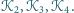 Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
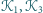 oraz
oraz
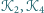 są prostopadłe.
są prostopadłe.